黑马面试篇1-CSDN博客(续集)
六、消息中间件篇
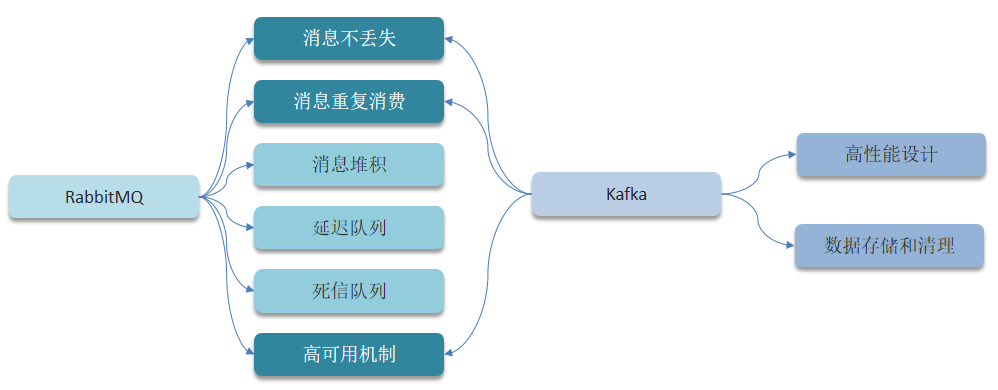
6.1 RabbitMQ
1)使用场景:
- 异步发送(验证码、短信、邮件…)
- MYSQL和Redis , ES之间的数据同步
- 分布式事务
- 削峰填谷
- …
2)RabbitMQ消息的重复消费问题如何解决?
 3)RabbitMQ的高可用机制有了解过吗?
3)RabbitMQ的高可用机制有了解过吗?
- 在生产环境下,使用集群来保证高可用性
- 普通集群、镜像集群、仲裁队列
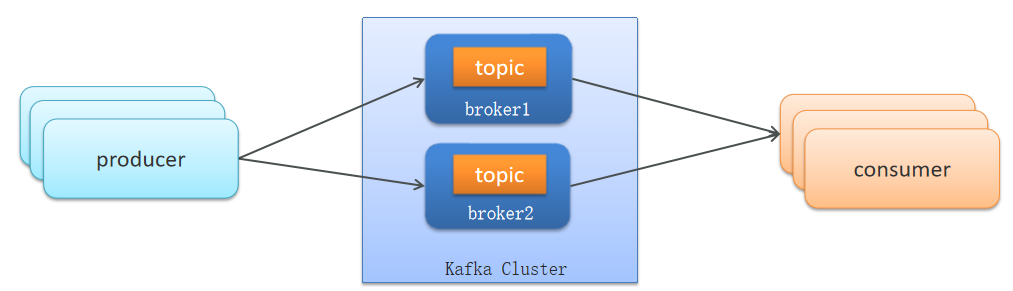
6.2 Kafka
1)Kafka如何保证消息不丢失
使用Kafka在消息的收发过程都会出现消息丢失 , Kafka分别给出了解决方案
- 生产者发送消息到Brocker丢失
- 消息在Brocker中存储丢失
- 消费者从Brocker接收消息丢失

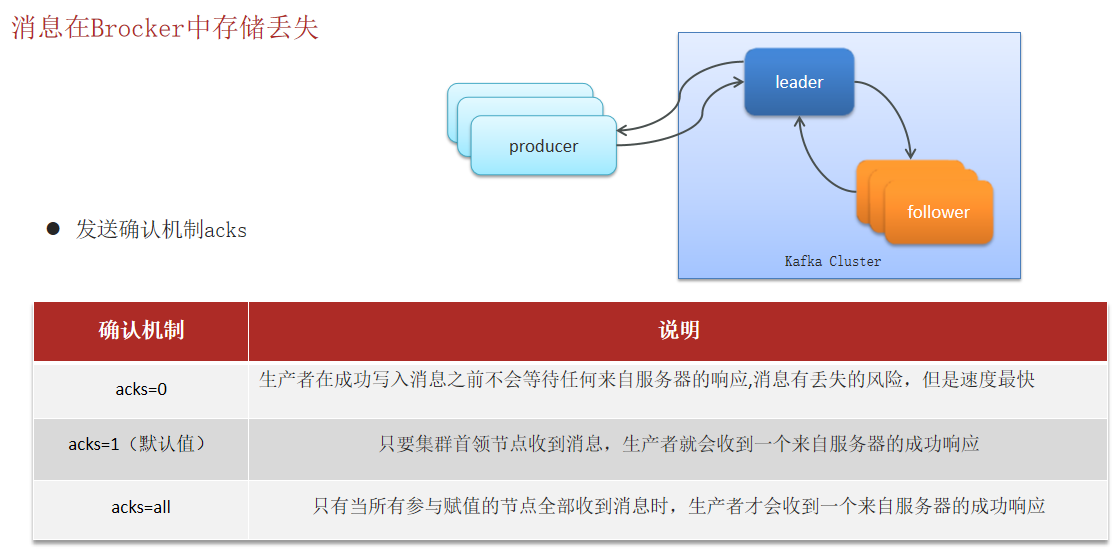

2)重复消费问题Kafka是如何解决的
见上面一张图片左下角。
3)Kafka是如何保证消费的顺序性
应用场景:
- 即时消息中的单对单聊天和群聊,保证发送方消息发送顺序与接收方的顺序一致
- 充值转账两个渠道在同一个时间进行余额变更,短信通知必须要有顺序


4)Kafka的高可用机制有了解过吗?★★★
- 集群模式
- 分区备份机制


5)解释一下复制机制中的 ISR
见上一张图片。
6)Kafka数据清理机制了解吗
- Kafka文件存储机制
- 数据清理机制


7)Kafka中实现高性能的设计有了解吗
Kafka高性能,是多方面协同的结果,包括宏观架构、分布式存储、ISR数据同步、以及高效的利用磁盘、操作系统特性等。主要体现有这么几点:
- 消息分区:不受单台服务器的限制,可以不受限的处理更多的数据
- 顺序读写:磁盘顺序读写,提升读写效率
- 页缓存:把磁盘中的数据缓存到内存中,把对磁盘的访问变为对内存的访问
- 零拷贝:减少上下文切换及数据拷贝
- 消息压缩:减少磁盘IO和网络IO
- 分批发送:将消息打包批量发送,减少网络开销
下图是零拷贝讲解图片:

七、常见集合篇

7.1 算法复杂度分析

一般说的复杂度,都指时间复杂度,因为现在计算机内存空间已经不是瓶颈。
7.2 数据结构
1. 数组



2. 链表
2.1 单向链表
- 链表中的每一个元素称之为结点(Node)
- 物理存储单元上,非连续、非顺序的存储结构
- 单向链表:每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。记录下个结点地址的指针叫作后继指针 next

时间复杂度分析:
查询操作:
- 只有在查询头节点的时候不需要遍历链表,时间复杂度是O(1)
- 查询其他结点需要遍历链表,时间复杂度是O(n)
插入\删除操作:
- 只有在添加和删除头节点的时候不需要遍历链表,时间复杂度是O(1)
- 添加或删除其他结点需要遍历链表找到对应节点后,才能完成新增或删除节点,时间复杂度是O(n)
2.2 双向链表

3. 二叉树
在二叉树中,比较常见的二叉树有:
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 红黑树
二叉搜索树(Binary Search Tree,BST)又名二叉查找树,有序二叉树或者排序二叉树,是二叉树中比较常用的一种类型。二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
总结:
1)什么是二叉树?
- 每个节点最多有两个“叉”,分别是左子节点和右子节点。
- 不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点。
- 二叉树每个节点的左子树和右子树也分别满足二叉树的定义
2)什么是二叉搜索树?
- 二叉搜索树(Binary Search Tree,BST)又名二叉查找树,有序二叉树
- 在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值而右子树节点的值都大于这个节点的值
- 没有键值相等的节点
- 通常情况下二叉树搜索的时间复杂度为O(log n)
- 对于图中这种情况属于最坏的情况,二叉查找树已经退化成了链表,左右子树极度不平衡,此时查找的时间复杂度肯定是O(n)。
4. 红黑树
红黑树(Red Black Tree):也是一种自平衡的二叉搜索树(BST),之前叫做平衡二叉B树(Symmetric Binary B-Tree)。

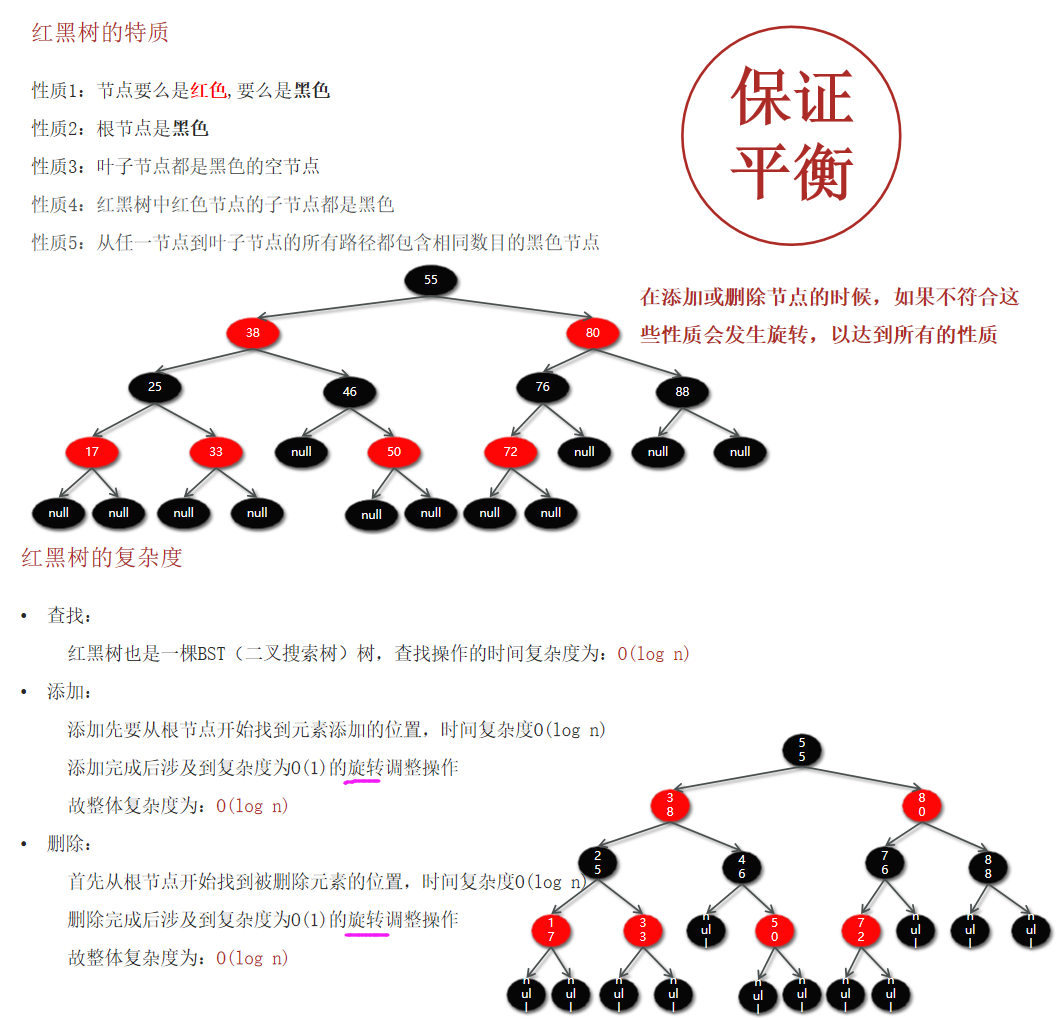
红黑树总结:
- 红黑树(Red Black Tree)也是一种自平衡的二叉搜索树(BST)
- 所有的红黑规则都是希望红黑树能够保证平衡
- 红黑树的时间复杂度:查找、添加、删除都是O(logn)
5. 散列表
在HashMap中的最重要的一个数据结构就是散列表,在散列表中又使用到了红黑树和链表。
1)散列表
散列表(Hash Table)又名哈希表/Hash表,是根据键(Key)直接访问在内存存储位置值(Value)的数据结构,它是由数组演化而来的,利用了数组支持按照下标进行随机访问数据的特性。
2)散列函数
将键(key)映射为数组下标的函数叫做散列函数。可以表示为:hashValue = hash(key)
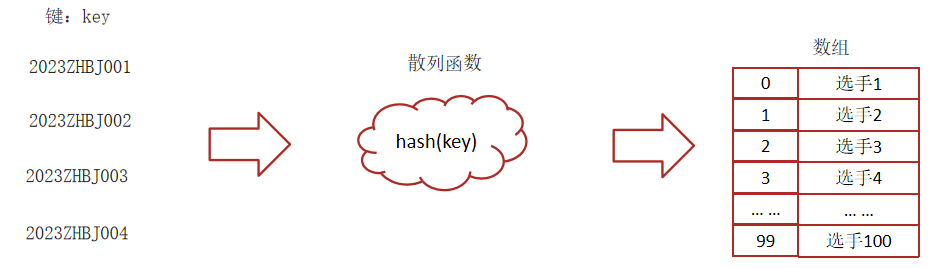
散列函数的基本要求:
- 散列函数计算得到的散列值必须是大于等于0的正整数,因为hashValue需要作为数组的下标。
- 如果key1==key2,那么经过hash后得到的哈希值也必相同即:hash(key1) == hash(key2)
- 如果key1 != key2,那么经过hash后得到的哈希值也必不相同即:hash(key1) != hash(key2)
3)散列冲突
实际的情况下想找一个散列函数能够做到对于不同的key计算得到的散列值都不同几乎是不可能的,即便像著名的MD5,SHA等哈希算法也无法避免这一情况,这就是散列冲突(或者哈希冲突,哈希碰撞,就是指多个key映射到同一个数组下标位置)
4)散列冲突-链表法(拉链)
在散列表中,数组的每个下标位置我们可以称之为桶(bucket)或者槽(slot),每个桶(槽)会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。

5)总结
什么是散列表?
- 散列表(Hash Table)又名哈希表/Hash表
- 根据键(Key)直接访问在内存存储位置值(Value)的数据结构
- 由数组演化而来的,利用了数组支持按照下标进行随机访问数据
散列冲突
- 散列冲突又称哈希冲突,哈希碰撞
- 指多个key映射到同一个数组下标位置
散列冲突-链表法(拉链)
- 数组的每个下标位置称之为桶(bucket)或者槽(slot)
- 每个桶(槽)会对应一条链表
- hash冲突后的元素都放到相同槽位对应的链表中或红黑树中
7.3 ArrayList
ArrayList源码分析(略)
1)ArrayList底层的实现原理(JDK1.8)
2)ArrayList list=new ArrayList(10)中的list扩容几次
答:该语句只是声明和实例了一个 ArrayList,指定了容量为 10,未扩容。
3)如何实现数组和List之间的转换
4)ArrayList和LinkedList的区别★★★

7.4 HashMap
1)说一下HashMap的实现原理?(JDK1.8)★★★

HashMap的jdk1.7和jdk1.8有什么区别?
总结:

2)HashMap的put方法的具体流程★★★

具体流程解答:
put方法流程(代码):
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//判断数组是否未初始化
if ((tab = table) == null || (n = tab.length) == 0)
//如果未初始化,调用resize方法 进行初始化
n = (tab = resize()).length;
//通过 & 运算求出该数据(key)的数组下标并判断该下标位置是否有数据
if ((p = tab[i = (n - 1) & hash]) == null)
//如果没有,直接将数据放在该下标位置
tab[i] = newNode(hash, key, value, null);
//该数组下标有数据的情况
else {
Node<K,V> e; K k;
//判断该位置数据的key和新来的数据是否一样
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//如果一样,证明为修改操作,该节点的数据赋值给e,后边会用到
e = p;
//判断是不是红黑树
else if (p instanceof TreeNode)
//如果是红黑树的话,进行红黑树的操作
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
//新数据和当前数组既不相同,也不是红黑树节点,证明是链表
else {
//遍历链表
for (int binCount = 0; ; ++binCount) {
//判断next节点,如果为空的话,证明遍历到链表尾部了
if ((e = p.next) == null) {
//把新值放入链表尾部
p.next = newNode(hash, key, value, null);
//因为新插入了一条数据,所以判断链表长度是不是大于等于8
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
//如果是,进行转换红黑树操作
treeifyBin(tab, hash);
break;
}
//判断链表当中有数据相同的值,如果一样,证明为修改操作
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
//把下一个节点赋值为当前节点
p = e;
}
}
//判断e是否为空(e值为修改操作存放原数据的变量)
if (e != null) { // existing mapping for key
//不为空的话证明是修改操作,取出老值
V oldValue = e.value;
//一定会执行 onlyIfAbsent传进来的是false
if (!onlyIfAbsent || oldValue == null)
//将新值赋值当前节点
e.value = value;
afterNodeAccess(e);
//返回老值
return oldValue;
}
}
//计数器,计算当前节点的修改次数
++modCount;
//当前数组中的数据数量如果大于扩容阈值
if (++size > threshold)
//进行扩容操作
resize();
//空方法
afterNodeInsertion(evict);
//添加操作时 返回空值
return null;
}3)讲一讲HashMap的扩容机制★★★
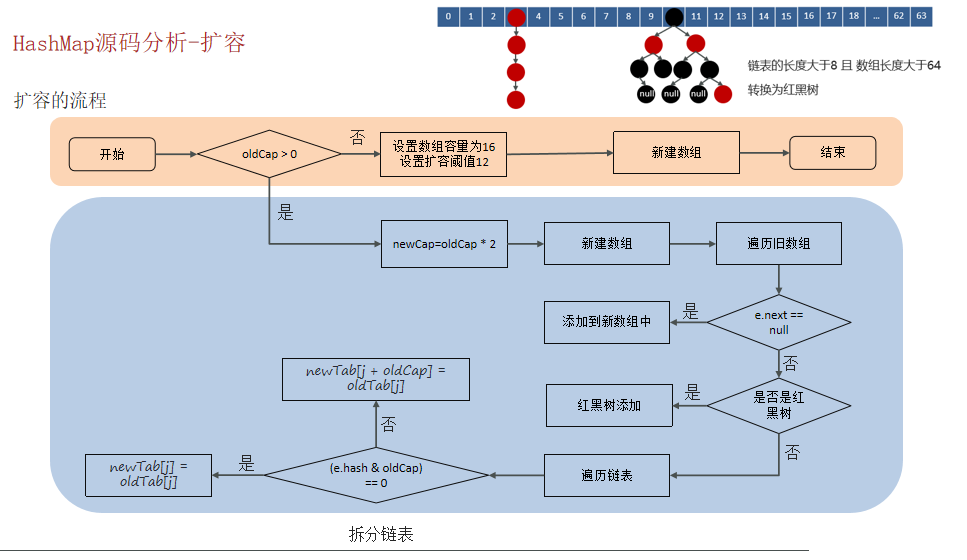
扩容的代码:
//扩容、初始化数组
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
//如果当前数组为null的时候,把oldCap老数组容量设置为0
int oldCap = (oldTab == null) ? 0 : oldTab.length;
//老的扩容阈值
int oldThr = threshold;
int newCap, newThr = 0;
//判断数组容量是否大于0,大于0说明数组已经初始化
if (oldCap > 0) {
//判断当前数组长度是否大于最大数组长度
if (oldCap >= MAXIMUM_CAPACITY) {
//如果是,将扩容阈值直接设置为int类型的最大数值并直接返回
threshold = Integer.MAX_VALUE;
return oldTab;
}
//如果在最大长度范围内,则需要扩容 OldCap << 1等价于oldCap*2
//运算过后判断是不是最大值并且oldCap需要大于16
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold 等价于oldThr*2
}
//如果oldCap<0,但是已经初始化了,像把元素删除完之后的情况,那么它的临界值肯定还存在, 如果是首次初始化,它的临界值则为0
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
//数组未初始化的情况,将阈值和扩容因子都设置为默认值
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
//初始化容量小于16的时候,扩容阈值是没有赋值的
if (newThr == 0) {
//创建阈值
float ft = (float)newCap * loadFactor;
//判断新容量和新阈值是否大于最大容量
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
//计算出来的阈值赋值
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
//根据上边计算得出的容量 创建新的数组
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
//赋值
table = newTab;
//扩容操作,判断不为空证明不是初始化数组
if (oldTab != null) {
//遍历数组
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
//判断当前下标为j的数组如果不为空的话赋值个e,进行下一步操作
if ((e = oldTab[j]) != null) {
//将数组位置置空
oldTab[j] = null;
//判断是否有下个节点
if (e.next == null)
//如果没有,就重新计算在新数组中的下标并放进去
newTab[e.hash & (newCap - 1)] = e;
//有下个节点的情况,并且判断是否已经树化
else if (e instanceof TreeNode)
//进行红黑树的操作
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
//有下个节点的情况,并且没有树化(链表形式)
else {
//比如老数组容量是16,那下标就为0-15
//扩容操作*2,容量就变为32,下标为0-31
//低位:0-15,高位16-31
//定义了四个变量
// 低位头 低位尾
Node<K,V> loHead = null, loTail = null;
// 高位头 高位尾
Node<K,V> hiHead = null, hiTail = null;
//下个节点
Node<K,V> next;
//循环遍历
do {
//取出next节点
next = e.next;
//通过 与操作 计算得出结果为0
if ((e.hash & oldCap) == 0) {
//如果低位尾为null,证明当前数组位置为空,没有任何数据
if (loTail == null)
//将e值放入低位头
loHead = e;
//低位尾不为null,证明已经有数据了
else
//将数据放入next节点
loTail.next = e;
//记录低位尾数据
loTail = e;
}
//通过 与操作 计算得出结果不为0
else {
//如果高位尾为null,证明当前数组位置为空,没有任何数据
if (hiTail == null)
//将e值放入高位头
hiHead = e;
//高位尾不为null,证明已经有数据了
else
//将数据放入next节点
hiTail.next = e;
//记录高位尾数据
hiTail = e;
}
}
//如果e不为空,证明没有到链表尾部,继续执行循环
while ((e = next) != null);
//低位尾如果记录的有数据,是链表
if (loTail != null) {
//将下一个元素置空
loTail.next = null;
//将低位头放入新数组的原下标位置
newTab[j] = loHead;
}
//高位尾如果记录的有数据,是链表
if (hiTail != null) {
//将下一个元素置空
hiTail.next = null;
//将高位头放入新数组的(原下标+原数组容量)位置
newTab[j + oldCap] = hiHead;
}
}
}
}
}
//返回新的数组对象
return newTab;
}4)hashMap的寻址算法
5)为何HashMap的数组长度一定是2的次幂?
hashmap在1.7情况下的多线程死循环问题
HashSet与HashMap的区别
HashTable与HashMap的区别