一、朴素匹配法

S= "abgabcd"

T = "abcd"

假设有两个字符串,要判断字符串T是否在字符串S中出现过，你会怎么做？一般来说我们都是这样，一个一个对比：

#include<iostream>
using namespace std;
int main(){
	string S = "abefabcd";
	string T = "abcd";
	int count = 0;
	int cnt=0;
	cout<<"changduwei:"<<S.length()<<endl;
	for(int i=0,j=0;i<S.length();i++){
		cnt++;
		if(S[i]==T[j]) {
			count ++;
			j++;
			cout<<"count = "<<count<<endl;
			if(count == T.length()) { cout<<"找到一次咯"<<endl; break;}
		}else{
			count = 0;
			cout<<"count = "<<count<<endl;
			j =0 ;
		}
	}
	    
	cout<<"一共找"<<cnt<<"次，才找到"<<endl;
} 

1.2KMP算法的思想 

但是这样会很耗费时间，其实发现子串”abcd"与"abefabcd"的第1，2两位匹配这说明，并且子串中a之后再没有其他a了，这说明主串第2位不可能再和子串的第1位相匹配了，

可以跳过子串第1位和主串第二位比（跳过1->2,2->3,直接从1->3)。所以就有了KMP算法。

2.KMP算法步骤

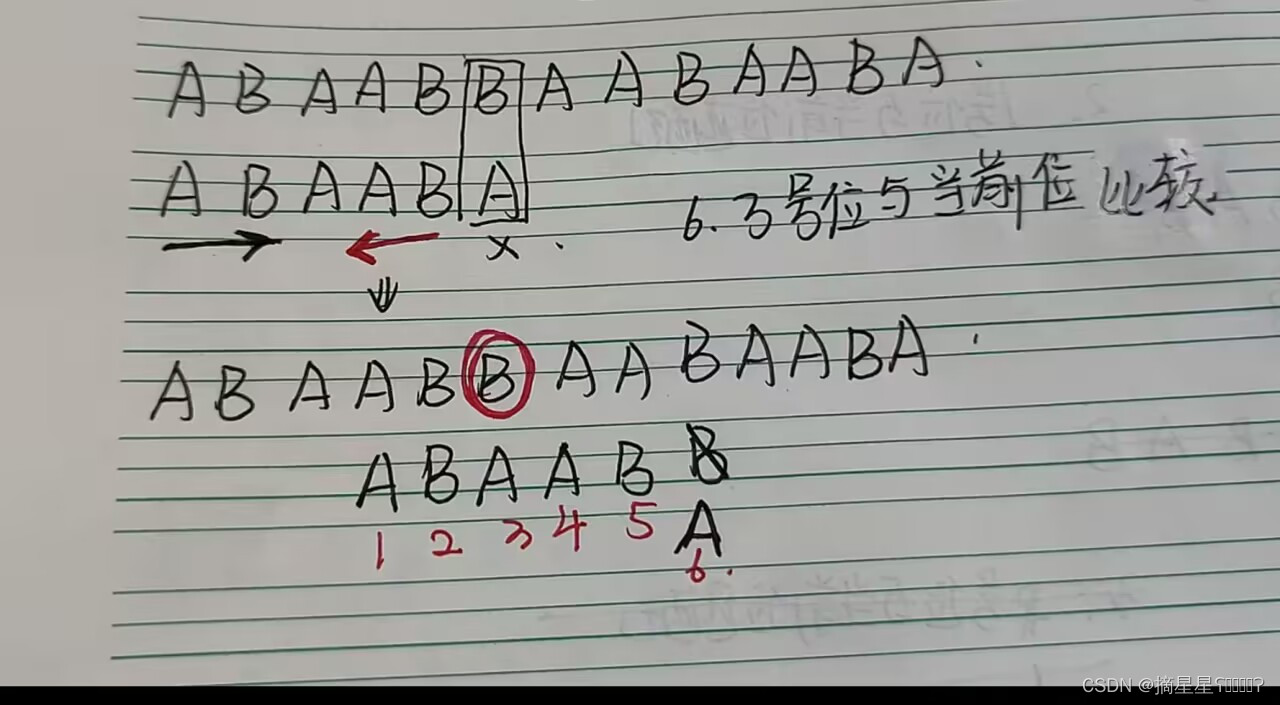
1.找到第一个不匹配的位置 t

发现在第6个位置S中是"B",T中是"A"

2. 在小于t的位置找最长公共前后缀

这句话有三个点，我们剖析一下

2.1 小于t的位置

也就是在前面匹配的串中（暂时把它称为匹配子串），（在这道例题中也就是在1~5的位置：ABABA）找某个东西

2.2 前后缀

一个箭头从匹配子串的最前面开始，另一个箭头从匹配字串的最后一个往前延申，他们是互相奔赴的，找到前后相同的部分

 在这道例题中，上图中红色的A和黑色的A就是一个匹配子串

2.3 最长

但是你发现这个箭头如果继续延伸，还是相同的 

ABA 和 ABA

如果再延长就是：ABAB 和 BABA 不相同

 继续延长箭头：ABABA 和 ABABA  可是这样有意义吗？这不就是同一个串？

所以上图就是最长公共前后缀了

3.前缀移动到后缀的地方

你前面找到最长的相同的部分不就是为了能够最快的跳过没有必要去比的地方吗,所以前缀移动到后缀的位置

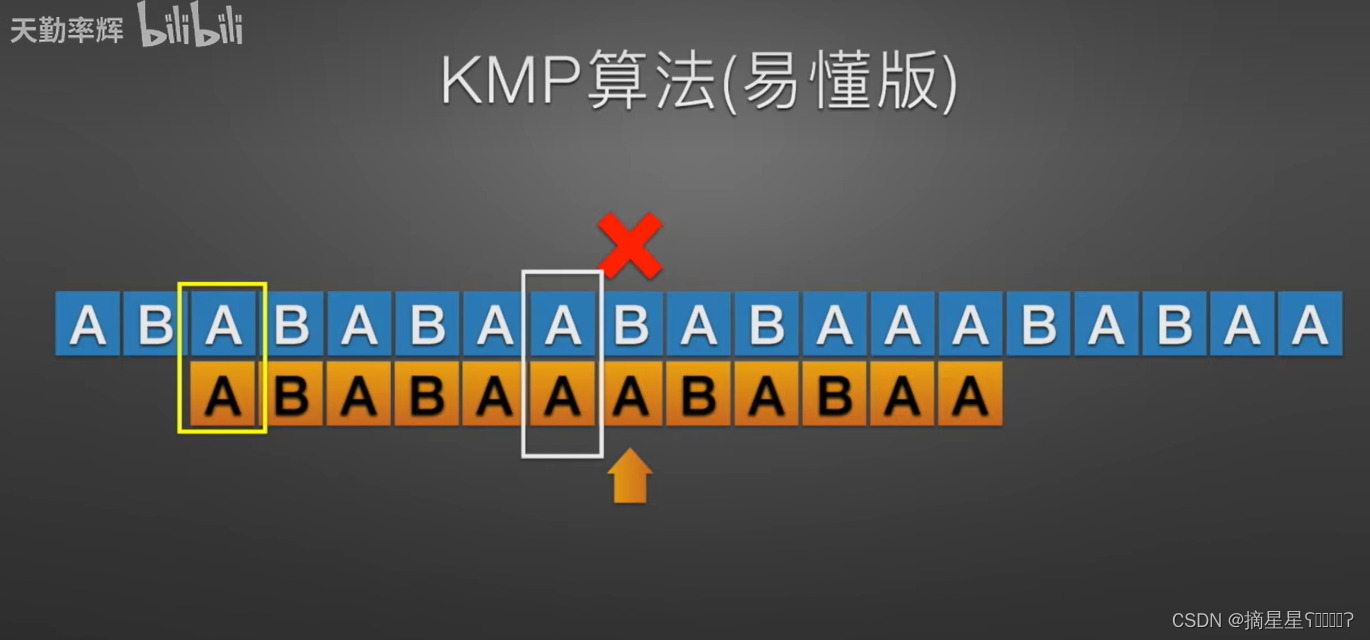
一直重复这个操作，没看懂的去看（跳到8：01讲的就是这里）http://【【天勤考研】KMP算法易懂版】https://www.bilibili.com/video/BV1jb411V78H?vd_source=7f1e3551ae4b557a2f2008705a646502

三、next数组

next 是什么意思，是下一步的意思，所以next数组就是结合KMP算法来告诉你：如果当前位置不匹配，下一步要去找主串中的谁？ 我们来一步步推一下，找找规律

为了方便表达，我们下面把所有不匹配的位称为当前位

例一：如果第一位就不匹配

最长公共前后缀长度=0

那就是1号位和主串下一位去比较，其实就是整个T往后移

 例二：如果第一位匹配，但第二位匹配

最长公共前后缀长度为 = 0

1号位和当前位比较

例三：三号位不匹配

最长公共前后缀长度 = 2，前缀移到后缀的地方

3号位和当前位比较

例四：四号位不匹配

最长公共前后缀长度 = 2，前缀移动到后缀的地方

3号位与当前位比较

例四：五号位不匹配

 

最长公共前后缀长度 = 1，前缀移动到后缀的地方

2号位与当前位比较

我们发现，每次都是 （最长公共前后缀长度 +1）号位与当前位比较

设最长公共前后缀长度为i,那么next数组里存的就是i+1.