一、多重共线性
多重共线性:在多元线性回归时,多个自变量之间存在高度相关关系,时模型估计失真或难以估计准确的情况。
一般地,多元线性回归中自变量间应尽量相互独立。常规模型诊断方法难以检测多重共线性。
1、案例解释
作物产量与生育期内气象条件密切相关,现有某地区10年的作物产量和太阳辐射、温度、降雨的统计数据,据此建立回归模型。
# 产量、生育期内平均温度、平均辐射量的数据集
df<-data.frame(
yield=c(2151,2073,2073,2888,2638,2150,2092,2645,2894,2849),
radn=c(21.0,20.7,23.7,28.8,26.0,22.1,20.8,27.2,28.9,27.4),
temp=c(16.2,15.1,18.2,22.7,21.6,17.8,18.6,22.7,23.9,22.4),
rain=c(218,231,257,278,248,237,201,274,285,290)
)
# 初步探索因变量自变量间关系
library(ggplot2)
library(gridExtra)
# 太阳辐射与产量的关系
p1<-ggplot(data=df,aes(x=radn,y=yield))+geom_point(color="black",shape=3,size=4)
# 温度和产量的关系
p2<-ggplot(data=df,aes(x=temp,y=yield))+geom_point(color="black",shape=3,size=4)
# 降雨和产量的关系
p3<-ggplot(data=df,aes(x=rain,y=yield))+geom_point(color="black",shape=3,size=4)
# 拼接p1、p2、p3
grid.arrange(p1,p2,p3,ncol=3)
# 计算yield与各自变量之间的相关关系
cor(df$yield,df$radn)
cor(df$yield,df$temp)
cor(df$yield,df$rain)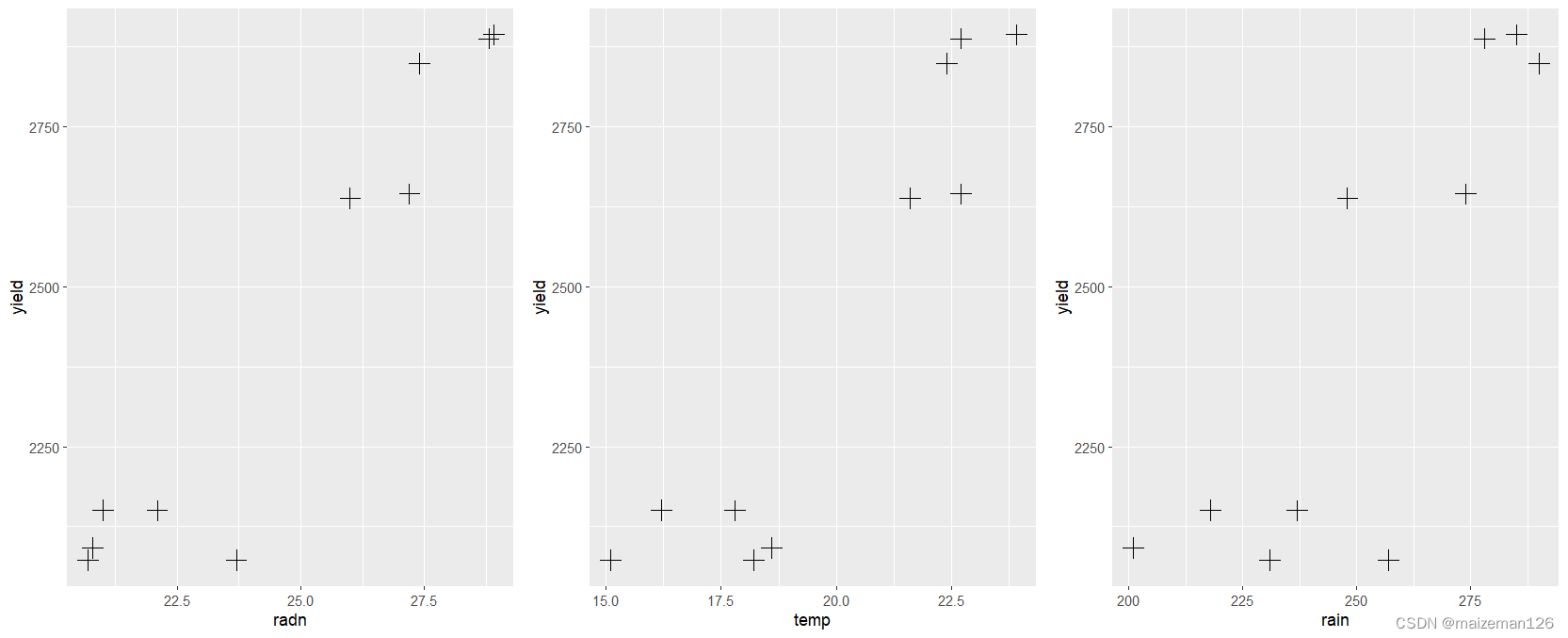

由上图可知:yield变量与radn、temp、rain三个变量具有较高的相关关系。
# 拟合线性回归模型
fit<-lm(yield~radn+temp+rain,data=df)
summary(fit)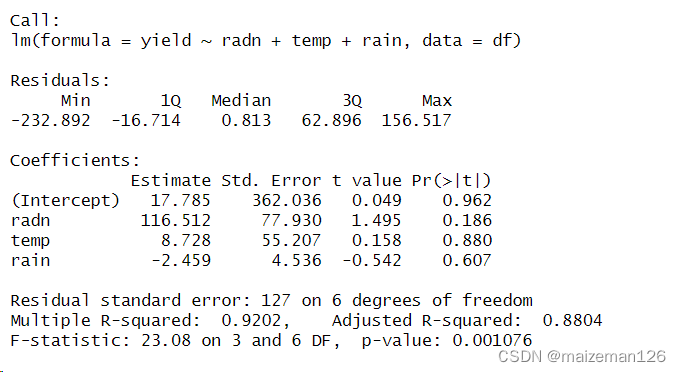
结果:F检验显示回归方程显著存在,且方程的可解释变异达88%;但回归系数t检验则显示3个变量的回归系数均不显著;而且结合前面自变量与因变量的关系图可知3个自变量与因变量是正相关关系,但temp的回归系数却是负的。
这就是多重共线性造成的问题。
2、多重共线性的检验方法
方差扩大因子(variance inflation factor)也成方差膨胀因子,简称VIF。是表征自变量观察值之间复共线性程度的数值。VIF>5表明存在严重的共线性。
# 方差膨胀因子VIF检测多重共线性
fit1<-lm(radn~temp+rain,data=df) # 检验radn的共线性
summary(fit1)
r2<-0.9741
VIF<-1/(1-r2)
VIF
VIF显示radn变量与temp和rain变量存在严重的共线性
也可以使用car包中的vif函数,对拟合的模型进行VIF的计算:

二、逐步回归
逐步回归用于筛选最重要的变量,来建立回归分析的预测或者解释模型。可以解决:当因变量受到大量因素的影响时,建立回归模型,将不可能也没必要考虑的所有影响因素排除在外。
逐步回归实现方法
逐步回归分析是一种AIC信息统计量为准则,通过选择最小的AIC信息统计量,来达到删除或增加变量的目的。
R语言中用于逐步回归分析的是step()函数。
# 产量、生育期内平均温度、平均辐射量的数据集
df<-data.frame(
yield=c(2151,2073,2573,2888,2638,2150,2092,2645,2894,2849),
radn=c(21.0,20.7,23.7,28.8,26.0,22.1,20.8,27.2,28.9,27.4),
temp=c(16.2,15.1,18.2,22.7,21.6,17.8,18.6,22.7,23.9,22.8),
rain=c(218,211,257,288,268,217,201,274,285,290)
)
# 拟合线性回归模型
fit<-lm(yield~radn+temp+rain,data=df)
summary(fit)
# 查看step()函数的帮助文档
?step
# 逐步回归
fit_new<-step(fit)
summary(fit_new)
# 检验两个模型是否存在显著差异
anova(fit,fit_new)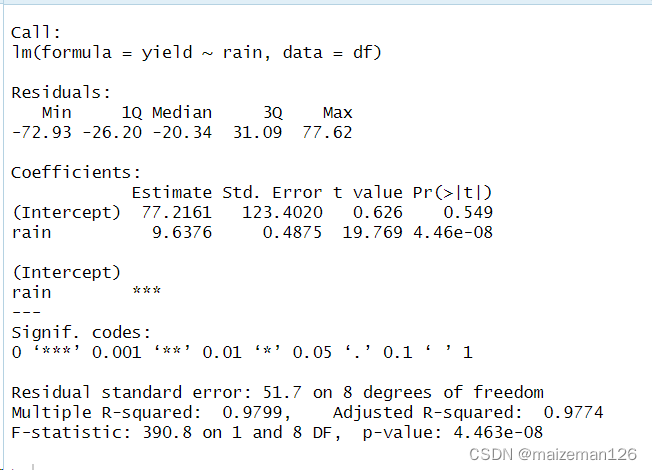
结果:显示temp和radn变量被精简掉了,只保留了rain变量。

结果:显示两个模型间差异不显著。即精简后的模型与原来的模型相差不大。