1、EtherChannel 简介

        EtherChannel （以太网通道）是由 Cisco 公司开发的、应用于交换机之间的多链路捆绑技术。它的基本原理是将两台设备间多条以太网链路捆绑在一起组成一条逻辑链路，形成一个端口通道（PortChannel），从而达到宽带倍增的目的。除了增加带宽，EtherChannel 还可以在多条链路上实现负载均衡。在一跳或多条链路发送故障时，只要还有链路正常工作，流量将转移到其他链路上，整个切换过程在几毫秒内完成，从而起到冗余的作用，增强了网络的稳定性和可靠性。配置 EtherChannel 的链路被视为一个端口参与 STP 运算，因此当 STP 阻塞一条 EtherChannel 链路时，它就阻塞整个 EtherChannel 下的所有物理端口。在 EtherChannel 中，流量在各个链路上的负载分担可以根据源 IP 地址、目的 IP 地址、源 MAC 地址、目的 MAC 地址、源 IP 地址和目的 IP 地址组合、源 MAC 地址和目的 MAC 地址组合等来进行配置

        EtherChannel 可以捆绑 Access 端口、Trunk 端口以及三层端口。一条 EtherChannel 最多可以捆绑 16 个端口，其中最多可以有 8 个端口是活动的。不同类型的交换机支持以太网通道的数量也不相同。在配置 EtherChannel 时，同一组中的全部端口的配置（如 Trunk封装。速率和双工模式）必须相同，因此 Trunk 端口 和 Access 端口是不能捆绑在一起的。

2、PAgP 和 LACP 协商规律

        EtherChannel 可以手工配置，也可以自动协商。目前有 2 个 EtherChannel 协商协议；端口聚合协议（Port Aggregation Protocol，PAgP）和链路聚合控制协议（Link Aggregation Control Protocol，LACP），PAgP 是 Cisco 私有协议，而 LACP 是国际标准。这 2 个协议各自有不同的工作模式，不同模式组合会有不同的协商结果。PAgP 协商规律如表 1 所示，LACP 协商规律如表 2 所示，两个表中的 ON 表示管理员手工配置了 EtherChannel。

表 1 PAgP 协商规律

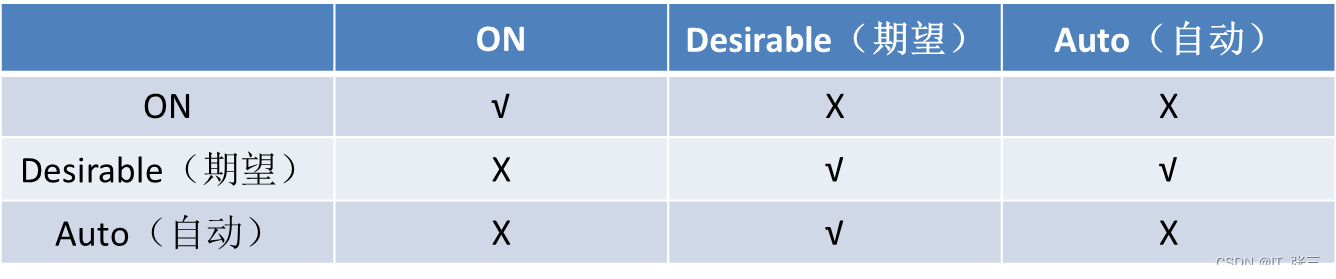
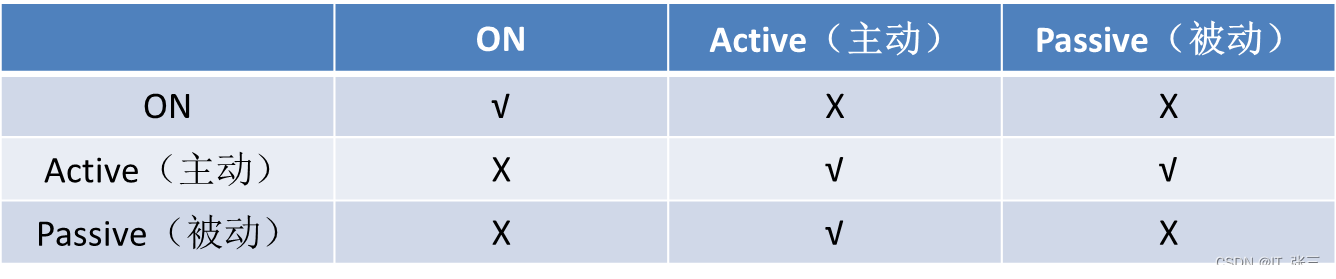
表 2 LACP 协商规律