【人工智能基础】聚类实验分析

实验环境：anaconda、jupyter notebook、spyder

实现用到的类库：numpy、matplotlib、scikit-learn

k均值聚类（K-MEANS）

k均值聚类的原理：

选定k个聚类中心
把数据集中距离聚类中心i最近的点都归属到一个簇
根据每个簇中的点计算出新的聚类中心
如果聚类中心没有发生移动，则聚类完成，否则重复2，3，4

一、根据k均值聚类的原理，尝试自己实现

k均值实现类

import math
import numpy as np
import matplotlib.pyplot as plt

class KMeans:
    def __init__(self):
        # 聚类的每一步
        self.clustering_step = []

    def train(self,data, num_clusters):
        self.data = data
        self.num_clusters = num_clusters

        count = data.shape[0]
        # 获取初始聚类中心
        self.center = self.init_clustering_center()
        # 存储原始状态
        self.clustering_step.append([np.copy([self.data]),np.copy(self.center)])

        # 聚类一次
        new_center,cluster = self.updata_clustering_center()

        # 如果聚类中心的位置产生了移动继续聚类
        while not KMeans.is_equal(new_center, self.center):
            self.center = new_center
            temp = [cluster,np.copy(self.center)]
            self.clustering_step.append(temp)
            new_center,cluster = self.updata_clustering_center()



    @staticmethod
    def is_equal(array1, array2):
        for i in range(len(array1)):
            if (array1[i][0] - array2[i][0])**2 > 1e-10 and (array1[i][1] - array2[i][1])**2 > 1e-10:
                return False
        return True


    def init_clustering_center(self):
        """
        初始化聚类中心
        洗牌数组后随机取k个数值
        """
        return self.data[np.random.permutation(self.data.shape[0])][:self.num_clusters]


    def updata_clustering_center(self):
        '''
        更新聚类中心
        '''
        # 记录每组的点
        cluster = []
        for _ in range(self.num_clusters):
            cluster.append([])

        for d in self.data:
            distance = []
            # 计算每个样本点到假定聚类中心的欧式距离
            for c in self.center:
                distance.append(np.sum((d - c))**2)
            # 每个点分配到最近的聚类中心
            min_index = np.argmin(distance)
            cluster[min_index].append(d)
            new_center = []
            # 计算新聚类中心的位置
            for c in cluster:
                if len(c) == 0:
                    new_center.append([0,0])
                    continue
                new_center.append(np.sum(c,axis=0) / len(c))
        cluster = [np.array(x) for x in cluster]
        return new_center,cluster



    def show_step(self,row):
        '''
        绘制聚类过程
        '''
        color = ['r','b','y']

        step = len(self.clustering_step)
        col = math.ceil(step / row)
        plt.figure(figsize=(row * 6, col * 5))

        for i in range(step):
            plt.subplot(row,math.ceil(step / row), i + 1)
            current_step = self.clustering_step[i]
            group = current_step[0]
            center = current_step[1]
            for g in group:
                plt.scatter(g[:,0], g[:,1])
            plt.scatter(center[:,0], center[:,1] ,c='k',marker='x')
            plt.title(label='clustering:{}'.format(i+1))

        plt.legend()
        plt.show()

2.运行k均值算法

这里使用的数据集是鸢尾花数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

from my_work.k_means import KMeans

iris = datasets.load_iris()
data = iris.data
class_ = iris.target
print(class_)

x_axis = 2
y_axis = 3

x1 = data[:,x_axis]
x2 = data[:,y_axis]


# 绘制原始的图
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
for iris_type in np.unique(class_):
    plt.scatter(x1[class_==iris_type],
                x2[class_==iris_type],
                label=iris_type)
plt.subplot(1,2,2)
plt.scatter(x1, x2)
plt.legend()
plt.show()

# 绘制经过kmeans算法得到的训练过程
x_train = np.c_[x1,x2]
kmeans = KMeans()
num_clusters = np.unique(class_).shape[0]
kmeans.train(x_train, num_clusters)
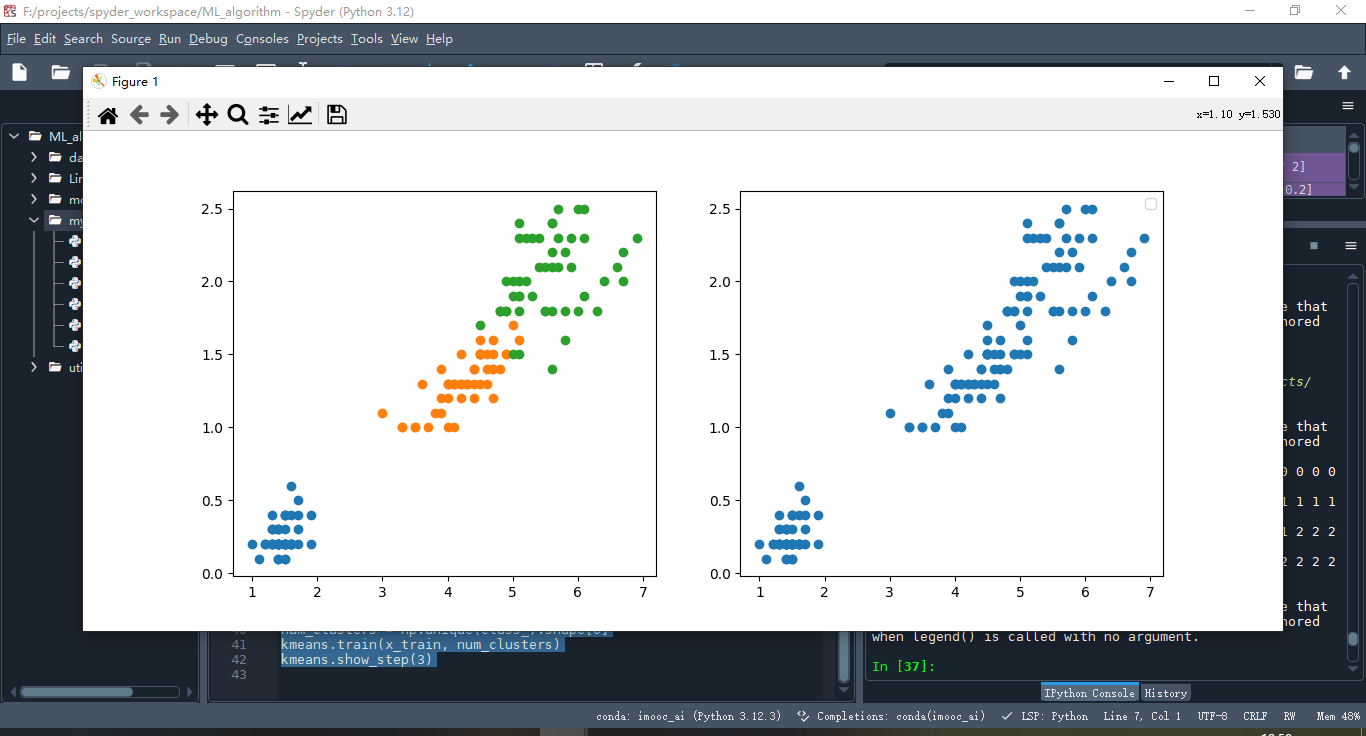
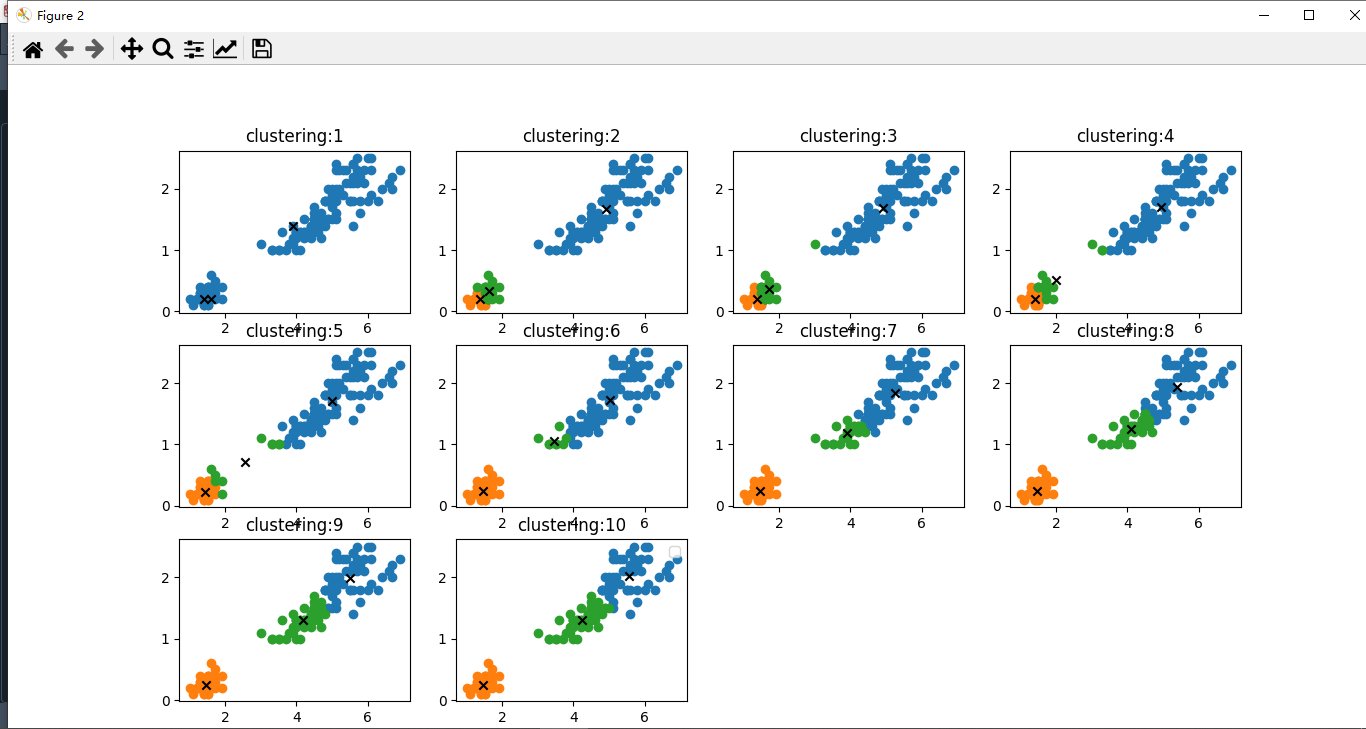
kmeans.show_step(3)

3.结果

我们自己实现的算法能够完成k均值分类的任务

鸢尾花数据集真实聚类

鸢尾花数据集k均值算法聚类

二、scikit-learn提供的kmeans算法

1.实验准备

import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)

2.初始化样本数据集

创建数据集

# 引入椭圆
from sklearn.datasets import make_blobs

# 指定五个中心
blob_centers = np.array(
    [[0.2,2.3],
    [-1.5,2.3],
    [-2.8,1.8],
    [-2.8,2.8],
    [-2.8,1.3]]
)

blob_std = np.array([0.4,0.3,0.1,0.1,0.1])

x,y = make_blobs(
    # 样本个数
    n_samples=2000,
    # 中心点
    centers=blob_centers,
    # 发散程度
    cluster_std=blob_std,
    random_state=7
)

绘制数据集

# 绘图函数
def plot_clusters(x, y= None):
    plt.scatter(x[:,0],x[:,1],c=y,s=1)
    plt.xlabel('$x_1$',fontsize=14)
    plt.ylabel('$x_2$',fontsize=14)
# 绘制图像    
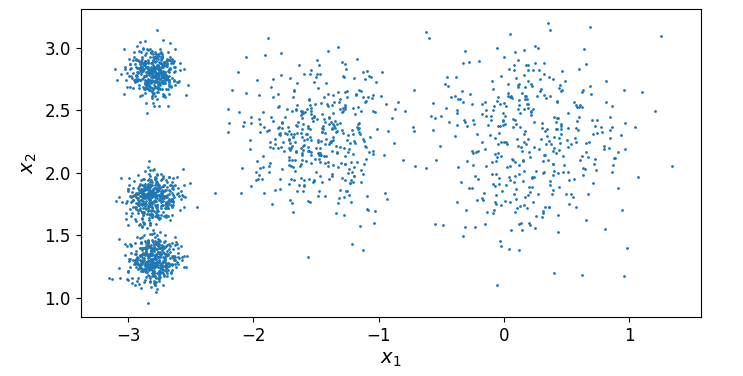
plt.figure(figsize=(8,4))
plot_clusters(x)
plt.show()

我们创建了五个聚类中心的数据集

椭圆数据集

3.使用kmeans算法实现聚类

实现聚类

from sklearn.cluster import KMeans
# 聚类中心个数
k = 5
kmeans = KMeans(n_clusters = k, random_state=42,n_init='auto')
# 打印每个点所属的的聚类
print(kmeans.labels_)
print(kmeans.fit_predict(x))
# 打印聚类中心的位置
print(kmeans.cluster_centers_)
# 预测这些点所属的聚类中心
x_new = np.array([[0,2],[3,2],[-3,-3],[-3,2.5]])
print(kmeans.predict(x_new))

绘制函数

def plot_data(x):
    """
    绘制入参的图像
    """
    plt.plot(x[:,0],x[:,1],'k.',markersize=2)

def plot_centroids(centroids, weights=None, circle_color='w',cross_color='k'):
    """
    绘制中心点
    """
    if weights is not None:
        centroids = centroids[weights > weights.max() / 10]
    plt.scatter(centroids[:,0],
                centroids[:,1],
                marker='o',
                s=30,
                linewidths=8, 
                color=circle_color, 
                zorder=10,
                alpha=0.9)
    plt.scatter(centroids[:,0],
                centroids[:,1],
                marker='x',
                s=50,
                linewidths=1, 
                color=cross_color, 
                zorder=11,
                alpha=1)

def plot_decision_boundaries(clusterer, x, resolution=100, show_centroids=True,
                            show_xlabels=True,show_ylabels=True):
    """
    绘制聚类器对参数x的聚类结果
    """
    mins = x.min(axis=0) - 0.1
    maxs = x.max(axis=0) + 0.1
    xx,yy = np.meshgrid(np.linspace(mins[0],maxs[0],resolution),
                        np.linspace(mins[1],maxs[1],resolution))
    z = clusterer.predict(np.c_[xx.ravel(),yy.ravel()])
    z = z.reshape(xx.shape)
    plt.contourf(z, extent=(mins[0],maxs[0],mins[1],maxs[1]), cmap='Pastel2')
    plt.contour(z, extent=(mins[0],maxs[0],mins[1],maxs[1]),linewidths=1,colors='k')
    plot_data(x)
    if show_centroids:
        plot_centroids(clusterer.cluster_centers_)
    if show_xlabels:
        plt.xlabel('$x_1$',fontsize=14)
    else:
        plt.tick_params(labelbottom='off')
    if show_ylabels:
        plt.ylabel('$x_2$',fontsize=14,rotation=0)
    else:
        plt.tick_params(labelleft='off')

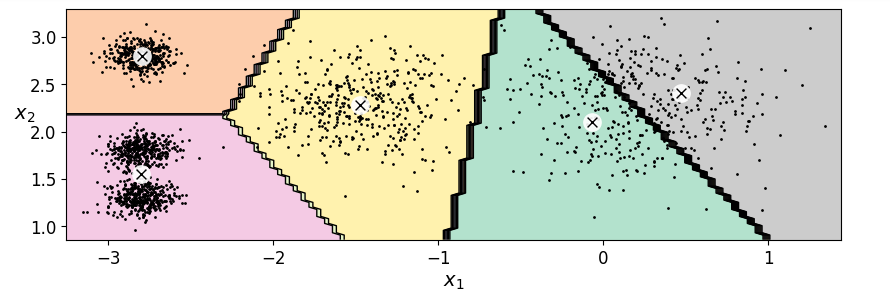
绘制聚类结果

plt.figure(figsize=(10,3))
plot_decision_boundaries(kmeans,x)
plt.show()

kmeans聚类结果

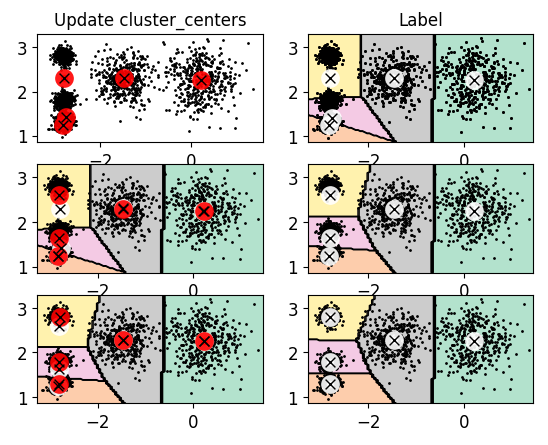
三、聚类过程

创建三个kmeans对象，分别进行1，2，3次迭代聚类

kmeans__iter1 = KMeans(n_clusters = 5, init='random',n_init=1, max_iter=1,random_state=1)
kmeans__iter1.fit(x)
kmeans__iter2 = KMeans(n_clusters = 5, init='random',n_init=1, max_iter=2,random_state=1)
kmeans__iter2.fit(x)
kmeans__iter3  = KMeans(n_clusters = 5, init='random',n_init=1, max_iter=3,random_state=1)
kmeans__iter3.fit(x)

绘制图像

plt.figure(figure=(10,8))

plt.subplot(321)
plot_data(x)
plot_centroids(kmeans__iter1.cluster_centers_,circle_color='r',cross_color='k')
plt.title('Update cluster_centers')

plt.subplot(322)
plot_data(x)
plot_decision_boundaries(kmeans__iter1,x,show_xlabels=False,show_ylabels=False)
plt.title('Label')

plt.subplot(323)
plot_decision_boundaries(kmeans__iter1,x,show_xlabels=False,show_ylabels=False)
plot_centroids(kmeans__iter2.cluster_centers_,circle_color='r',cross_color='k')

plt.subplot(324)
plot_decision_boundaries(kmeans__iter2,x,show_xlabels=False,show_ylabels=False)


plt.subplot(325)
plot_decision_boundaries(kmeans__iter2,x,show_xlabels=False,show_ylabels=False)
plot_centroids(kmeans__iter3.cluster_centers_,circle_color='r',cross_color='k')

plt.subplot(326)
plot_decision_boundaries(kmeans__iter3,x,show_xlabels=False,show_ylabels=False)

plt.show()

kmeans聚类过程

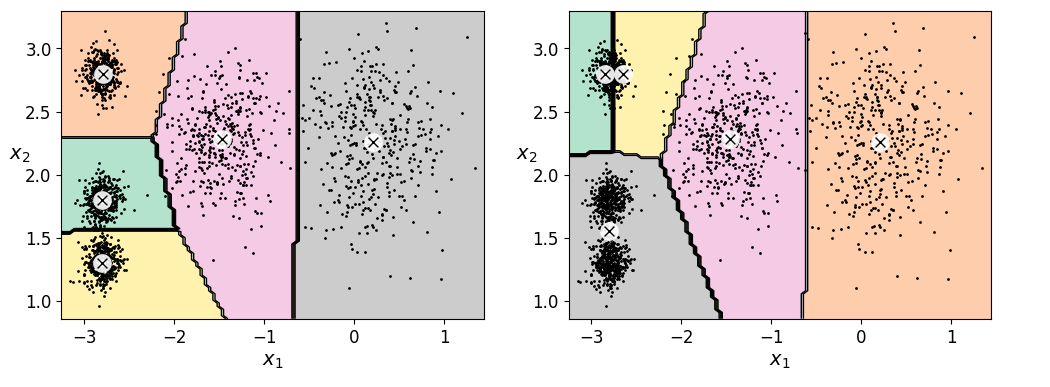
四、kmeans的不稳定性

kmeans初始的聚类中心不同可能会得到不同的聚类结果

def plot_clusterer_comparison(c1,c2,x):
    c1.fit(x)
    c2.fit(x)

    plt.figure(figsize=(12,4))
    plt.subplot(121)
    plot_decision_boundaries(c1,x)
    plt.subplot(122)
    plot_decision_boundaries(c2,x)
c1 = KMeans(n_clusters = 5, init='random',n_init=1, random_state=11)
c2 = KMeans(n_clusters = 5, init='random',n_init=1, random_state=49)
plot_clusterer_comparison(c1,c2,x)

kmeans不稳定性

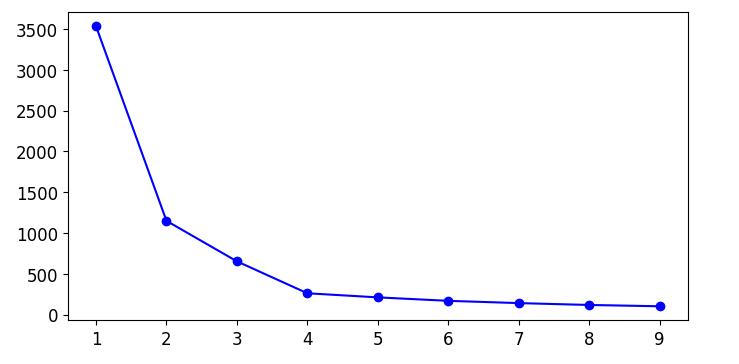
五、寻找合适的k值（只是参考）

inertia指标

inertia指标：每个样本与其质心的距离使用kmeans对象.inertia_来查看

根据inertia指标的转折点

# 获得聚类数为1~10的10个kmeans对象
kmeans_per_k = [KMeans(n_clusters = k).fit(x) for k in range(1,10)]
# 获得这些kmeans对象的inertia指标
interias = [model.inertia_ for model in kmeans_per_k]
# 绘制inertia指标变化图
plt.figure(figsize=(8,4))
plt.plot(range(1,10),interias,'bo-')
plt.show()

根据这个图像，我们认为最佳的聚类数应该是4，实际应该是5，这个指标做为参考，不一定是最优结果

inertia指标变化图

根据轮廓系数

轮廓系数规定参数：

ai：计算样本i到同簇其他样本的平均距离。簇内不相似度
bi：计算样本到其他某簇Cj的所有样本的平均距离bij。簇间不相似度
si = (bi - ai) / max{ai.bi}

由此我们可以知道：

si越接近1，说明样本i聚类合理
si接近-1，说明样本i更应该分到别的簇
si近似为0，说明样本在两个簇的边界

from sklearn.metrics import silhouette_score
scores = [silhouette_score(x, model.labels_) for model in kmeans_per_k[1:]]
plt.figure(figsize=(8,4))
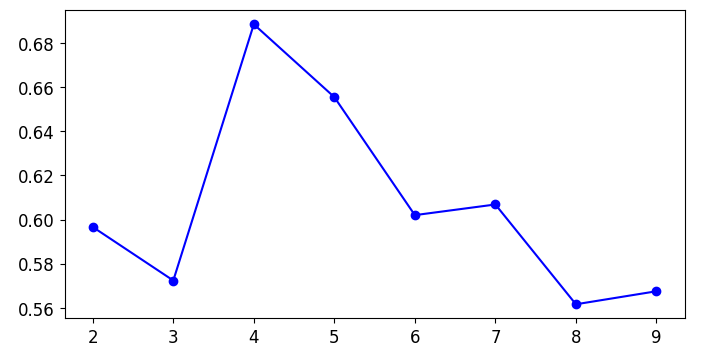
plt.plot(range(2,10),scores,'bo-')
plt.show()

根据这个图像，我们认为最佳的聚类数应该是4，实际应该是5，这个指标做为参考，不一定是最优结果

轮廓系数变化图

六、kmeans进行图像分割

使用的图像是，把这个图像放在python脚本文件相同目录下

ladybug

from matplotlib.image import imread
# 读入图像
image = imread('ladybug.png')
# 图像本身是三维数据，需要转换成二维进行处理
x = image.reshape(-1,3)
# 存储图像分类结果
segmented_imgs = []
# 表示颜色的种类数量
n_colors = (10,8,6,4,2)
# 按不同和的颜色种类数量训练模型
for n_clusters in n_colors:
    kmeans = KMeans(n_clusters=n_clusters, random_state=42).fit(x)
    # 用聚类中心的颜色来替代整个簇的颜色
    segmented_img = kmeans.cluster_centers_[kmeans.labels_]
    segmented_imgs.append(segmented_img.reshape(image.shape))
#绘制图像
plt.figure(figsize=(10,5))
plt.subplot(231)
plt.imshow(image)
plt.title('original image')
for idx,n_clusters in enumerate(n_colors):
    plt.subplot(232+idx)
    plt.imshow(segmented_imgs[idx])
    plt.title('{}colors'.format(n_clusters))
plt.show()

kmeans图像分割

DBSCAN

DBSCAN算法：找到图中的核心对象，把核心对象与核心对象ε-邻域中的点都聚为一类，若ε-邻域中的点也是核心对象，则继续本类的聚类

核心对象：若某个点的密度达到算法设定的阈值，则其为核心点（r邻域内点的数量不小于minPts）
ε-邻域的距离阈值：设定的半径r
直接密度可达：若某点p在点q 的r邻域内，且q是核心点，则称p-q直接密度可达
密度可达：若有一个点的序列q0、q1……qk，对任意qi-qi-1是直接密度可达的，则q0到qk密度可达（直接密度可达的传播）

创建数据集

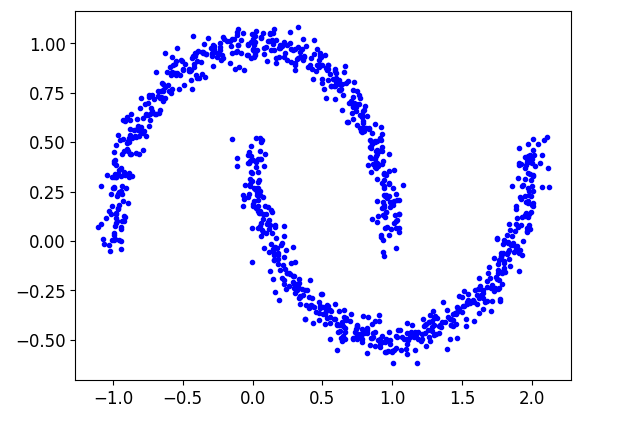
from sklearn.datasets import make_moons
x, y = make_moons(n_samples=1000,noise=0.05,random_state=42)
plt.plot(x[:,0],x[:,1],'b.')
plt.show()

这个数据集不适合使用kmeans算法进行聚类

DBSCAN数据集

执行聚类学习

from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.05,min_samples=5)
dbscan.fit(x)

dbscan2 = DBSCAN(eps=0.2,min_samples=5)
dbscan2.fit(x)

图像绘制函数

def plot_dbscan(dbscan,x,size,show_xlabels=True, show_ylabels=True):
    core_mask = np.zeros_like(dbscan.labels_,dtype=bool)
    core_mask[dbscan.core_sample_indices_]=True
    anomalies_mask = dbscan.labels_ == -1
    non_core_mask = ~(core_mask | anomalies_mask)

    cores=dbscan.components_
    anomalies=x[anomalies_mask]
    non_cores=x[non_core_mask]

    plt.scatter(cores[:,0],cores[:,1],
               c=dbscan.labels_[core_mask], marker='o',s=size,cmap='Paired')
    plt.scatter(cores[:,0],cores[:,1],marker='*',s=20,c=dbscan.labels_[core_mask])
    plt.scatter(non_cores[:,0],non_cores[:,1],c=dbscan.labels_[non_core_mask],marker='.')
    if show_xlabels:
        plt.xlabel('$x_1$',fontsize=14)
    else:
        plt.tick_params(labelbottom='off')
    if show_ylabels:
        plt.ylabel('$x_2$',fontsize=14,rotation=0)
    else:
        plt.tick_params(labelleft='off')
    plt.title('eps={:.2f}, min_samples={}'.format(dbscan.eps, dbscan.min_samples),fontsize=14)

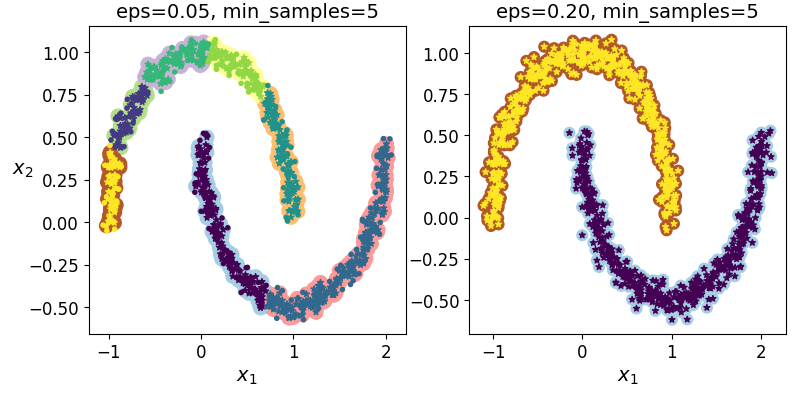
绘制两个DBSCAN聚类器的图像

plt.figure(figsize=(9,4))

plt.subplot(121)
plot_dbscan(dbscan,x,size=100)

plt.subplot(122)
plot_dbscan(dbscan2,x,size=60,show_ylabels=False)

plt.show()

DBSCAN聚类结果