概述

Min_25是日本一个ACM选手的ID，这个筛法是他发明的，所以称之为Min_25筛。它能在亚线性复杂度求出一类积性函数的 $f$ 的前缀和，前提 是这个积性函数在质数和质数的幂位置的函数值比较好求。借助埃拉托色尼筛的思想 将原问题转化成与质因子相似的子问题，从而得到一个递推式，达到快速求解的效果。

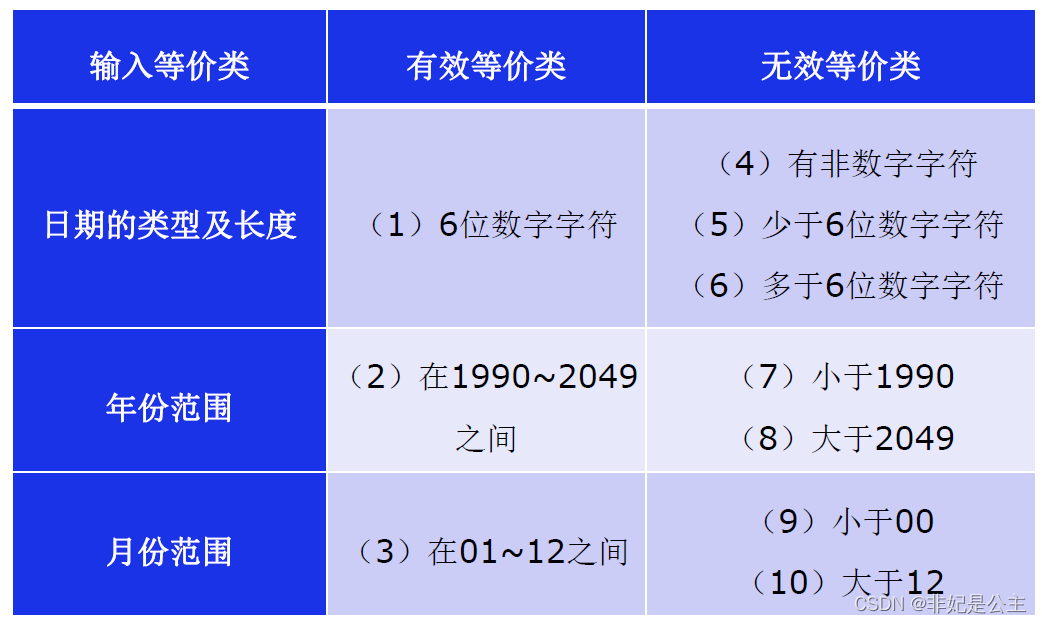
对比其他算法

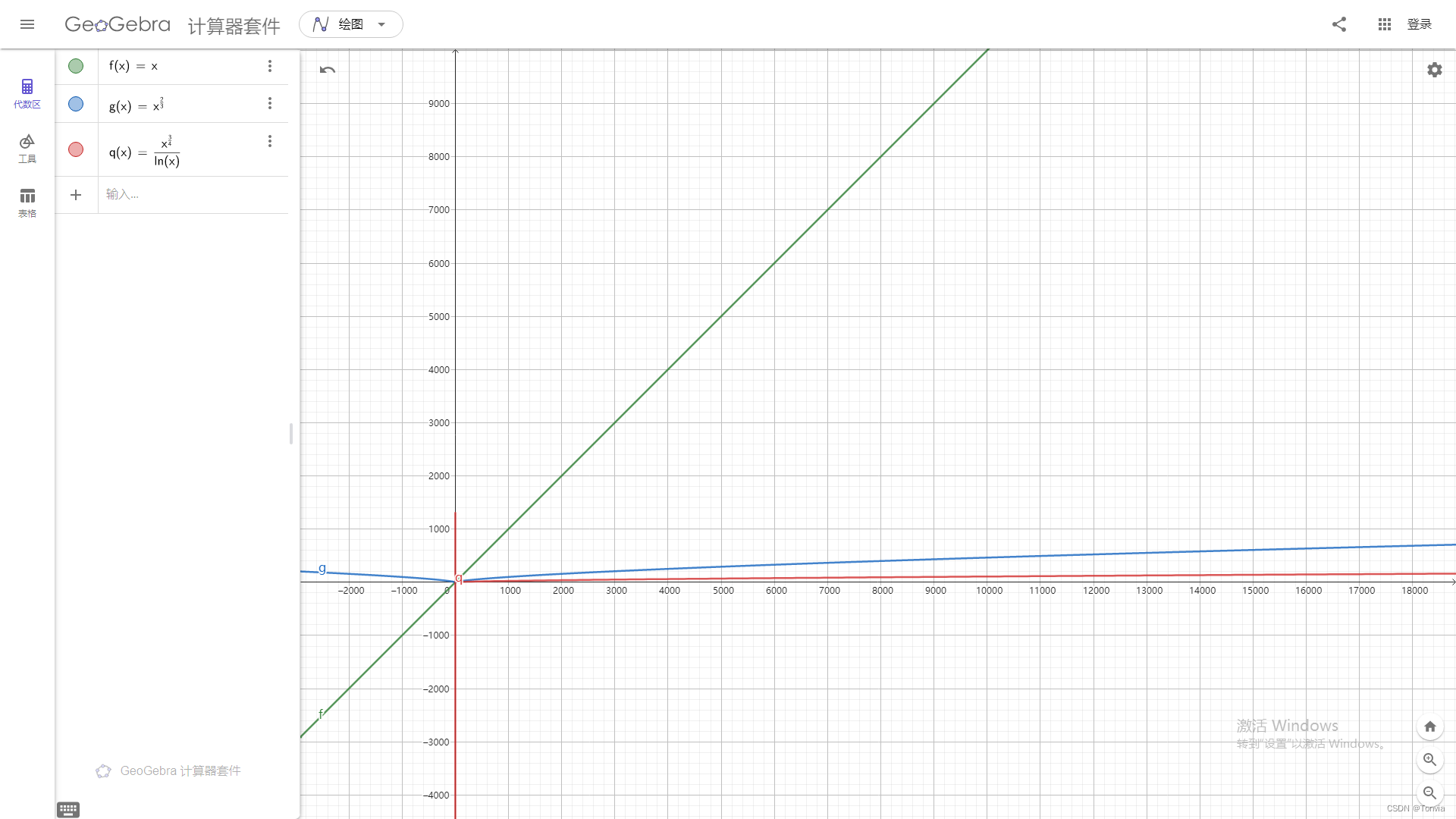
(绿色为 $O(n)$，红色为Min_25筛，蓝色为杜教筛)
可以发现，Min_25时间复杂度尽管只快了杜教筛常数级，但终究是快的

因为Min_25筛不像杜教筛那样需要构造，所以Min_25筛的适用范围更加的广泛。

算法原理

为了方便描述，我们定义一些符号。

• 设我们的问题是 $F(n)=\sum _{i=1}^{n}f(i)$ ;假定 $f$ 是一个完全积性函数。

• 设 $minp(i)$ 表示 $i$ 的最小质因子。

• 设 $p{r}_k$ 表示第 $k$ 个质数。

• 设 $|pr(n)|$ 表示 $n$ 以内的质数个数。

• 设 $g(n,i)$ 表示在埃拉托色尼筛中，前 $i$ 个筛完后，剩下的数的 $f$ 值之和。即质数和最小质因子大于 $p{r}_i$ 的合数。

则有
$$g(n,i)=\sum _{(j\in Prime)\vee (minp(j)>p{r}_i)}f(j)$$
于是可知 $g(n,|pr(n)|)$ 表示的是做完埃氏筛之后，$n$ 以内所有质数 $f$ 值之和，$g(p{r}_k,k)$ 表示的是 前 $k$ 个质数的 $f$ 值之和（含义差不多）

发现可以用如下的递推式求出 $g(n,i)$ 的值。
$$g(n,i)=\{\begin{array}{ll}g(n,i-1),& p{r}_i^2>n\\ g(n,i-1)-f(p{r}_i)\times (g(\lfloor \frac{n}{p{r}_i}\rfloor ,i-1)-g(p{r}_{i-1},i-1))& p{r}_i^2\le n\end{array}$$

第一行的式子很容易理解，回忆埃氏筛的方法，$n$ 第一次一定是被最小质因子筛掉。$p{r}_i^2>n$，那么 $p{r}_i$ 不会筛掉任何数，便不会产生任何贡献。

但是第二个式子就比较难理解了，我也花了十几分钟的时间才彻底明白。
首先， $g(n,i)$ 较 $g(n,i-1)$ 而言，就是以 $p{r}_i$ 为最小质因子的数被筛掉了，那么减去的就应该是 $n$ 以内以 $p{r}_i$ 为最小质因子的数。

$g(\lfloor \frac{n}{p{r}_i}\rfloor ,i-1)$ ，除去了一个 $p{r}_i$ ，得到的 $\lfloor \frac{n}{p{r}_i}\rfloor$ 是 $n$ 以内以 $p{r}_i$ 为质因子能筛掉的数中，可能出现的除 $p{r}_i$ 以外倍数的最大值。
所以 $g(\lfloor \frac{n}{p{r}_i}\rfloor ,i-1)$ 得到的是 $\lfloor \frac{n}{p{r}_i}\rfloor$ 以内 $minp(x)\ge p{r}_{i-1}$ 的 $f$ 值和 $\sum _{j\in Prime}^{p{r}_{i-1}}f(j)$ 之和。

但是埃氏筛时只有满足 $minp(x)\ge p{r}_{i-1}$ 的才会被筛掉啊，所以得把 $\sum _{j\in Prime}^{p{r}_{i-1}}f(j)$ 给加回来， $\sum _{j\in Prime}^{p{r}_{i-1}}f(j)$ 即为 $g(p{r}_{i-1},i-1)$。

这样它们再乘一个 $p{r}_i$ ，则得到 $n$ 以内的最小质因子等于 $p{r}_i$ 的合数的 $f$ 值。注意这里，要求 $f$ 是一个完全积性函数，才能把 $f(p{r}_i)$ 提取出来。但是 $f$ 不一定是一个积性函数啊？带着疑问继续往下看。


注意这个递推式，它的初始条件是什么呢？是 $g[n][0]$ ，而 $g[n][0]$ 的意义正是还没有开始进行埃氏筛时的 $f$ 值之和。这个值是我们需要去求的，怎么可能拿来做初始值呢？

其实这里的 $g[n][0]$ 里，并不是真正的 $f$ 值之和，假设它为 $f^{\prime }$ 。在质数和质数的幂的位置，$f^{\prime }=f$；而其他位置不一定，$f^{\prime }$ 出现的目的，只是因为这里需要一个完全积性函数，而原来的 $f$ 虽然是一个积性函数，但不是完全积性函数。于是用 $f^{\prime }$ 去代替 $f$。这样，前面的递推式就成立了。

有时候题目中的 $f$ 是多项式，我们可以将它拆开，这样每一项都是一个幂的形式，而幂是完全积性函数。这样对每一项通过 $g$ 的递推式去求，求出后再求和即可。


怎么实现呢?

注意到第二维是可以滚动的，所以空间上可以省掉第二维；有因为 $\lfloor \frac{\lfloor \frac{n}{a}\rfloor }{b}\rfloor =\lfloor \frac{n}{ab}\rfloor$，这说明递归下去求的所有 $g$ 值，都在数论分块的 $2\sqrt{n}$ 个值中。所以我们一开始就把 $2\sqrt{n}$ 个值先存下来，然后在上面进行滚动。


现在进入正题，上面的都是预处理。

设 $S(n,i)$ 表示 $n$ 以内的最小质因子大于 $p{r}_i$ 的数的 $f$ 值之和。
则有 $$S(n,i)=g(n,|P|)-g(p{r}_i,|P|)+\sum _{j>i}\sum _{p{r}_j^k\le n}f(p{r}_j^k)\times (S(\lfloor \frac{n}{p{r}_j^k}\rfloor ,j+[k>1])$$

这里有同学提出过问题，为什么不能把 $g(n,|P|)-g(p{r}_i,|P|)$ 去掉，将 $[k>1]$ 改成 $[k\ge 1]$ 呢？
可以是可以的，但是就必须要把 $n$ 以内所有的质数都枚举出来
那 O(n) 的时间复杂度和直接暴力求前缀和有什么区别？

我们最终要求的值为 $S(n,0)+f(1)$。（加上 $f(1)$ 是因为1没有质因子，不会被 $S(n,0)$ 所包括）。

观察上述的递推式，其中的两项已经求出来了，最后的那一项有两个求和号，分别枚举质因子以及质因子的次数，注意此处根据“递归下去求的所有 $g$ 值，都在数论分块的 $2\sqrt{n}$ 个值中”，要求的质因子为 $\sqrt{n}$ 以内的质因子，所以枚举的总次数大约是：$\sqrt{\frac{n}{\ln n}}\times \ln n$，而 $S(\lfloor \frac{n}{p{r}_j^k}\rfloor )$中的参数，也是在 $n$ 的数论分块的 $O(\sqrt{n})$ 个值以内。

分析时间复杂度

设 $T(n)$ 表示上述递推式的时间复杂度，则有：
$$T(n)=O(\sqrt{\frac{n}{\ln n}}\times \ln n)+\sum _{p{r}_j^k}T(\lfloor \frac{n}{p{r}_j^k}\rfloor )$$

$$=O(\sqrt{\frac{n}{\ln n}}\times \ln n)+\frac{1}{\ln n}\sum _{i=2}^{n}T(\lfloor \frac{n}{i}\rfloor )$$

$$=O(\sqrt{\frac{n}{\ln n}}\times \ln n)+\frac{1}{\ln n}\sum _{i=2}^{n}O(\sqrt{\frac{\frac{n}{i}}{\ln (\frac{n}{i})}}\times \ln (\frac{n}{i}))$$

$$=O(\sqrt{\frac{n}{\ln n}}\times \ln n)+\frac{1}{\ln n}\sum _{i=2}^{\sqrt{n}}O(\sqrt{\frac{i}{\ln (i)}}\times \ln (i)+\sqrt{\frac{\frac{n}{i}}{\ln (\frac{n}{i})}}\times \ln (\frac{n}{i})$$

$$\ge O(\sqrt{\frac{n}{\ln n}}\times \ln n)+\frac{1}{\ln n}\sum _{i=2}^{\sqrt{n}}O(\sqrt[4]{n\ln \sqrt{n}})$$

$$=O(\sqrt{\frac{n}{\ln n}}\times \ln n)+O(\frac{n^{\frac{3}{4}}}{\ln n}\times \sqrt[4]{\ln \sqrt{n}})$$

$$=O(\frac{n^{\frac{3}{4}}}{\ln n})$$

例题

【模板】Min_25筛

简单的函数