该文章部分内容摘抄自 啊哈磊老师的《啊哈！算法》
一本对算法新手非常友好的书，非常推荐新手去阅读！

1.什么是深度优先搜索（DFS）

Deep First Search（简称DFS）
中文名也就是深度优先搜索

DFS其过程简要来说就是
对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.

DFS其实是属于图算法中的一种

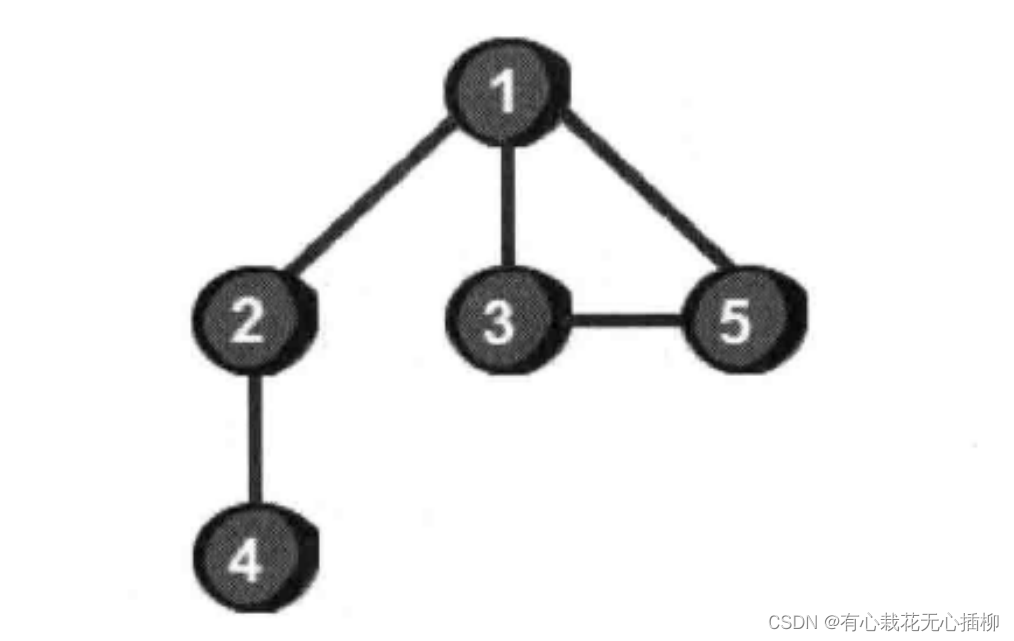
首先，这是一个 “图”，我们要把它的每个点都遍历一遍，
沿着一条路一直走，一直到不能走为止，这个过程可以被称为
“深度优先搜索”。

然后，我们的目的是把所有点都走一遍，
当1 -> 2 -> 4 走到无路可走时，退回到2
退回到2时，我们会发现，2处也无路可走，那么就退回到1
然后退回到1后，有路可以走了，走1 -> 3
3处有路可以走，走到5，
就是1 -> 3 -> 5

走的次序就是

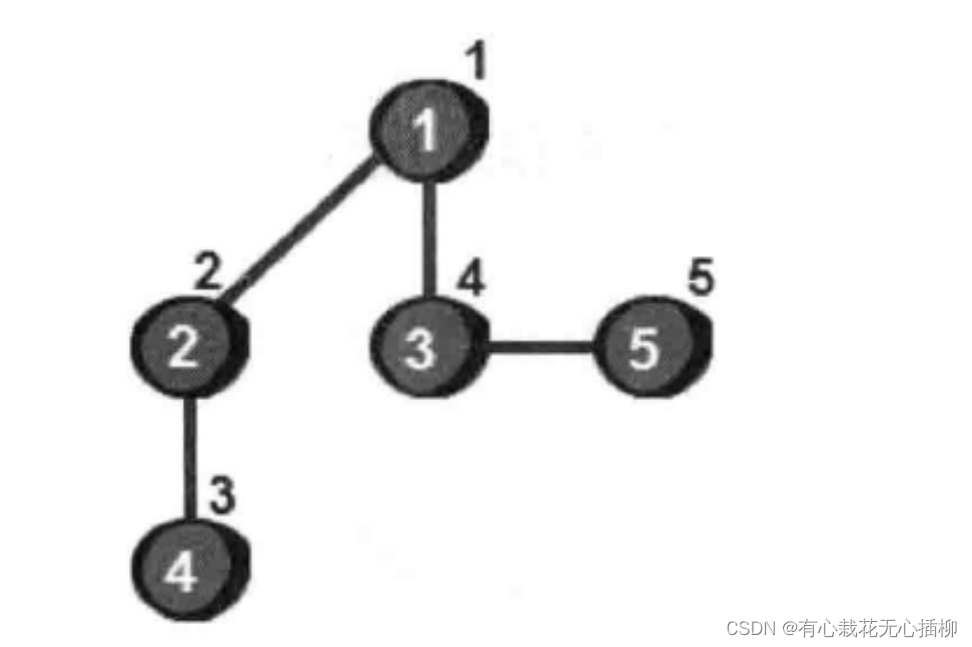
这就是DFS走的结果

深度优先搜索的思想就是

以一个未被访问的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；当没有为访问过的顶点时，则回到上一个顶点，继续试探访问别的顶点，直到所有的顶点都被访问过。
回到上一个顶点的过程也叫做 “回溯”
“回溯“也是非常重要的过程，我们需要恢复到原来的场景。

具体过程慢慢看下面的代码分析就能明白了。

2.结合例子看DFS

2.1 全排列数字

题目：

我们来看一下在这个经典的全排列数字的问题。
假如我们没有学过DFS，我们会怎么做？
先思考几分钟。再往下看

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

//你可能已经想出来了，就是这种暴力枚举的方法。
//其实我们的搜索法也是非常暴力的一种方法
//不过是在代码上做了一些优化。
int main()
{
	for(int a = 1;a <= 3 ;a++)
	{
	    for(int b = 1;b <= 3; b++)
	    {
	        for(int c = 1;c <= 3;c++)
	        {
	            if(a != b && a != c && b !=c )
	            {
	                printf("%d %d %d \n",a,b,c);
	            }
	        }
	    }
	}
}
/*1 2 3 
  1 3 2 
  2 1 3 
  2 3 1 
  3 1 2 
  3 2 1*/

下面，我们来看一下，用DFS这道题该怎么做

我们把这个问题形象一点给大家再次介绍。

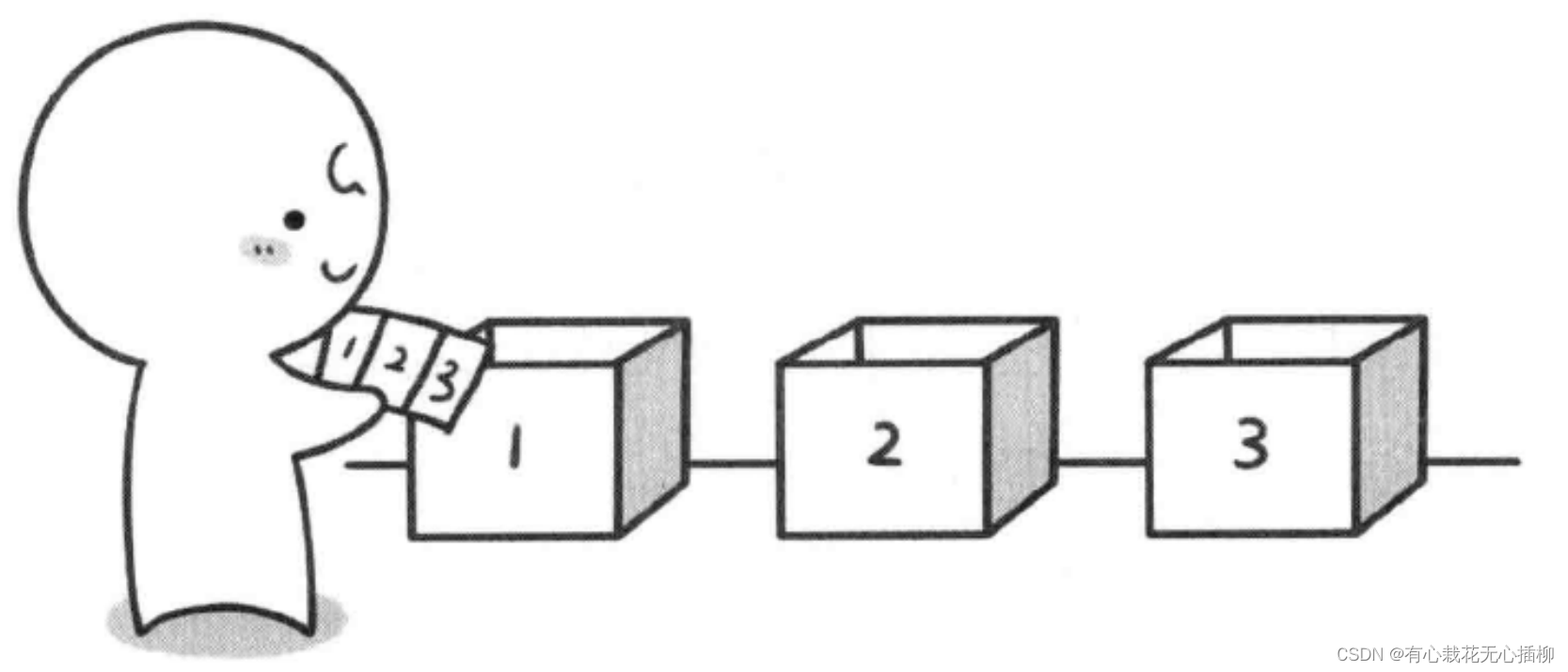
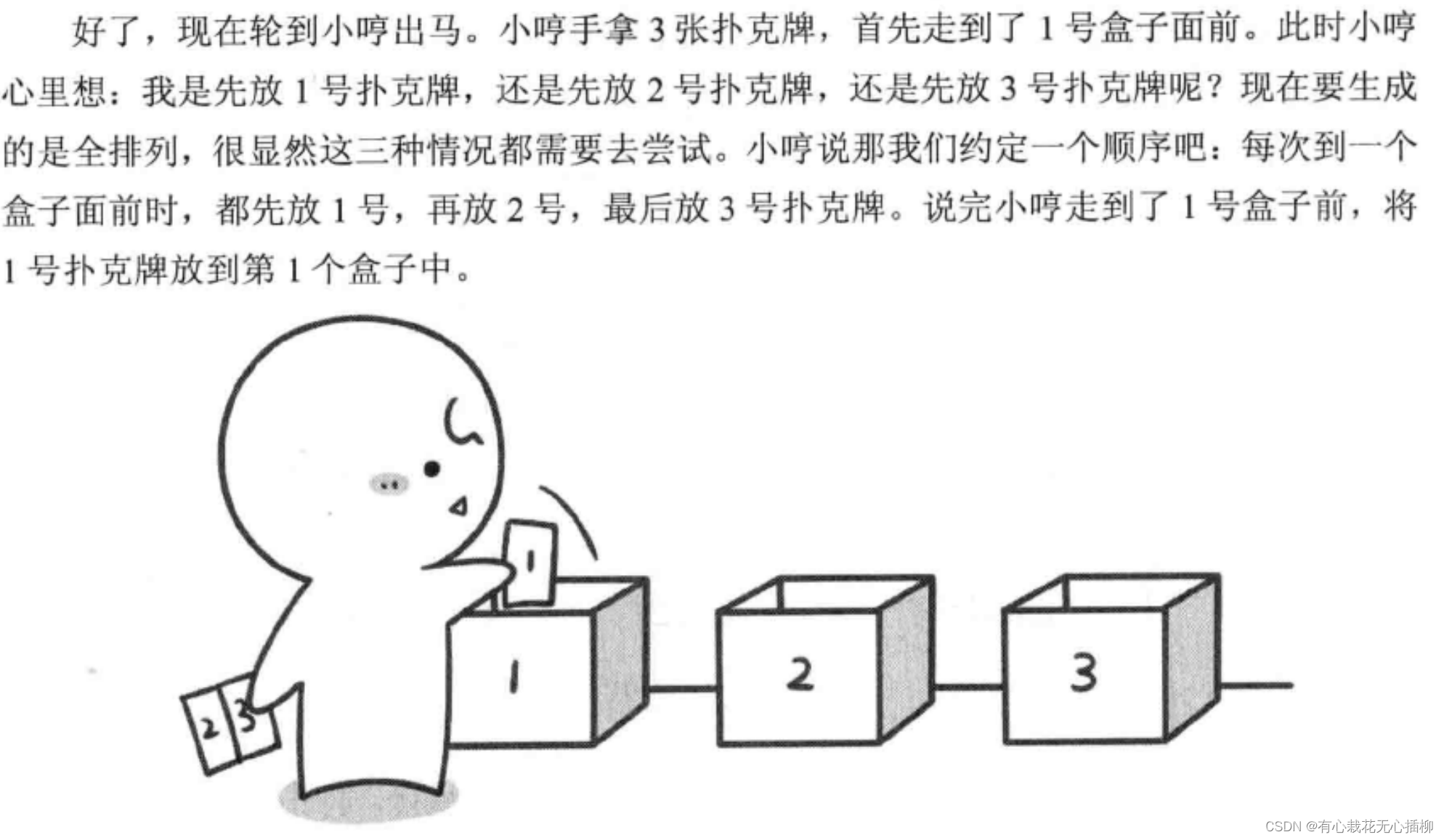
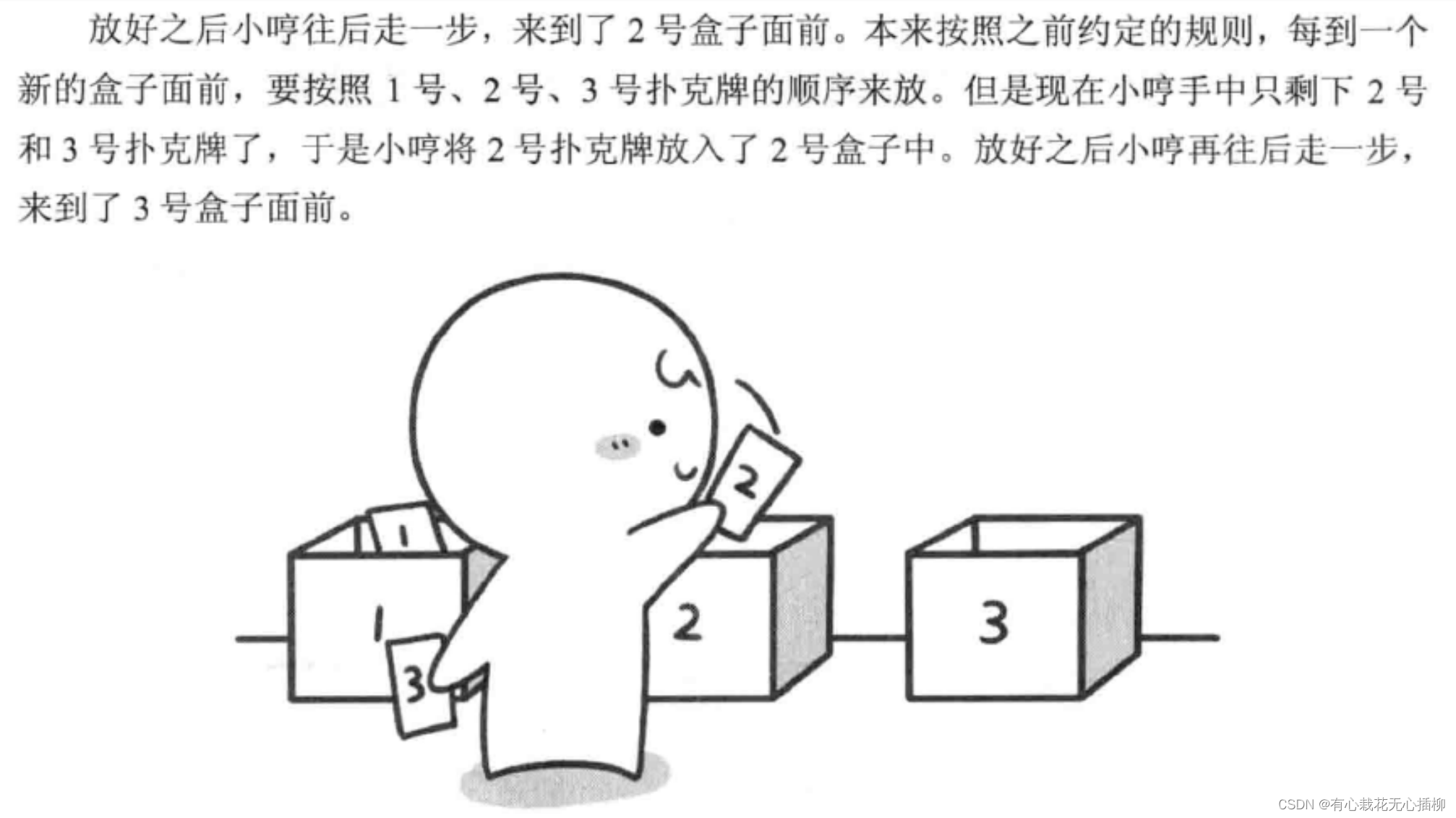
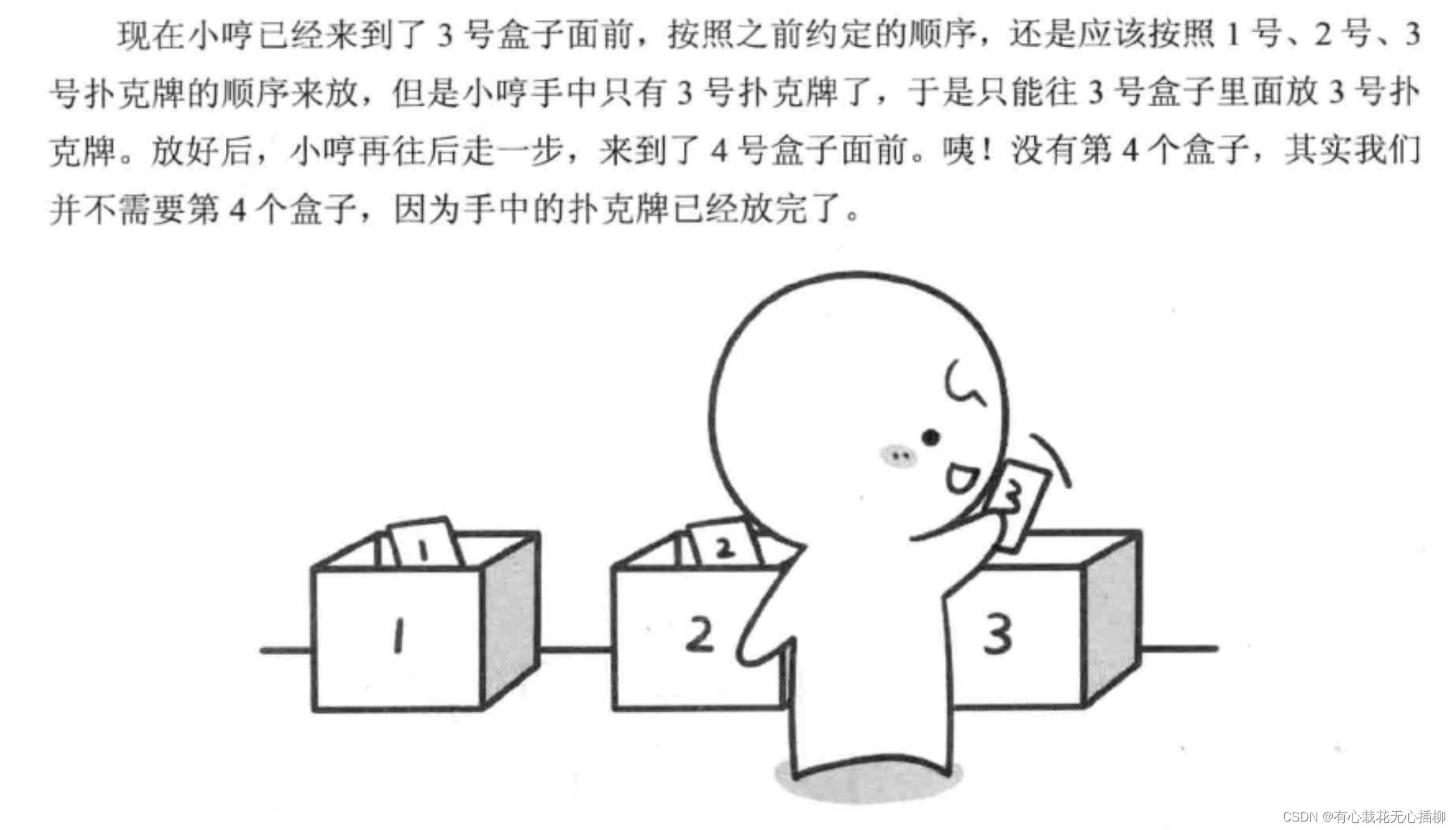
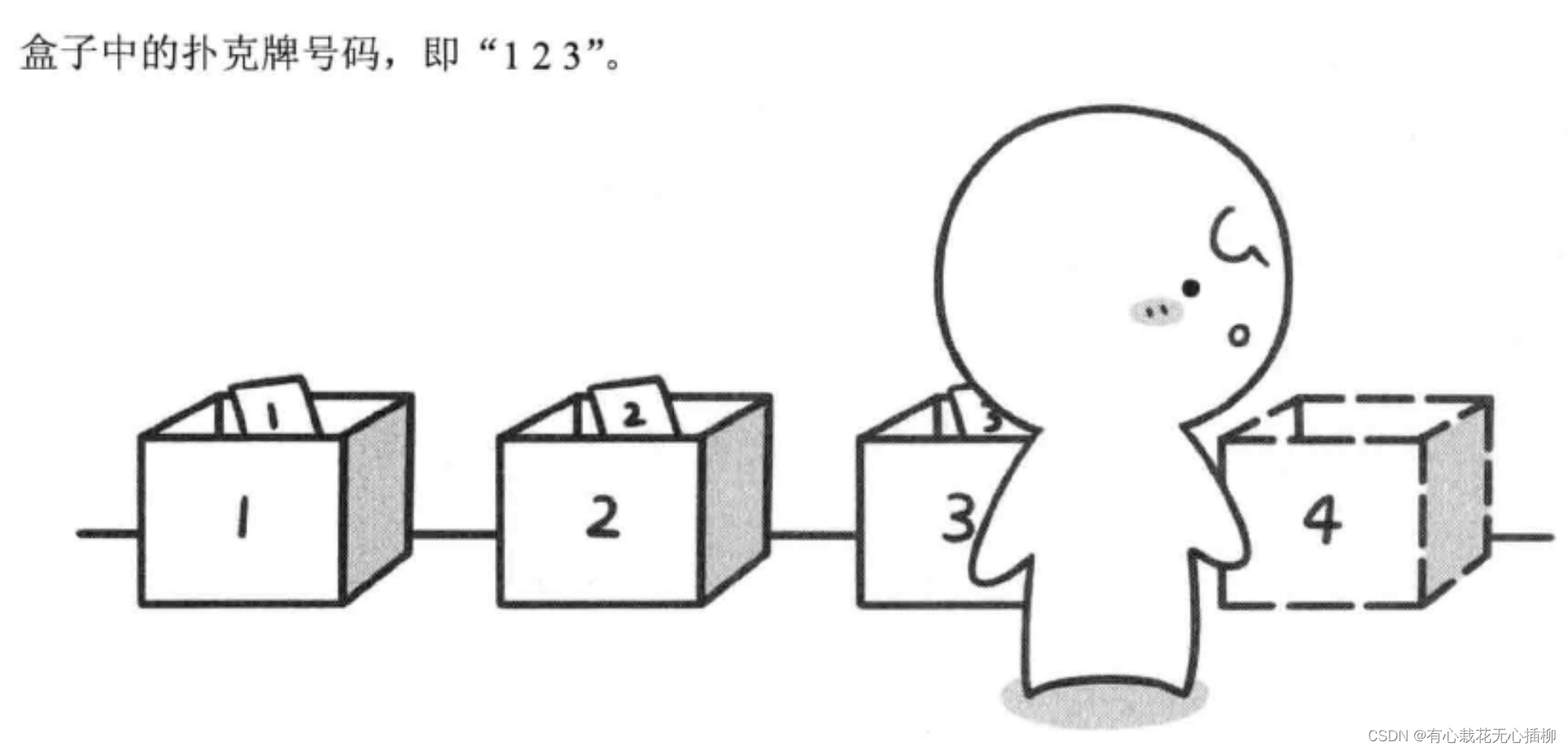
注：再次强调！以上文字内容摘抄自 啊哈磊老师的《啊哈！算法》
非常感谢有这么一位好的老师，能把复杂的算法给新手小白讲明白。

for(i = 1;i <= n;i++)
{
	a[step] = i;//将i号扑克牌放入到第step个盒子中
}

这里的数组a是用来表示小盒子的，变量step表示当前正处在第step个小盒子面前。a[step] = i;就是将第i号扑克牌，放入到第step个盒子中。
这里有一个问题就是，如果一张扑克牌已经放到别的小盒子中了，那么此时就不能再放入同样的扑克牌到别的盒子中了，因为此时手里已经没有扑克牌了。因此还需要一个数组book来标记哪些牌已经使用了。

for(i = 1;i <= n;i++)
{
	if(book[i] == false) //等于false，表示第i号牌没有被使用过 
	{
		a[step] = i;  //把i号牌放入到第step个盒子中
		book[i] = true;  //把book[i] 设为true,表示已经用过了i号牌
	}
}

我们现在已经处理完第step个小盒子了，接下来需要往下走一步，去处理第step+1个小盒子。
如何处理呢？
处理方法其实和我们刚刚处理第step个小盒子的方法相同。
把它封装成一个函数

void dfs(int step) // 表示站在第step个小盒子面前
{
	for(int i = 1; i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌是否用过
		{
			a[step] = i; //没用过就把第i号扑克牌放入第step个小盒子
			book[i] = true;//book[i]设为true，表示第i号扑克牌我们已经用过
		}
	}
}

把这个过程变成函数以后，就好处理第step + 1 个盒子了
就是 dfs(step + 1),来看代码

void dfs(int step) // 表示站在第step个小盒子面前
{
	for(int i = 1; i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌是否用过
		{
			a[step] = i; //没用过就把第i号扑克牌放入第step个小盒子
			book[i] = true;//book[i]设为true，表示第i号扑克牌我们已经用过


			dfs(step + 1);//通过函数递归来实现（函数自己调用自己）
			book[i] = false;
//这里是非常重要的一步，一定要将刚才尝试的扑克牌收回，才能进行下一次尝试
		}
	}
}

book[i] = false;
这一步非常重要，也就是我们上面说的回溯，回溯要恢复到原来的场景。
也就是我们把扑克牌收回，否则无法进行下一次的摆放。

现在还有一个问题，就是什么时候输出一个满足要求的序列呢？
其实当我们处理第n + 1个小盒子的时候（即step = n + 1），说明前n个小盒子已经放好扑克牌了，这里将1~n个小盒子中的扑克牌编号打印出来就可以了。注意！打印完毕之后一定要return，否则程序就会永无止境地进行下去了，也就是要有递归的终止条件。

void dfs(int step) // step 表示现在站在第几个盒子面前
{
	if(step == n + 1) //如果站在第n+1个盒子面前，则表示前n个盒子已经放好扑克牌
	{
	//输出一种排列，即 1 ~ n 号盒子中扑克牌编号
		for(int i = 1;i <= n;i++)
		{
			printf("%d ",a[i]);
		}
		printf("\n");
		return; // 返回之前的一步（最近一次调用dfs的地方）
	}
	for(int i = 1;i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌i是否已经用过
		{
			a[step] = i; //如果没用过，就把i号牌放在第step个盒子
			book[i] = true;//i号牌记录为已经用过
			dfs(step + 1);//处理第step+1个盒子，函数递归实现
			book[i] = false;//将刚才的扑克牌收回，才能进行下一次尝试
		}
	}
}

完整代码如下

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 10;
int n;
int a[N];//开辟的盒子
bool book[N]; //这里是全局变量，默认为false
void dfs(int step) // step 表示现在站在第几个盒子面前
{
	if(step == n + 1) //如果站在第n+1个盒子面前，则表示前n个盒子已经放好扑克牌
	{
	//输出一种排列，即 1 ~ n 号盒子中扑克牌编号
		for(int i = 1;i <= n;i++)
		{
			printf("%d ",a[i]);
		}
		printf("\n");
		return; // 返回之前的一步（最近一次调用dfs的地方）
	}
	for(int i = 1;i <= n;i++)
	{
		if(book[i] == false) // 判断扑克牌i是否已经用过
		{
			a[step] = i; //如果没用过，就把i号牌放在第step个盒子
			book[i] = true;//i号牌记录为已经用过
			dfs(step + 1);//处理第step+1个盒子，函数递归实现
			book[i] = false;//将刚才的扑克牌收回，才能进行下一次尝试
		}
	}
}
int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

这段简单的例子，核心的代码不超过20行
但是却饱含了DFS的基本模型
理解深度优先搜索关键在于解决“当下该如何做”。
至于“下一步该如何做”则与“当下该如何做是一样的”
比如我们这里写的dfs(step)函数的主要功能就是解决当你在第step个盒子的时候你该怎么办。通常的方法就是把每一种可能都去尝试一遍（一般使用for循环来遍历）。当前这一步解决后便进入下一步dfs（step + 1）。下一步的解决方法和当前这步的解决方法是完全一样的。下面的代码就是深度优先搜索的基本模型

```c
void dfs(int step)
{
	判断边界
	尝试每一种可能for(i = 1;i <= n;i++)
	{
		继续下一步 dfs(step+1);
	}
	返回
}

每一种尝试就是一种“扩展”。每次站在一个盒子面前的时候，其实都有n种扩展方法，但是并不是每种扩展方法都能扩展成功的。

结语

再次感谢啊哈磊老师，能把这些复杂的算法思想讲得如此透彻，为刚接触算法新手小白留了一条路，非常感谢！