机器学习理论基础—聚类算法

聚类的距离计算

聚类：物以类聚。将相似的样本聚集到一起，使得同一类簇的样本尽可能接近,不同类簇的样本尽可能远离。（无监督算法）

对于距离的定义：满足下面的四个特点

1. 非负性
2. 同一性
3. 对称性
4. 传递性

常用的距离度量（连续/离散有序）

• 明可夫斯基距离(Minkowski distance)
  
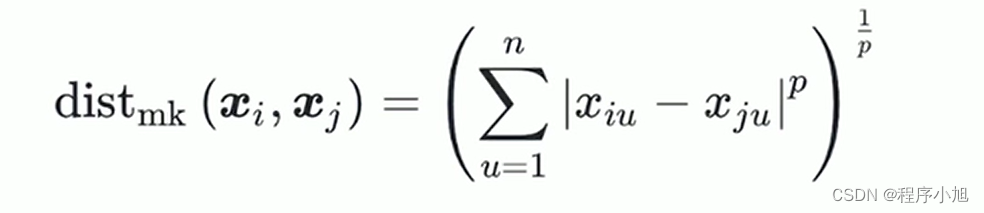
• 当p=2时退化为欧式距离(Euclidean distance)
  
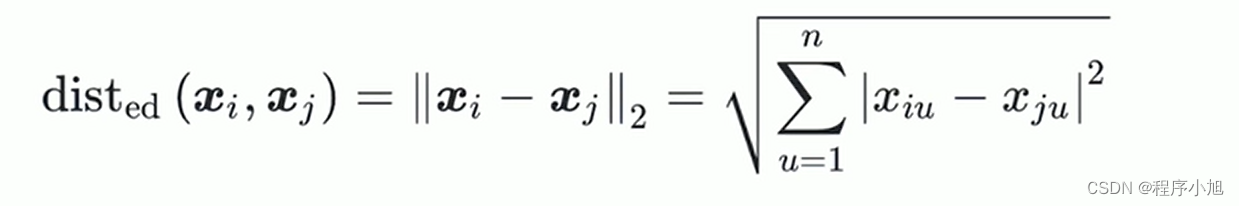
• p = 1 退化成曼哈顿距离(Manhattan distance)只能沿着坐标轴的方向来进行计算
  

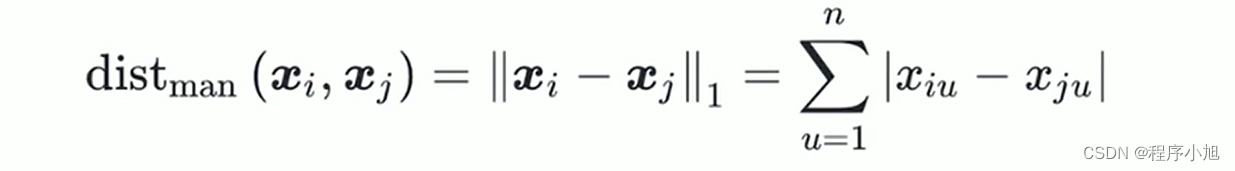
常用的距离度量（离散无序）

使用VDM (Value Difference Metric)方法来进行度量。

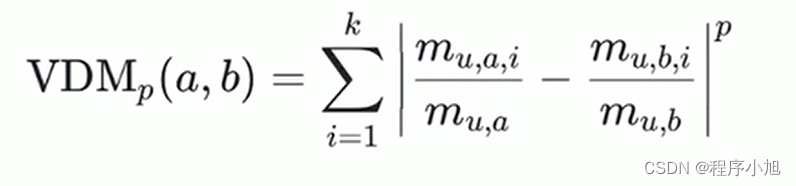
m:特征u取值a的情况下的数量

原型聚类

常用的原型聚类算法是kmeans算法

原型(prototye)指类结构能通过一组典型的特例刻画。比如男、女类似的。给定样本集D={x1,x2，···，xm}，k均值算法针对聚类所得簇划分C={C1，C2，···，Ck}，求解最小化平方误差问题

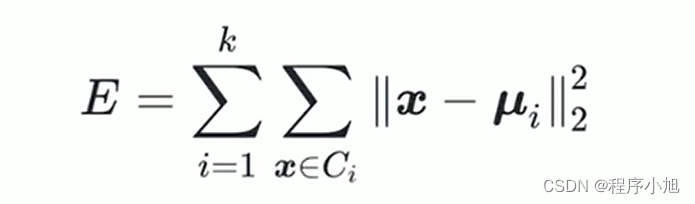
求解改式需要考虑样本集D所有可能的划分，是一个NP-hard问题。一般来说，我们采用迭代算法求解近似划分。

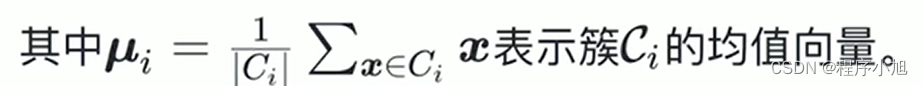
kmeans算法的流程

密度聚类

常用的密度聚类算法为：DBSCAN

密度聚类假设聚类结构能够通过样本分布的紧密程度确定。它从样本密度的角度考察样本间的可连接性，并基于可连接样本不断扩展聚类簇得到最终的聚类结果。DBSCAN是密度聚类的代表之一。 它基于一组邻域参数(∈,MinPts)刻画样本分布的紧 密程度。关于DBSCAN的几个概念如下：

DBSCAN定义的簇为：最大密度相连的样本集合为一个簇。

1. 连接性：同一个簇内任意两样本必然密度相连
2. 最大性：密度可达的两个样本必定属于同一个簇

算法的流程步骤：

层次聚类

层次聚类试图将数据划分成为不同的层次，因此聚类结果呈现明显的树状结构。

AGNES是一种采用自底向上聚合策略的层次聚类算法。在聚类过程中不断合并距离最近的两个类簇，知道达到预期的聚类簇数目。算法的核心在于如何定义类簇中之间的距离

• 最小距离（两个簇最近的样本距离）
  

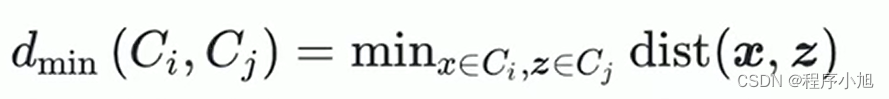
• 最大距离（两个簇最远的样本距离）
  

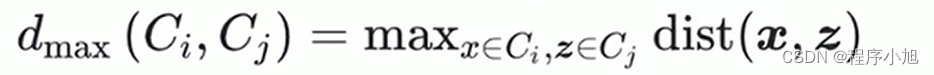
• 平均距离（两个簇两两平均的样本距离）
  
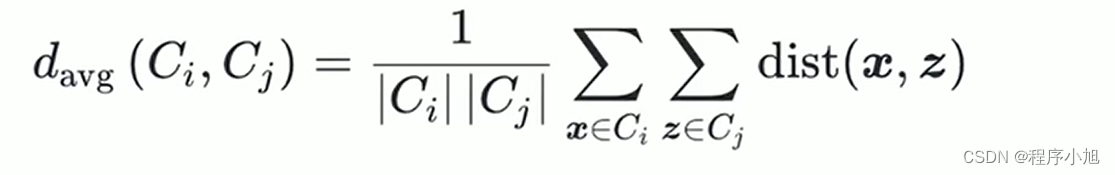
  AGNES算法流程
  

总结：结合西瓜书中的具体案例来进行进一步的学习，文章只是对聚类算法进行简单的概述