一、说明

   上文中叙述母体和抽样的设计；以及抽样分布的概念，本篇将这种关系定量化，专门针对抽样的指标参数和母体参数的对应关系，这是我们以后做检验的基础。

二、抽样分布

   考虑从给定的母体中抽取容量为N的所有可能样本（抽样时无论放回和不放回）。对于每一个样本，我们可以计算出某个统计量（如均值、标准差）的值，不同样本得到的统计量（均值或标准差）不同，用这种方法得到的统计量分布称为抽样分布。
抽样分布有多种，我们这里重点介绍几个典型抽样分布.

•    均值抽样分布。
•    比例抽样分布。
•    和（差）抽样分布。

三 均值抽样分布

   均值抽样是最常见的抽样。我们知道抽样的目的是从若干个局部，推演出全局的过程。推而广之，从个别是不是属于一个全局的概率。这其实有一个先验前提，母体基本情况是确定的。因此，预先知道母体的基本信息有：

•    有限母体
•    无限母体
  从抽样方式上，又分为：
•    无放回抽样
•    有放回抽样
  下面我们将分别叙述。

3.1 有限母体无放回抽样

   假定一个有限母体，容量为$N_p$.母体均值和方差为：$\mu ,\sigma$。抽样的容量为N，均值方差记号为${\mu }_{\bar{x}},{\sigma }_{\bar{x}}$,那么，抽样的均值和方差与母体的均值和方差存在下列关系：

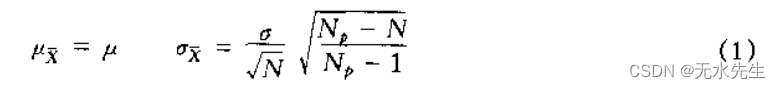
   以上关系我们给出一个实例说明：
   给出一个母体 { 2 , 3 , 6 , 8 , 11 } \{2,3,6,8,11\} {2,3,6,8,11},从母体中有放回地抽样，抽样的容量是2；

   如何获取母体的均值和方差？
$$\begin{gathered} \mu =\frac{2+3+6+8+11}{5}=6 \\ {\sigma }^2=\frac{(2-6{)}^2+(3-6{)}^2+(6-6{)}^2+(8-6{)}^2+(11-6{)}^2}{5}=10.8 \end{gathered}$$
$$\sigma =3.29$$
   如何获取抽样的均值和方差？
   从总体中抽取容量为2的样本，而且是无放回的，这说明什么？

•    当抽出一个数以后，不放回再抽取第二个，说明两个数不能一样。
•    当抽取出（a，b）和（b，a）属于同一个抽样。
  这样的抽样共有$C_5^2$种，分别是：

Column 1	Column 2	均值
2	3	2.5
2.	6	4
2	8	5
2	11	6.5
3.	6	4.5
3	8	5.5
3	11	7
6	8	7
6	11	8.5
8	11	9.5

样本均值为：
${\mu }_{\bar{x}}=\frac{2.5+4+5+6.5+4.5+5.5+7+7+8.5+9.5}{10}=6$
样本方差：


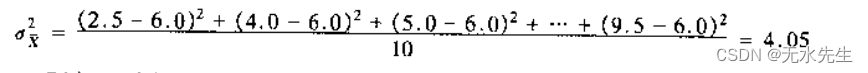
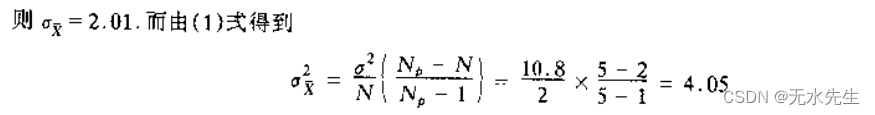
   因此，符合我们给出的（1）式。

3.2 有限母体有放回抽样

   有限母体和抽样中，母体均值和抽样的关系。
${\mu }_{\bar{x}}=\mu {\sigma }_{\bar{x}}=\frac{\sigma }{\sqrt{N}}$ (2)

3.3 无限母体

   对于无限的母体，它和有限母体的有放回抽样是一样的，
无限的母体的抽样中，母体均值和抽样的关系。
${\mu }_{\bar{x}}=\mu {\sigma }_{\bar{x}}=\frac{\sigma }{\sqrt{N}}$ (3)

   好了，我们以上对均值的抽样做出完整解释。下面请看比例抽样是个什么概念。

四、比例抽样分布

   关键词： sampling distribution of proportions
   有一类事物，总是能归结到某事物发生或不发生的概率。这是一个二分法问题，比如，进入某商店的客人中，购买商品的顾客比例。这种问题可以归结到抛硬币问题，或者二项式分布问题。
   总体设定：将总体看成是0-1分布，均值和方差为：
$\mu =p;{\sigma }^2=p(1-p)$
   那么，抽样的均值和方差分别是：
${\mu }_p=p;{\sigma }_p=\sqrt{\frac{p(1-p)}{N}}$ (3)
   这个结论和有限，有放回抽样的结果一样的。

五、和差抽样分布

和差抽样分布，是针对；对两个母体分别抽样，然后估算两组抽样中指标数（如均值）和、差的统计运算。因为正寻找最合适的实例，暂时停止，做个记号，日后完善。
（在下文叙述}