目录
BFS
BFS:找最短路路径
BFS:用队列实现
特点
最短路径问题用BFS
应用场合
例题一
【思路】
输出路径的两种方法
简单方法
标准方法(栈)
BFS:连通性判断
例题二:全球变暖
【思路】
BFS的三种实现
1、queue实现
2、 list实现
3、deque (推荐)
例题三:剪邮票
【思路】
【代码演示】
BFS
- BFS搜索原理:“逐层扩散”。从起点出发,按层次从近到远,逐层先后搜索。
- 编码:用队列实现
- 应用:BFS一般用于求最短路径问题,BFS的特点是逐层搜索,先搜到的层离起点更近。
BFS:找最短路路径
找从@到*的最短路径

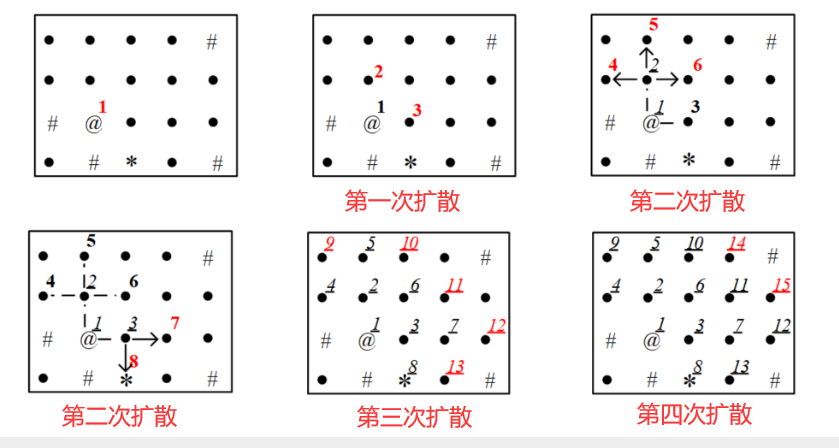
BFS:用队列实现
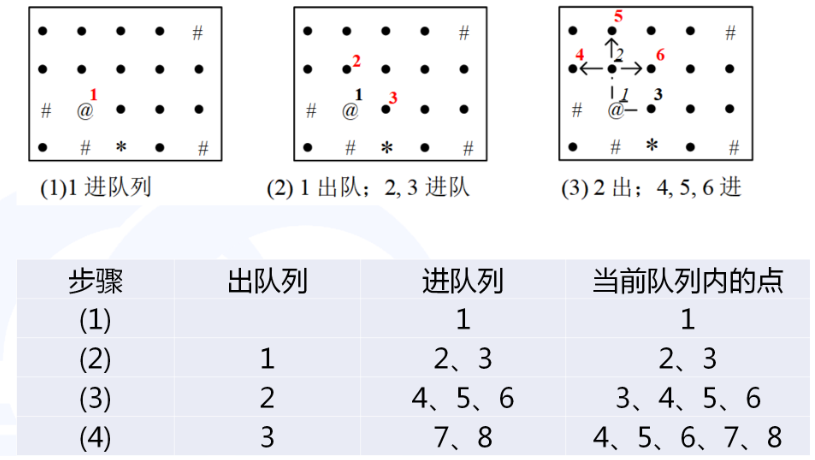
特点:
- 队列中最多只能存在两层的点。例如在第二层的点没有出队之前,第三层不会扩散出第四层。
- 每次离开队列的队头,已经找到了从起点到该点的最短路径。
最短路径问题用BFS
BFS的特点:逐层扩散。
- 往BFS的队列中加入邻居结点时,按距离起点远近的顺序加入:先加入距离起点为1的邻居结点,加完之后,再加入距离为2的邻居结点,等等
- 搜完一层,才会继续搜下一层。
最短路径:从起点开始,沿着每一层逐步往外走,每多一层,路径长度就增加1 。
所有长度相同的最短路径都是从相同的层次扩散出去的。
搜到第一个到达终点的路径,就是最短路径。
应用场合:
点和点直连的距离是1(边长是1),即两点之间距离都是相等的。例如方格图。
例题一
迷宫2019年第十届省赛,填空题,lanqiao0.J题号602
【题目描述】
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
下图给出了一个迷宫的平面图,其中标记为 1 的为障碍,标记为 0 的为可以通行的地方。
010000 000100 001001 110000迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这 个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按
DRRURRDDDR的顺序通过迷宫, 一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫(30 行 50 列),请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。请注意在字典序中 D<L<R<U。
01010101001011001001010110010110100100001000101010 00001000100000101010010000100000001001100110100101 01111011010010001000001101001011100011000000010000 01000000001010100011010000101000001010101011001011 00011111000000101000010010100010100000101100000000 11001000110101000010101100011010011010101011110111 00011011010101001001001010000001000101001110000000 10100000101000100110101010111110011000010000111010 00111000001010100001100010000001000101001100001001 11000110100001110010001001010101010101010001101000 00010000100100000101001010101110100010101010000101 11100100101001001000010000010101010100100100010100 00000010000000101011001111010001100000101010100011 10101010011100001000011000010110011110110100001000 10101010100001101010100101000010100000111011101001 10000000101100010000101100101101001011100000000100 10101001000000010100100001000100000100011110101001 00101001010101101001010100011010101101110000110101 11001010000100001100000010100101000001000111000010 00001000110000110101101000000100101001001000011101 10100101000101000000001110110010110101101010100001 00101000010000110101010000100010001001000100010101 10100001000110010001000010101001010101011111010010 00000100101000000110010100101001000001000000000010 11010000001001110111001001000011101001011011101000 00000110100010001000100000001000011101000000110011 10101000101000100010001111100010101001010000001000 10000010100101001010110000000100101010001011101000 00111100001000010000000110111000000001000000001011 10000001100111010111010001000110111010101101111000
【思路】
题目求字典序最小的最短路径
在每次扩散下一层(往BFS的队列中加入下一层的结点)时,按字典序“D<L<R<U”的顺序加下一层的结点,那么第一个搜到的最短路径就是字典序最小的。
计算复杂度:每个点只搜一次,即进入队列和出队列一次。复杂度O(n),n是迷宫内结点的总数。
BFS能用于解决1千万个点的最短路问题。
输出路径的两种方法
简单方法
- 每扩展到一个点v,都在v上存储从起点s到v的完整路径。扩展到下一个点u时,只需要将从起点s到v的完整路径加入v到u的路径即可。到达终点t时,得到了从起点s到t的完整路径。
- 优点:简单、适合小图。
- 缺点:占用大量空间,因为每个点上都存储了完整的路径。不适合大图。
from queue import Queue
import sys
mp = []
for i in range (0,30):mp. append (input()) # 读迷宫
# 加上围墙,就不需要再判断出界问题
for i in range (len(mp) ) :
mp[i] = '1'+ mp[i] + '1' # 为迷宫加左边和右边的围墙
mp = [52 * '1'] + mp +[52* '1'] # 为迷宫加上面和下面的围墙
vis = [list(map(int,list(i))) for i in mp] # 记录迷宫的状态
k = ('D', 'L', 'R', 'U') # 四个方向
dir = ((1,0),(0,-1),(0,1),(-1,0))
# BFS:队列实现
vis[1][1] = 1 # 起点是(1,1),终点是(30,50)
q= Queue() # 队列:坐标x、坐标y、路径
q. put ((1,1,"")) # 以(1,1)为起点开始移动
while q.qsize() != 0: # 若队列不为空
x,y,p = q.get () # 弹出队头
if x==30 and y==50:print(p) ; sys.exit() # 终止条件:到达右下角。打印完整路径,退出
for i in range(4) : # 遍历邻居点的四个方向
nx = x + dir[i][0]
ny = y + dir[i][1]
if vis[nx][ny] != 1: # 把访问过的点变成墙,后面不再访问
vis[nx][ny] = 1
path = p+k[i] # path:记录从起点到这个点的完整路径
q.put ((nx,ny,path)) # 加入队头的邻居点标准方法(栈)
- 在每个点上记录它的前驱点
- 从终点一步步回溯到起点,得到一条完整路径。
优点::节省空间,因为每个点上只存储了上一个点。适合大图。
(在DFS中,路径可以用栈来记录,参考19讲例题“路径之谜,lanqiaoOJ题号89”)
from queue import Queue
import sys
# 打印路径:从终点递归到起点,然后打印
def print_path(x, y):
if x==1 and y==1: return # 回溯到了起点,递归结束,返回
if pre[x][y]=='D': print_path(x-1, y) # 回溯,往上U
if pre[x][y]=='L': print_path(x, y+1) # 回溯,往右R
if pre[x][y]=='R': print_path(x, y-1)
if pre[x][y]=='U': print_path(x+1, y)
print(pre[x][y], end="") # 最后回溯到(1,1)开始打印
mp = []
for i in range (0,30):mp. append (input()) # 读迷宫
# 加上围墙,就不需要再判断出界问题
for i in range(len(mp)):
mp[i] = '1'+ mp[i] + '1' # 为迷宫加左边和右边的围墙
mp = [52 * '1'] + mp +[52* '1'] # 为迷宫加上面和下面的围墙
vis = [list(map(int,list(i))) for i in mp] # 记录迷宫的状态
# 坐标x:向下递增;坐标y:向右递增
k = ('D', 'L', 'R', 'U') # 四个方向:按字典序从小到大来排,先访问字典序小的
dir = ((1,0),(0,-1),(0,1),(-1,0))
pre = [[(-1,-1)] * 52 for i in range(32)] # 用于保存前一个点
# BFS:实现队列
vis[1][1] = 1 # 起点是(1,1)
q = Queue()
q.put ((1,1)) # # 以(1,1)为起点开始移动
while q.qsize() != 0: # 队列不为空
x, y = q.get () # 弹出队头
if x==30 and y==50: print_path(30,50);sys.exit() # 终止条件:到达右下角。打印完整路径,退出
for i in range(4): # 遍历邻居点的四个方向
nx = x + dir[i][0]
ny = y + dir[i][1]
if vis[nx][ny] != 1: # 把访问过的点变成墙,后面不再访问
vis[nx][ny] = 1
pre[nx][ny] = k[i] # pre:记录它的前驱点
q.put((nx,ny)) # 加入队头的邻居点BFS:连通性判断
连通性判断:
图论的一个简单问题,给定一张图,图由点和连接点的边组成,要求找到图中互相连通的部分。
在之前算法第八期中,用DFS讲解了连通性判断。
例题二:全球变暖
2018年第九届蓝桥杯省赛 lanqiao0J题号178
【题目描述】
你有一张某海域 NxN 像素的照片,"."表示海洋、"#"表示陆地,如下所示:. . . . . . .
. ##. . . .
. ##. . . .
. . . . ##.
. . ####.
. . . ###.
. . . . . . .
其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . #. .
. . . . . . .
. . . . . . .
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
【输入描述】
第一行包含一个整数 N (1≤N≤1000)。以下 N 行 N 列代表一张海域照片。
照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。、
【输出描述】
一个整数表示答案。
【输入输出样例】
输入7 ....... .##.... .##.... ....##. ..####. ...###. .......输出
1
【思路】
BFS判断连通性的步骤:
- 从图上任意一个点u开始遍历,把它放进队列中。
- 弹出队首u,标记u已搜过,然后搜索u的邻居点,即与u连通的点,放到队列中。
- 继续弹出队首,标记搜过,然后搜索与它连通的邻居点,放进队列。
继续以上步骤,直到队列为空,此时一个连通块已经找到。
其他没有访问到的点,属于另外的连通块,按以上步骤再次处理这些点。最后所有点都搜到,所有连通块也都找到。
什么岛屿不会被完全淹没?
若岛中有个陆地,它周围都是陆地,那么这个岛 (称为高地)不会被完全淹没。
先用BFS搜出所有的岛 (连通块),再检查这个岛有没有高地,统计那些没有高地的岛 (连通块)的数量,就是答案。
计算复杂度:每个像素点只用搜一次且必须至少搜一次,共个点,DFS的复杂度是O(N^2),题目数据规模为1000,1000^2=10^6,可以满足要求。
注意:这一题不需要判断是否出界,因为题目规定最外围都是水,遇到水就停下来,不会出现越界的情况。
BFS的三种实现
可以用queue、list、deque来实现。其中deque最快。
用“全球变暖”这题演示三种实现。
1、queue实现
from queue import*
def bfs(x, y):
global flag
q= Queue ()
q. put ((x, y)) # 放入队列
vis[x][y]=1
while not q.empty ():# 队列不为空
x, y = q.get() # 弹出队头
if mp[x][y+1]=='#'and mp[x][y-1]=='#'and \
mp[x+1][y]=='#'and mp[x-1][y]=='#':# 判断上下左右是不是陆地(是不是高低)
flag = 1 # 高地
for i in range(4):#扩展4个方向
nx = x+dir[i][0];ny = y+dir[i][0]
if vis[nx][ny]==0 and mp[nx][ny]=="#":# 只搜索没有访问过且是陆地的点
q.put((nx, ny))
vis[nx][ny]=1
n = int (input ()) # n行n列
mp =[]
for i in range(n): mp. append(list(input() ))
vis = []
for i in range(n):vis.append ([0]*n)
dir =[(0,1),(0,-1),(1,0),(-1,0)]
ans = 0
# 对每个点进行搜索
for i in range(n):
for j in range(n):
if vis[i][j]==0 and mp[i][j]=="#": # 只搜索没有访问过且是陆地的点
flag = 0
bfs(i,j)
if flag == 0: ans+=1 # 不是高地,岛被淹没,ans加一
print(ans)2、 list实现
# 与其他方法不同的地方已用注释标出
def bfs (x, y):
global flag
q = [(x, y)] # 用list实现队列
vis[x][y]=1
while q: # 列表不为空
x, y = q. pop(0) # 弹出队头
if mp[x][y+1]=='#'and mp[x][y-1]=='#'and \
mp[x+1][y]=='#'and mp[x-1][y]=='#':flag = 1
for i in range(4):
nx = x+dir[i][0];ny = y+dir[i][0]
if vis[nx][ny]==0 and mp[nx][ny]=="#":
q. append((nx, ny)) # 加入队尾
vis[nx][ny]=13、deque (推荐)
deque最快:建议需要用队列时,用deque
# 与其他方法不同的地方已用注释标出
from collections import * # 导入库:collections
def bfs(x, y):
global flag
q = deque() # 用deque实现队列
q. append((x, y)) # 加入起始点
vis[x][y] = 1
while q: # 列表不为空
x, y = q.popleft() # 弹出队头
if mp[x][y+1]=='#'and mp[x][y-1]=='#'and \
mp[x+1][y]=='#'and mp[x-1][y]=='#':flag = 1
for i in range(4):
nx = x+dir[i][0];ny = y+dir[i][0]
if vis[nx][ny]==0 and mp[nx] [ny]=="#":
q. append((nx,ny)) # 加入队尾
vis[nx][ny]=1例题三:剪邮票
剪邮票2016年第七届蓝桥杯省赛,填空题,lanqiao0J题号1505
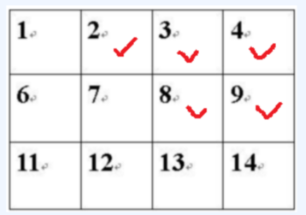
如图1, 有12张连在一起的12生肖的邮票。
现在你要从中剪下 5 张来,要求必须是连着的。
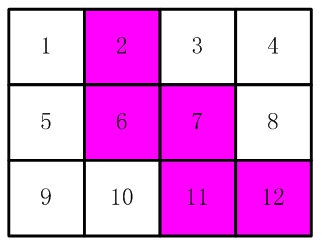
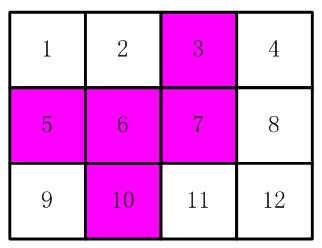
(仅仅连接一个角不算相连) 比如,图2和图3中,粉红色所示部分就是合格的剪取。
请你计算,一共有多少种不同的剪取方法。
【思路】
暴力求全排列+检查连通性。
(1)用递归暴力列出所有可能的排列:从12个数中选5个数进行全排列。
(2)判断这5个数是否连通。
算法复杂度:=12*11*10*9*8=12!/7!=95040可行!
判断2个数是否连通Z:
- 在原图中向上为-4,向下为+4,向左为-1,向右为+1,但是遇到34578这种4+1=5,这种情况不符合。
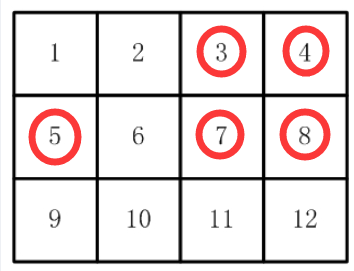
- 所以重构一下原图:改成向上为-5,向下为+5,向左为-1,向右为+1。
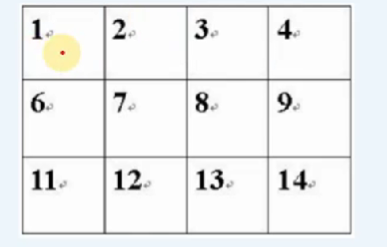
举例:判断图中的{2,3,4,8,9}是否连通。用队列:·
- 2进队列:当前队列是(2)
- 2的邻居进(push)队列:当前队列是(23)
- 弹出(pop)2:当前队列是(3);
- 3的邻居进队列:当前队列是(3 4 8)
- 弹出3;当前队列是(4 8)
- 4的邻居进队列:当前队列是(4 8 9)
- 弹出4:当前队列是(8 9)
- 8没有没处理过的邻居了
- 弹出8:当前队列是(9)
- 弹出9
- 队列空。
如果5个数都进过队列,它们就是连通的。
【代码演示】
from queue import *
def bfs (): # a[0]~a[4]这前5个数是递归出来的5个数。用BFS判断它们是否连
vis=[0]*5 # 这5个数的状态,判断其中某个数是否已经用队列处理过
p = 0 # 进队列的个数。如果5个数都进过队列,说明这5个数是连通的
q= Queue()
q.put(0) # 第一个进队列的数
vis[0]= 1 # 表示0用队列处理过了
# 将第i个数所有满足要求的邻居点放入队列
while not q. empty () :
i =q.get() # 得到队列的第一个数
p += 1 # 进队列数+1
for j in range (5):
if vis[j]==0: # j没有用队列处理过。
for k in (-1,1,-5,5) : # 遍历上下左右4个方向
if a[i]+k==a[j]: # 与j在k方向连接
q. put(j) # 进队列
vis[j]=1
if p==5: return True # 如果5个数都进过队列,说明这5个数是连通的
else: return False
def perm(s,t): # 套模板:在n个数里选m个数的排列数
global num
if s == 5:
if bfs() ==True: num+= 1 # 得到一个5个数的排列,用bfs判断5个数是否连
else:
for i in range(s,t+1):
a[s],a[i] = a[i],a[s] # 交换
perm(s+1,t)
a[i], a[s] = a[s],a[i]
a = [1,2,3,4,6,7,8,9,11,12,13,14] # 不包括5,10
num = 0 # 统计排列数
perm(0,11) # 求从第0个数到第11个数的全排列
print(num // 120) # 排列数除以5!=120得组合数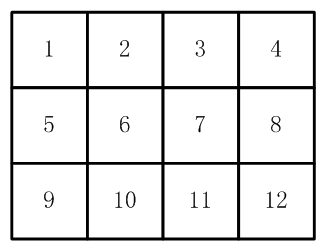

![[ADT笔记]图(graph)](https://img-blog.csdnimg.cn/6d6a9250b0e142cf80f2adb585b9f4b2.png#pic_center)