兔八哥与猎人

题目描述

兔八哥躲藏在树林旁边的果园里。果园有 $M\times N$ 棵树，组成一个 $M$ 行 $N$ 列的矩阵，水平或垂直相邻的两棵树的距离为 $1$。兔八哥在一棵果树下。

猎人背着猎枪走进了果园，他爬上一棵果树，准备杀死兔八哥。

如果猎人与兔八哥之间没有其它的果树，猎人就可以看到兔八哥。

现己知猎人和兔八哥的位置，编写程序判断兔子所在的位置是否安全.

输入格式

第一行为 $n$，表示有 $n$ 组数据，每组数据的第一行为两个正整数 $a_x$ 和 $a_y$，表示猎人的位置，第二行为两个正整数 $b_x$ 和 $b_y$，表示兔八哥的位置。

输出格式

共有 $n$ 行，每行为 yes 或 no 表示兔八哥的位置是否安全。

样例 #1

样例输入 #1

1
1 1
1 2

样例输出 #1

no

提示

$1\le n\le 10^5$，$1\le a_x,a_y,b_x,b_y\le 10^8$。

---

根据题意，可以得出猎人与兔子位置分布如下是no

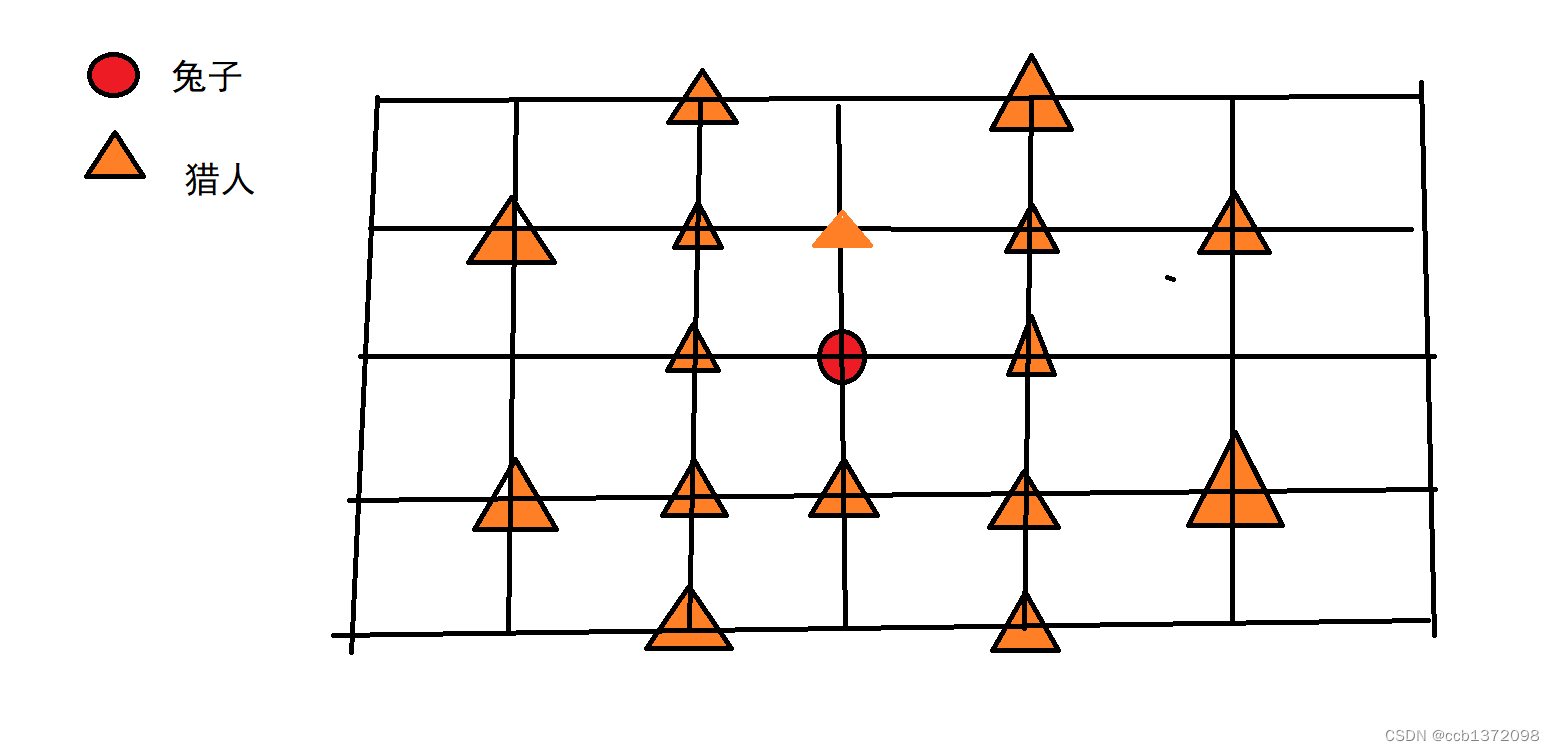
一开始根本没有想到，最外围的三角形也是可以的，只是想到了包围的8个位置。

你会发现如果两个坐标之差的最大公约数为1，那么他们之间就没有整点；

如果不是1，兔子就能存活

#include<bits/stdc++.h>
using namespace std;
int n;
int main()
{cin>>n;
int a,b,c,d;
 for(int i=1;i<=n;i++)
   {cin>>a>>b>>c>>d;
    if(a==c||b==d)
    //特判，排除兔和人在同行或同列的情况，防止__gcd函数出错
      if(abs(a-c)+abs(b-d)<=1) 
       cout<<"no"<<endl;
      else cout<<"yes"<<endl;
      //否则兔子和猎人间至少有一棵树，兔子是安全的
    else if(__gcd(abs(a-c),abs(b-d))==1) cout<<"no"<<endl;
    //判断两点之间的纵坐标之差与横坐标之差是否互质,互质则两点间没有树
         else cout<<"yes"<<endl;//反之人兔间至少有一棵树
   }
return 0;
}