引言
今天带来另一篇激活函数论文SEARCHING FOR ACTIVATION FUNCTIONS的笔记。
作者利用自动搜索技术来发现新的激活函数。通过结合详尽的搜索和基于强化学习的搜索,通过实验发现最佳的激活函数 f ( x ) = x ⋅ sigmoid ( β x ) f(x) = x \cdot \text{sigmoid}(βx) f(x)=x⋅sigmoid(βx),作者称为Swish。
如果 β = 1 \beta=1 β=1,就等于上篇笔记中介绍的SiLU。
简介
每个深度网络的核心是一个线性变换,紧接着是一个激活函数 f ( ⋅ ) f(\cdot) f(⋅)。目前,最成功和广泛使用的激活函数是ReLU。
虽然有许多激活函数被提出来替代ReLU,但没有一种能够像ReLU一样得到广泛应用。
在篇工作中,作者使用自动搜索技术来发现新颖的激活函数。专注于寻找新的标量激活函数,即接受一个标量作为输入并输出一个标量,因为标量激活函数可以用来替换ReLU函数而不改变网络架构。通过结合详尽的搜索和基于强化学习的搜索,作者发现了一些表现出有希望性能的新颖激活函数。
作者对最佳发现的激活函数进行了实证评估,发现的最佳激活函数,我们称之为Swish,是 f ( x ) = x ⋅ sigmoid ( β x ) f(x) = x \cdot \text{sigmoid}(βx) f(x)=x⋅sigmoid(βx),其中 β β β是一个常数或可训练的参数。
方法
为了利用搜索技术,必须设计一个包含有潜力的候选激活函数的搜索空间。在设计搜索空间时,平衡搜索空间的大小和表达能力是一个重要的挑战。过于受限的搜索空间不会包含新颖的激活函数,而过大的搜索空间则难以有效搜索。为了平衡这两个标准,祖宗设计了一个简单的搜索空间,该空间通过组合一元和二元函数来构造激活函数。
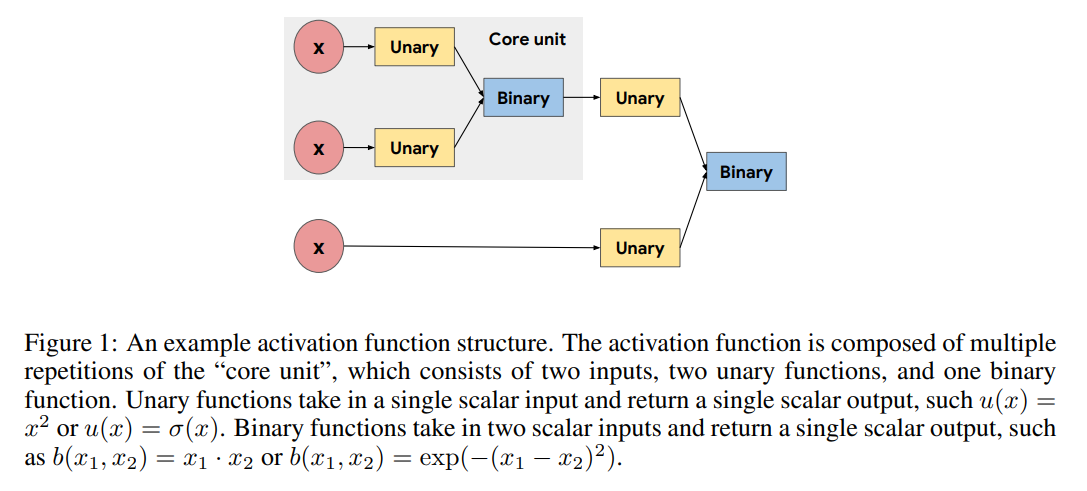
如图1所示,激活函数是通过反复组合core unit(核心单元)构建的,core unit定义为 b ( u 1 ( x 1 ) , u 2 ( x 2 ) ) b(u_1(x_1), u_2(x_2)) b(u1(x1),u2(x2))。核心单元接受两个标量输入,将每个输入独立地通过一元(Unary)函数传递,并使用一个输出标量的二元(Binary)函数将两个一元输出组合起来。由于我们的目标是寻找将单个标量输入转换为单个标量输出的标量激活函数,一元函数的输入受限于层的预激活 x x x和二元函数的输出。
给定搜索空间,搜索算法的目标是找到一元函数和二元函数的有效选择。搜索算法的选择取决于搜索空间的大小。如果搜索空间很小,例如使用单个核心单元,可以穷举搜索整个搜索空间。如果核心单元重复多次,搜索空间将非常大(即大约 1 0 12 10^{12} 1012个可能性),使得穷举搜索变得不可行。

对于大型搜索空间,作者使用一个RNN控制器,如图2所示。在每个时间步,控制器预测激活函数的一个组件。预测结果在下一个时间步骤中反馈给控制器,并重复此过程,直到预测出激活函数的每个组件。然后使用预测的字符串构造激活函数。
一旦搜索算法生成了一个候选的激活函数,就会使用带有候选激活函数的子网络在某个任务上进行训练,例如在CIFAR-10上进行图像分类。训练完成后,记录并使用子网络的验证准确性来更新搜索算法。对于穷举搜索,维护一个根据验证准确性排序的表现最佳的激活函数列表。对于RNN控制器,使用强化学习训练控制器,以最大化验证准确性,其中验证准确性作为奖励。这种训练推动控制器生成具有高验证准确性的激活函数。
由于评估单个激活函数需要训练一个子网络,搜索是计算密集型的。为了减少进行搜索所需的时间,使用分布式训练方案来并行训练每个子网络。在这个方案中,搜索算法提出了一批候选激活函数,将它们添加到一个队列中。工作机器从队列中取出激活函数,训练一个子网络,并报告相应激活函数的最终验证准确性。验证准确性被聚合并用于更新搜索算法。
搜索发现
对于小的搜索空间,使用穷举搜索,而对于更大的搜索空间,使用RNN控制器。RNN控制器使用策略近端优化(Policy Proximal Optimization,PPO)进行训练,使用奖励的指数移动平均作为基准来降低方差。考虑的一元函数和二元函数的完整列表如下:
-
一元函数: x , − x , ∣ x ∣ , x 2 , x 3 , x , β x , x + β , log ( ∣ x ∣ + ϵ ) , exp ( x ) sin ( x ) , cos ( x ) , sinh ( x ) , cosh ( x ) , tanh ( x ) , sinh − 1 ( x ) , tan − 1 ( x ) , sinc ( x ) , max ( x , 0 ) , min ( x , 0 ) , σ ( x ) , log ( 1 + exp ( x ) ) , exp ( − x 2 ) , erf ( x ) , β x,-x,|x|,x^2,x^3,\sqrt x,\beta x, x+\beta,\log(|x|+\epsilon),\exp(x) \sin(x),\cos(x),\sinh(x),\cosh(x),\tanh(x), \sinh^{−1} (x), \tan^{−1} (x), \text{sinc}(x), \max(x, 0), \min(x, 0), σ(x), \log(1 + \exp(x)), \exp(−x^2), \text{erf}(x), β x,−x,∣x∣,x2,x3,x,βx,x+β,log(∣x∣+ϵ),exp(x)sin(x),cos(x),sinh(x),cosh(x),tanh(x),sinh−1(x),tan−1(x),sinc(x),max(x,0),min(x,0),σ(x),log(1+exp(x)),exp(−x2),erf(x),β
-
二元函数: x 1 + x 2 , x 1 ⋅ x 2 , x 1 − x 2 , x 1 x 2 + ϵ , max ( x 1 , x 2 ) , min ( x 1 , x 2 ) , σ ( x 1 ) ⋅ x 2 , exp ( − β ( x 1 − x 2 ) 2 ) , exp ( − β ∣ x 1 − x 2 ∣ ) , β x 1 + ( 1 − β ) x 2 x_1 + x_2, x_1 \cdot x_2, x_1 − x_2, \frac{x_1} {x_2+ \epsilon}, \max(x_1, x_2), \min(x_1, x_2), σ(x_1)\cdot x_2, \exp(−β(x_1 − x_2)^2 ), \exp(−β|x_1 − x_2|), βx_1 + (1 − β)x_2 x1+x2,x1⋅x2,x1−x2,x2+ϵx1,max(x1,x2),min(x1,x2),σ(x1)⋅x2,exp(−β(x1−x2)2),exp(−β∣x1−x2∣),βx1+(1−β)x2
其中 β β β表示每个通道可训练的参数 , σ ( x ) = ( 1 + exp ( − x ) ) − 1 ,σ(x) = (1 + \exp(−x))^{−1} ,σ(x)=(1+exp(−x))−1是sigmoid函数。通过改变用于构建激活函数的核心单元的数量以及改变一元函数和二元函数对搜索算法的可用性,可以创建不同的搜索空间。图3绘制了搜索发现的表现最佳的新颖激活函数。
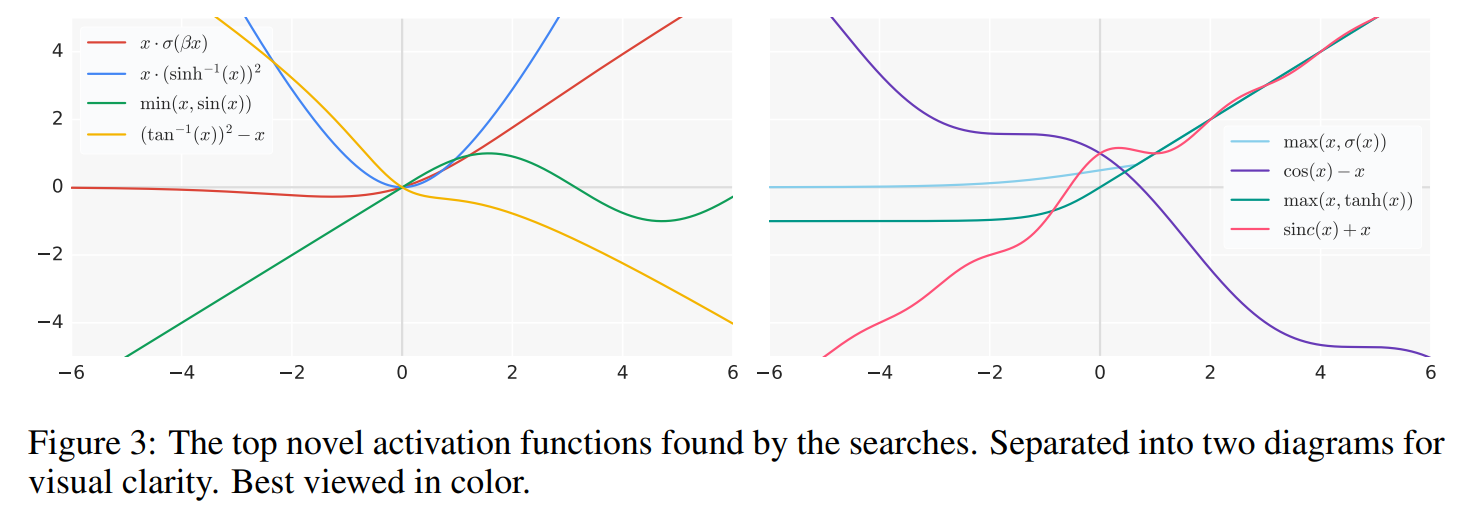
作者强调了搜索发现的几个值得注意的趋势:
-
复杂的激活函数在性能上一直不如简单的激活函数,可能是由于在优化过程中增加了困难。表现最佳的激活函数可以由1个或2个核心单元表示。
-
最佳激活函数共享的一个常见结构是将原始预激活 x x x作为最终二元函数的输入: b ( x , g ( x ) ) b(x, g(x)) b(x,g(x))。ReLU函数也遵循这种结构,其中 b ( x 1 , x 2 ) = max ( x 1 , x 2 ) b(x_1, x_2) = \max(x_1, x_2) b(x1,x2)=max(x1,x2), g ( x ) = 0 g(x) = 0 g(x)=0。
-
搜索发现了利用周期函数(如sin和cos)的激活函数。周期函数的最常见用法是与原始预激活 x x x(或线性缩放的x)相加或相减。在以前的研究中,周期函数在激活函数中的应用只有简单探索,所以这些发现的函数为进一步研究提供了有价值的路径。
-
使用除法的函数通常表现不佳,因为当分母接近0时,输出会变得非常大。除法只有在分母中的函数远离0时才成功,例如 cosh ( x ) \cosh(x) cosh(x),或者当分子接近0时分母也接近0,产生输出为1。
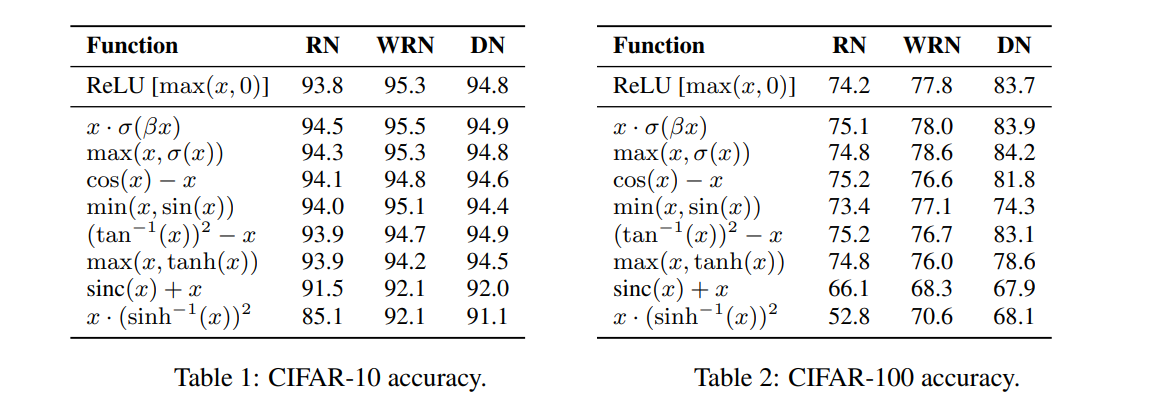
实验结果显示在表1和表2中。尽管模型架构发生了变化,其中六个激活函数成功地进行了泛化。在这六个激活函数中,所有的都与或优于ResNet-164上的ReLU。此外,两个发现的激活函数, x ⋅ σ ( β x ) x\cdotσ(βx) x⋅σ(βx)和 m a x ( x , σ ( x ) ) max(x, σ(x)) max(x,σ(x))在所有三个模型上一直与或优于ReLU。
为了验证搜索的有效性,在本文的其余部分,作者将重点对激活函数 f ( x ) = x ⋅ σ ( β x ) f(x) = x · σ(βx) f(x)=x⋅σ(βx)进行实证评估,称之为Swish。选择广泛评估Swish而不是 m a x ( x , σ ( x ) ) max(x, σ(x)) max(x,σ(x)),因为早期实验表明Swish具有更好的泛化性能。
SWISH
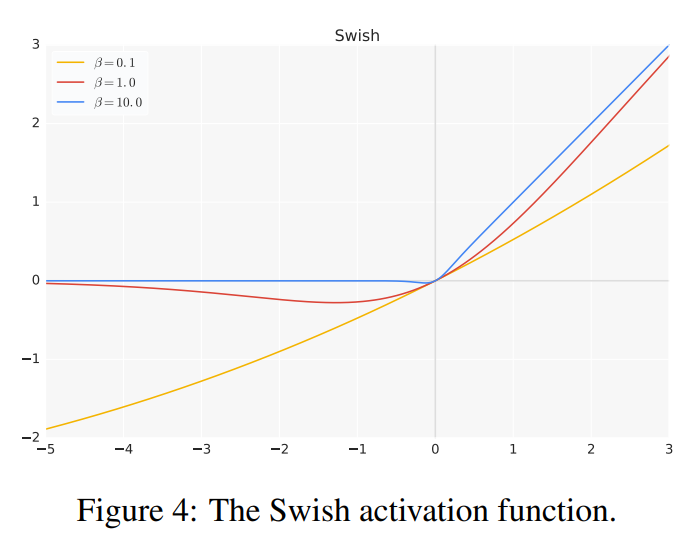
Swish被定义为 x ⋅ σ ( β x ) x \cdot σ(βx) x⋅σ(βx),其中 σ ( z ) = ( 1 + exp ( − z ) ) − 1 σ(z) = (1 + \exp(−z))^{−1} σ(z)=(1+exp(−z))−1是sigmoid函数, β β β可以是一个常数或可训练参数。图4绘制了不同 β β β值下Swish的图形。如果 β = 1 β = 1 β=1,则Swish等同于Elfwing等人提出的用于强化学习的Sigmoid加权线性单元SiL。
如果 β = 0 β = 0 β=0,则Swish变为缩放的线性函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2。当 β → ∞ β → ∞ β→∞时,sigmoid部分逐渐趋近于0-1函数,因此Swish变得类似于ReLU函数。
这表明Swish可以被粗略地视为一个平滑的函数,它在线性函数和ReLU函数之间进行非线性插值。插值的程度可以通过将
β
β
β设置为可训练参数来控制。与ReLU类似,Swish在上方是无界的,在下方是有界的。与ReLU不同,Swish是平滑且非单调的。事实上,Swish的非单调性使其与大多数常见的激活函数有所区别。Swish的导数是
f
′
(
x
)
=
σ
(
β
x
)
+
β
x
⋅
σ
(
β
x
)
(
1
−
σ
(
β
x
)
)
=
σ
(
β
x
)
+
β
x
⋅
σ
(
β
x
)
−
β
x
⋅
σ
(
β
x
)
2
=
β
x
⋅
σ
(
x
)
+
σ
(
β
x
)
(
1
−
β
x
⋅
σ
(
β
x
)
)
=
β
f
(
x
)
+
σ
(
β
x
)
(
1
−
β
f
(
x
)
)
\begin{aligned} f^\prime(x) &= \sigma(\beta x) + \beta x \cdot \sigma (\beta x)(1-\sigma(\beta x)) \\ &= \sigma(\beta x) + \beta x \cdot \sigma (\beta x) - \beta x \cdot \sigma(\beta x)^2 \\ &= \beta x \cdot \sigma (x) + \sigma (\beta x) (1 -\beta x \cdot \sigma (\beta x)) \\ &= \beta f(x) + \sigma(\beta x)(1- \beta f(x)) \end{aligned}
f′(x)=σ(βx)+βx⋅σ(βx)(1−σ(βx))=σ(βx)+βx⋅σ(βx)−βx⋅σ(βx)2=βx⋅σ(x)+σ(βx)(1−βx⋅σ(βx))=βf(x)+σ(βx)(1−βf(x))
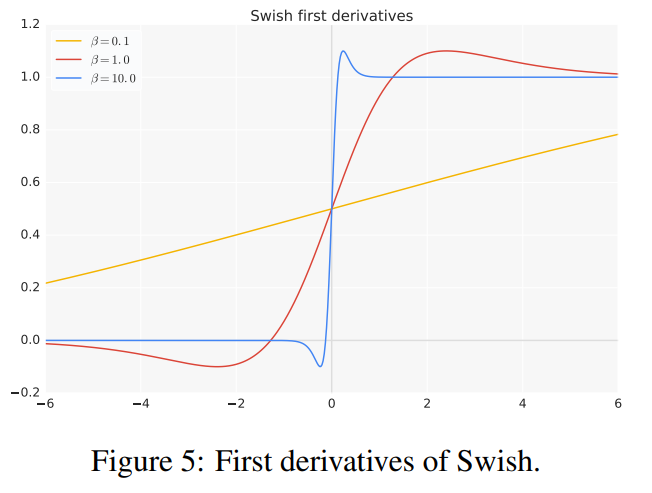
Swish的一阶导数在不同 β β β值下如图5所示。 β β β的值控制着一阶导数趋近于0和1的速度。当 β = 1 β = 1 β=1时,对于小于约1.25的输入,导数的大小小于1。因此,Swish在 β = 1 β = 1 β=1时的成功表明,在现代架构中,ReLU的梯度保持特性(即当 x > 0 x > 0 x>0时导数为1)可能不再是一个明显的优势。
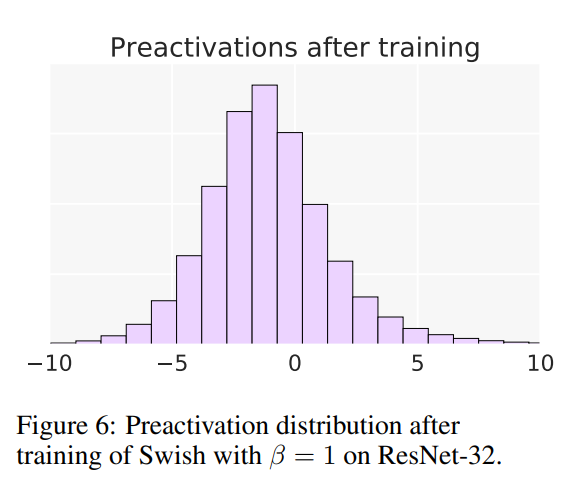
Swish与ReLU之间最显著的区别是当 x < 0 x < 0 x<0时Swish的非单调“凸起”。如图6所示,大部分的预激活值落在凸起的范围内(-5 ≤ x ≤ 0),这表明非单调凸起是Swish的一个重要特性。凸起的形状可以通过改变 β β β参数来控制。虽然在实践中固定 β = 1 β = 1 β=1是有效的,但实验部分显示训练 β β β可以进一步提高某些模型的性能。
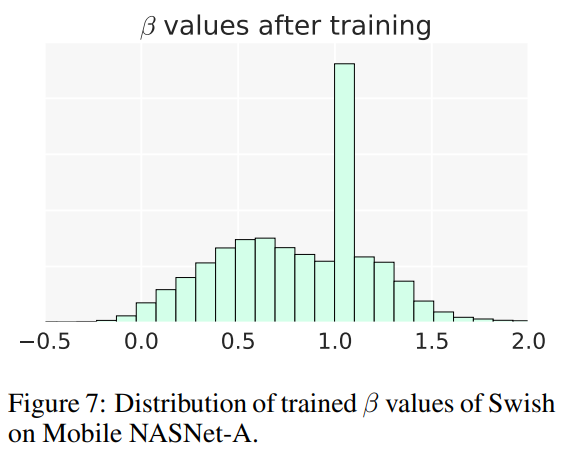
图7显示了从Mobile NASNet-A模型训练得到的
β
β
β值的分布情况。训练得到的
β
β
β值在0和1.5之间分布,并且在
β
≈
1
β ≈ 1
β≈1处有一个峰值,这表明模型利用了可训练
β
β
β参数的额外灵活性。在实际中,Swish可以在大多数深度学习库中通过一行代码的修改来实现,如TensorFlow中的x * tf.sigmoid(beta * x)或tf.nn.swish(x)。
需要注意的是,如果使用BatchNorm,应设置scale参数。由于ReLU函数是分段线性的,一些高级库默认关闭了scale参数,但对于Swish来说,此设置是不正确的。对于训练Swish网络,作者发现略微降低用于训练ReLU网络的学习率效果很好。
实验
略
结论
Swish是通过使用多种自动搜索技术找到的。
Swish在深度模型上始终优于ReLU。Swish的强大性能挑战了关于ReLU的传统观点。当残差连接(He等人,2016a)使得非常深的网络可以优化时,ReLU保持梯度的重要性假设似乎是不必要的。在完全注意力机制的Transformer中可以找到类似的见解。
总结
⭐ 作者利用自动搜索技术来发现新的激活函数。并且通过实验发现最佳的激活函数为 f ( x ) = x ⋅ sigmoid ( β x ) f(x) = x \cdot \text{sigmoid}(βx) f(x)=x⋅sigmoid(βx),称为Swish。







![[NeurIPS-23] GOHA: Generalizable One-shot 3D Neural Head Avatar](https://img-blog.csdnimg.cn/direct/09eaf0f8743d4a339a2e61f83194003b.png)