ROC曲线分析是用于评估一个因素预测能力的手段，是可以用于连续型变量分组的方法。在生存分析中，疾病状态和因素取值均会随时间发生变化。而标准的ROC曲线分析将个体的疾病状态和因素取值视作固定值，未将时间因素考虑在分析之中。在这种情况下，使用时间依赖性ROC无疑是更好的选择

今天咱们视频来演示一下时间依赖ROC曲线绘制

代码

library(survival)
library("survminer")
library(foreign)
#公众号：零基础说科研
#公众号回复：乳腺癌，可以获得这个数据
bc <- read.spss("E:/r/test/Breast cancer survival agec.sav",
                use.value.labels=F, to.data.frame=T)
bc <- na.omit(bc)
names(bc)
##分类变量转成因子
bc$histgrad<-as.factor(bc$histgrad)
bc$er<-as.factor(bc$er)
bc$pr<-as.factor(bc$pr)
bc$ln_yesno<-as.factor(bc$ln_yesno)

f1<-coxph(Surv(time,status)~er+histgrad+pr+age+ln_yesno,bc,x=TRUE,y=TRUE)
f2<-coxph(Surv(time,status)~er+histgrad+ln_yesno,bc,x=TRUE,y=TRUE)
f3<-coxph(Surv(time,status)~ln_yesno,bc,x=TRUE,y=TRUE)

library(riskRegression)
A3<- riskRegression::Score(list("f1"=f1),
                           formula=Surv(time,status)~1,
                           data=bc,
                           metrics="auc",
                           null.model=F,
                           times=seq(3,132,1))
plotAUC(A3)
##########
auc<-plotAUC(A3)
ggplot()+geom_line(data=auc, aes(times,AUC),linetype=1,size=1,alpha = 0.6,colour="red")+
  geom_ribbon(data=auc, aes(times,ymin = lower, ymax = upper),alpha = 0.1,fill="red")+
  geom_hline(yintercept=1, linetype=2,size=1)+theme_classic()+ 
  labs(title = "时间相关性ROC", x="times", y="AUC")

A3<- riskRegression::Score(list("f1"=f1,"f2"=f2),
                           formula=Surv(time,status)~1,
                           data=bc,
                           metrics="AUC",
                           null.model=F,
                           times=seq(3,132,1))
plotAUC(A3)
auc<-plotAUC(A3)
ggplot()+geom_line(data=auc, aes(times,AUC,group=model,col=model))+
  geom_ribbon(data=auc, aes(times,ymin = lower, ymax = upper,fill=model),alpha = 0.1)+
  geom_hline(yintercept=1, linetype=2,size=1)+theme_classic()+ 
  labs(title = "时间相关性ROC", x="times", y="AUC")
###########
library(pec)
A1<-pec::cindex(list("f1"=f1),
                formula=Surv(time,status)~er+histgrad+pr+age+ln_yesno,
                data=bc,
                eval.times=seq(3,132,1))
plot(A1)

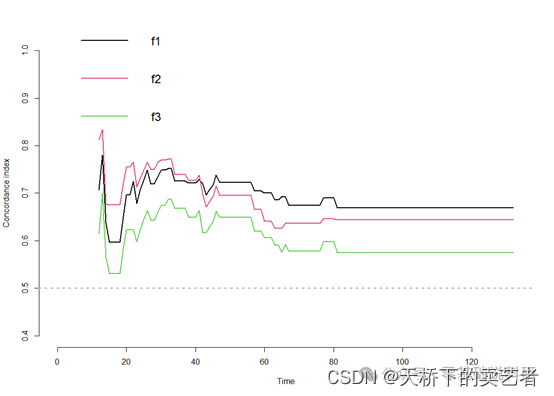
A1<-pec::cindex(list("f1"=f1,"f2"=f2,"f3"=f3),
                formula=Surv(time,status)~er+histgrad+pr+age+ln_yesno,
                data=bc,
                eval.times=seq(3,132,1))
plot(A1)