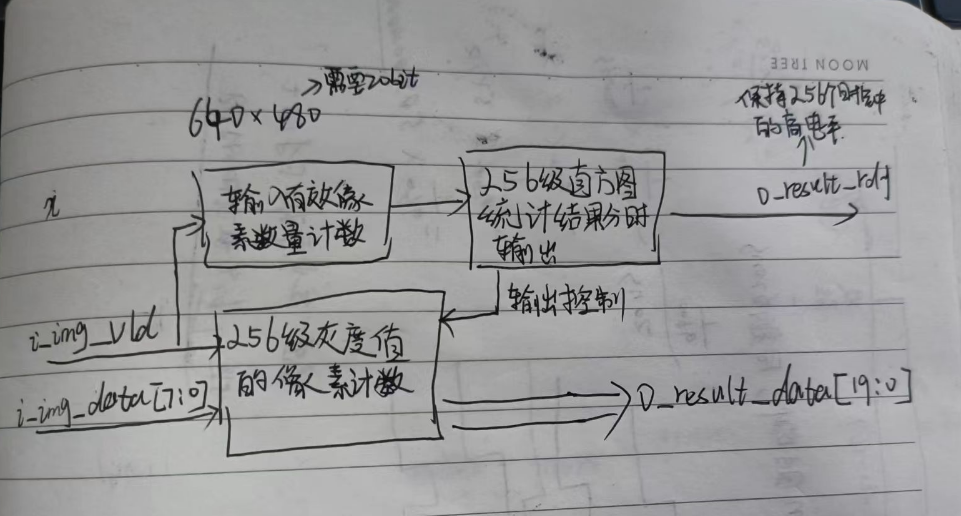
matlab求时间序列的时间滞后相关性

自相关、互相关、加权相关、滞后相关等相关性分析,在时间序列分析中经常被用到,可以量化两个时间序列的相关程度,特别对于有季节性趋势的序列中这个分析尤为必要。下面介绍一个Matlab函数,用于进行相关性分析,具体可在Matlab命令行输入help xcorr查看。
Matlab中用于计算信号的自相关或者互相关的函数是xcorr,该函数的使用方式如下:
% 有以下可调用形式
r = xcorr(x,y) % 两离散序列互相关
r = xcorr(x) % 序列自相关
[R,lags] = xcorr(x,y,maxlags) % 时间滞后相关
x和y是待计算自相关或者互相关的信号序列,maxlags是最大的延迟时间(可以是正值或负值)。函数返回的R是相关系数,lags是对应的延时时间。
下面是一些xcorr函数的示例:
- 计算两个信号
x和y的自相关:
x = randn(1,100); % 生成长度为100的随机信号
[R,lags] = xcorr(x,x,'coeff');
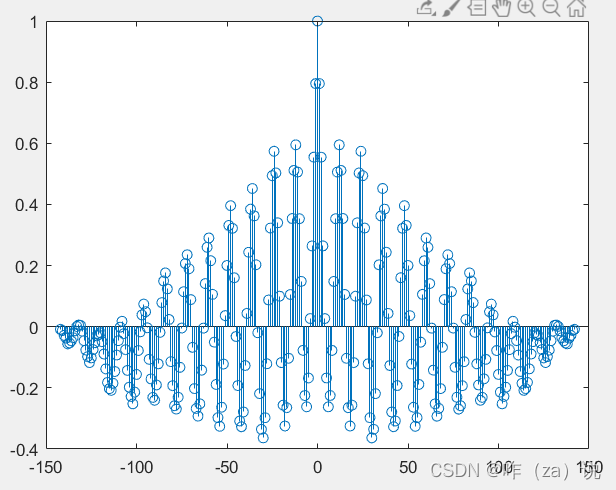
stem(lags,R); % 绘制自相关系数图

从图中可以看出平移量是0时候相关性最大,其它均未表现出相关性,说明序列有极大随机性。用一组带有季节周期性的序列为例,看看效果,能看出移动量为周期的整数倍时相关系数相对较大,半周期是有较大负相关。
- 计算两个信号
x和y的互相关:
% 生成示例数据
x = randn(1, 100); % 第一个时间序列
y = circshift(x, 10); % 第二个时间序列,向右移动10个位置
lags = -50:50; % 设置时间滞后范围
% 计算时间滞后相关性
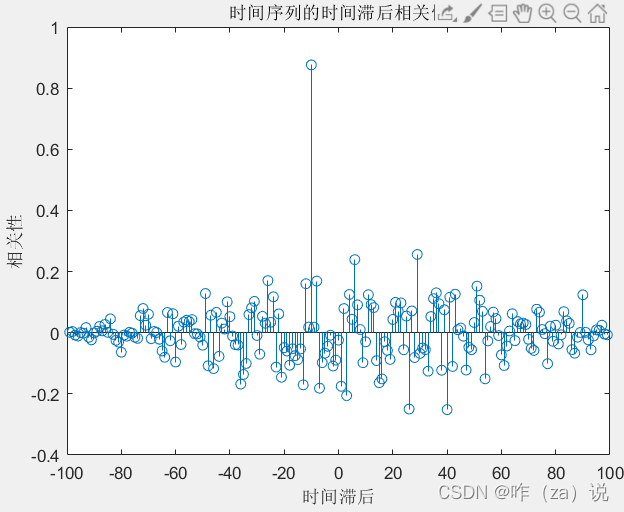
[c, lags] = xcorr(x, y, 'coeff');
% 画出时间滞后相关性图
stem(lags, c);
xlabel('时间滞后');
ylabel('相关性');
title('时间序列的时间滞后相关性');
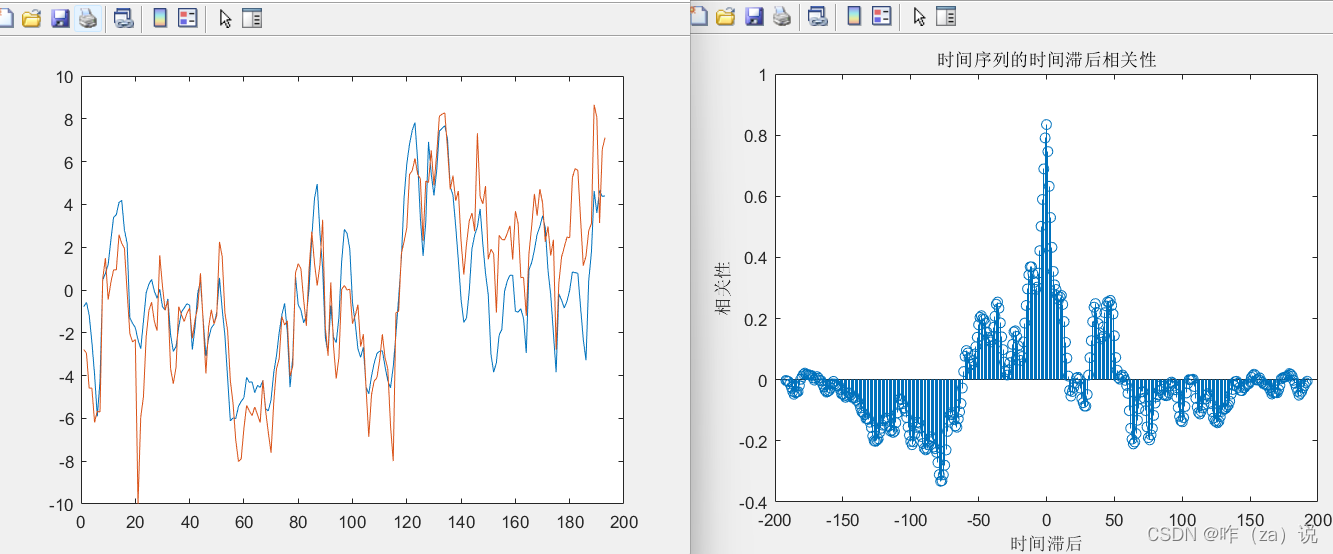
上图是随机数生成的,没趋势、没周期,相关性最大的位置就在序列平移的位置;下面是实际数据出的结果,原两条序列有明显的趋势和周期,对其进行时间滞后分析,从图中可以看出两序列没有滞后性。
xcorr函数还有一些可选参数,可以控制计算的方式,比如'coeff'表示将相关系数标准化在-1和1之间,'biased'表示使用无偏估计。用户可以根据具体需求选择适合的参数。
内容比较简单,在需要的时候可以作为简单参考。