[论文笔记]GAUSSIAN ERROR LINEAR UNITS (GELUS)

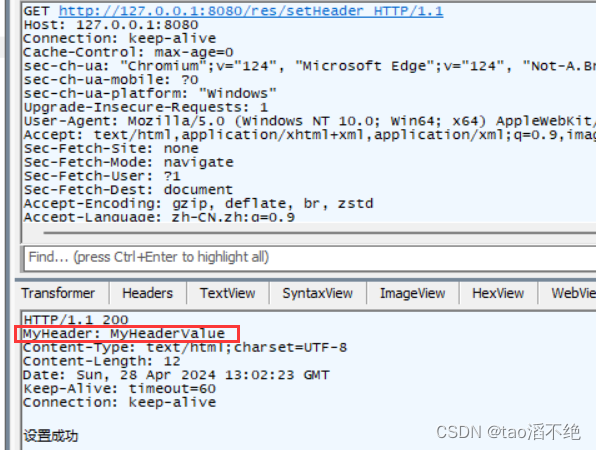
引言

今天来看一下GELU的原始论文。

作者提出了GELU(Gaussian Error Linear Unit,高斯误差线性单元)非线性激活函数： $\text{GELU}= x\Phi(x)$ ，其中 $\Phi(x)$ 是标准高斯累积分布函数。与ReLU激活函数通过输入的符号进行门控不同，GELU非线性激活函数通过输入的数值进行加权。

总体介绍

随着网络变得更深，使用sigmoid激活函数进行训练的效果不如非平滑、非概率性的ReLU，后者基于输入的符号进行硬门控决策。ReLU通常比sigmoid激活函数能够实现更快更好的收敛性。在ReLU的成功基础上，最近的一种修改称为ELU允许ReLU-like的非线性激活函数输出负值，这有时可以提高训练速度。总之，激活函数选择对于神经网络仍然是一个必要的架构决策，否则网络将成为一个深度线性分类器。

深度非线性分类器能够很好地拟合数据，以至于网络设计者通常需要选择是否包含随机正则化器，例如在隐藏层添加噪声或应用dropout，而这个选择与激活函数是相互独立的。因此，非线性和dropout共同决定了神经元的输出，但这两个创新仍然是不同的。此外，由于流行的随机正则化器不考虑输入，而非线性受到这些正则化器的帮助，因此两者都不会取代对方。

在这篇工作中，作者引入了一种新称为GELU的激活函数。它与随机正则化器有关，因为它是自适应dropout修改的期望。这表明了对神经元输出的更概率性的观点。

补充知识

正态分布与误差函数

本节介绍一些相关知识，以便更好地理解这篇论文。正态分布的概率密度函数为：
$\frac{1}{\sqrt{2\pi} \sigma} \exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right) \tag{p1}$
假设 $X$ 是随机变量，累积分布函数是概率 $\leq x)$ ，用概率密度函数可以表示为：
$F(x;\mu,\sigma) = \frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^x \exp\left( -\frac{(t-\mu)^2}{2\sigma^2} \right)dt \tag{p2}$
正态分布可记为 $N(\mu,\sigma^2)$ ，其中 $\mu$ 和 $\sigma^2$ 分别代表均值和方差。当 $\mu=0,\sigma=1$ 时称为标准正态分布。

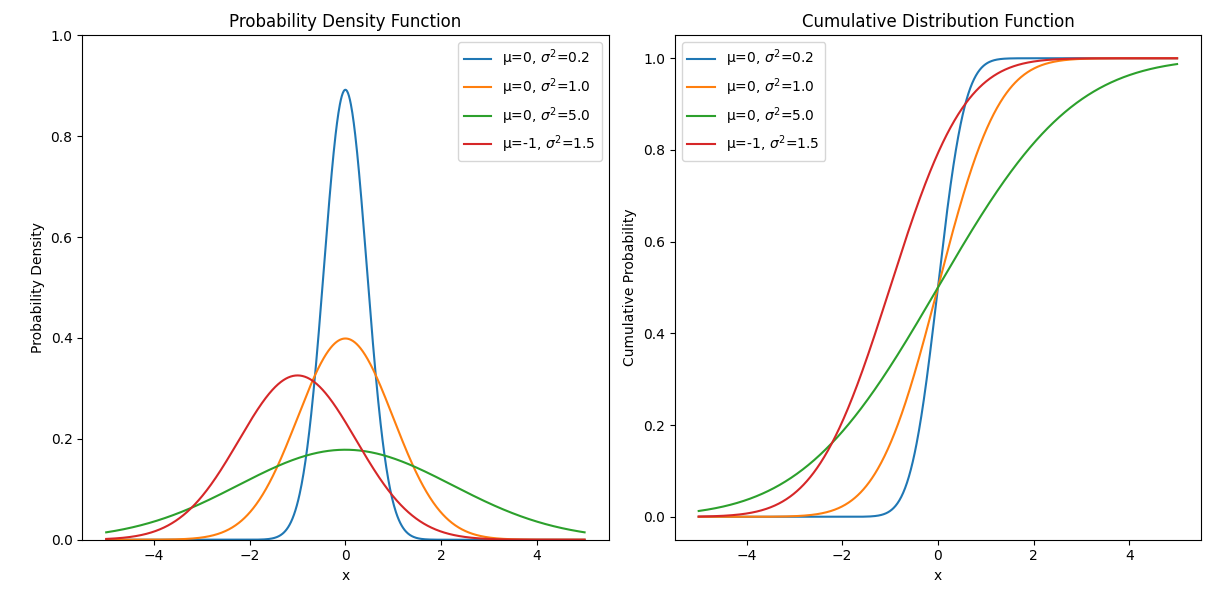
下图是一些不同取值的概率密度函数图像(左)和累积分布函数图像(右)：

误差函数(Error function, $\text{erf}$ )的定义如下：
$\text{erf}(x) = \frac{1}{\sqrt \pi} \int_{-x}^x e^{-t^2} dt = \frac{2}{\sqrt \pi} \int_0^x e^{-t^2} dt \tag{p3}$
互补误差函数( $\text{erfc}$ )，在误差函数的基础上定义：
$\text{erfc} = 1 - \text{erf}(x) = \frac{2}{\sqrt \pi} \int_x^\infty e^{-t^2} dt \tag{p4}$
为什么要介绍误差函数，因为它和正态分布式有关系的，重点是作者也引入了它。

误差函数本质上与标准正态累积分布函数 $\Phi$ (将 $\mu=0,\sigma=1$ 代入式p2)是等价的：
$\Phi(x) =\frac{1}{\sqrt{2\pi}} \int_{-\infty}^x \exp\left( -\frac{t^2}{2} \right)dt = \frac{1}{2}\left[1+ \text{erf}\left( \frac{x}{\sqrt 2}\right) \right ] = \frac{1}{2} \text{erfc} \left(-\frac{x}{\sqrt 2} \right)\tag{p5}$
可整理为如下形式：
$\begin{aligned} \text{erf}(x) &= 2\Phi(x\sqrt 2) -1 \\ \text{erfc}(x) &= 2\Phi(-x\sqrt 2) = 2(1-\Phi(x\sqrt 2)) \end{aligned}$

关于泰勒展开可以参考——人工智能数学基础之高等数学。

误差函数泰勒展开收敛：
$\text{erf}(z) = \frac{2}{\sqrt \pi} \sum_{n=0}^\infty \frac{(-1)^n z^{2n+1}}{n!(2n+1)} =\frac{2}{\sqrt \pi} \left(z - \frac{z^3}{3} + \frac{z^5}{10} - \frac{z^7}{42} + \frac{z^9}{216} - \cdots \right) \tag{p6}$
误差函数和 $\tanh$ 的关系：
$\text{erf}(x) \approx \tanh\left(\frac{2}{\sqrt \pi} \left(x +\frac{11}{123}x^3 \right) \right) \tag{p7}$

import numpy as np
import matplotlib.pyplot as plt
import scipy.special

x = np.linspace(-3, 3, 100)

y1 = scipy.special.erf(x)

y2 = np.tanh(2/np.sqrt(np.pi)*(x + 11/123 * x**3))

plt.figure()
plt.plot(x, y1, label='erf(x)')
plt.plot(x, y2, label='tanh(x)')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Plot of erf(x) and tanh(x)')
plt.legend()
plt.grid(True)
plt.show()

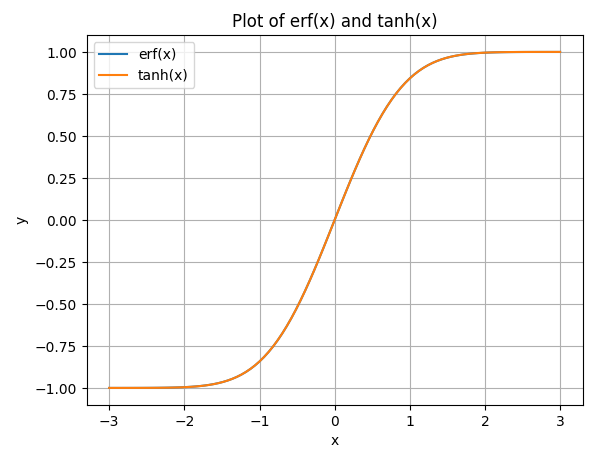
当通常如上代码画图，这两个函数的图几乎重叠。

伯努利分布

伯努利分布(Bernoulli distribution)，又称为两点分布或0-1分布，是一个离散型概率分布。若伯努利试验成功，则伯努利随机变量取值为1，否则伯努利试验失败，伯努利随机变量取值为0。即其成功概率为 $\leq p \leq 1)$ ，失败概率为 $q = 1 - p$ 。

其概率质量函数(probability mass function, pmf)为：
$f_X(x) = p^x (1-p)^{1-x} = \begin{cases} p & \text{if x = 1}\\ q & \text{if x = 0} \end{cases}$
概率质量函数是离散型随机变量在各特定取值上的概率，和概率密度函数的一个不同之处在于：概率质量函数是对离散随机变量定义的，本身代表该值的概率；概率密度函数本身不是概率，只有对连续随机变量的概率密度函数必须在某一个区间内被积分后才能产生出概率。

不同成功概率下的概率质量函数图像：

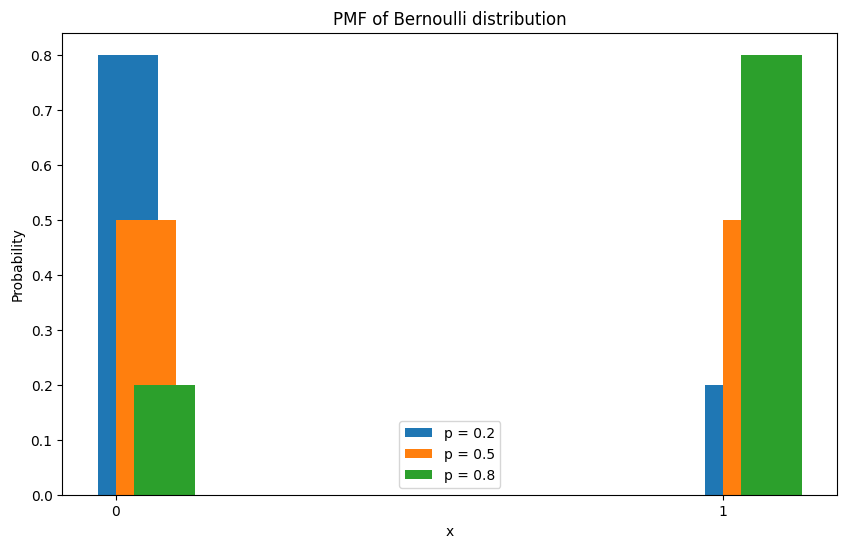
其期望为：
$\sum_{i=0}^1 x_i f_X(x) = 0 + p = p \tag {p6}$

GELU公式

作者通过结合dropout、zoneout和ReLU的特性来激发出这个激活函数。

首先要注意的是，ReLU和dropout都可以确定地将神经元的输出乘零或一，而dropout则是随机地将其乘零。此外，一种新的RNN正则化器称为zoneout可以通过乘一来随机地乘输入。

作者通过将输入乘零或一来合并这种功能，但是这个零一掩码的值是随机确定的，同时也依赖于输入。具体来说，将神经元的输入 $x$ 乘 $\text{Bernoulli}(\Phi(x))$ ，其中 $\Phi(x) = P(X ≤ x)$ ， $X \sim N (0, 1)$ 是标准正态分布的累积分布函数。

选择这个分布是因为神经元的输入往往遵循正态分布，尤其是在批归一化的情况下。在这种情况下，随着 $x$ 的减小，输入“被丢弃”的概率更高，因此应用于 $x$ 的转换是随机的，但取决于输入。

以这种方式屏蔽输入保留了非确定性，但仍然依赖于输入值。随机选择的掩码相当于对输入进行随机的恒等映射(不变)和置零映射。这非常类似于自适应dropout，但自适应dropout与非线性一起使用，并使用逻辑斯蒂分布而不是标准正态分布。作者发现，只使用这种随机正则化器就可以训练出具有竞争力的网络，而不需要使用任何非线性。

我们通常希望神经网络做出确定性的决策，所以激活函数的输出应该是确定的，不能是随机的。为了移除这个随机性，我们可以计算期望：
$x\Phi(x)$
因为 $m$ 是伯努利分布，根据(p6)我们知道该伯努利分布的期望为 $\Phi(x)$ 。

由于高斯分布的累积分布函数通常使用误差函数计算，因此作者将GELU定义为：
$\text{GELU} (x) = x P(X \leq x) = x\Phi(x) = x \cdot \frac{1}{2} \left[1 + \text{erf}(x / \sqrt 2) \right]$
这里可以参考(p5)。

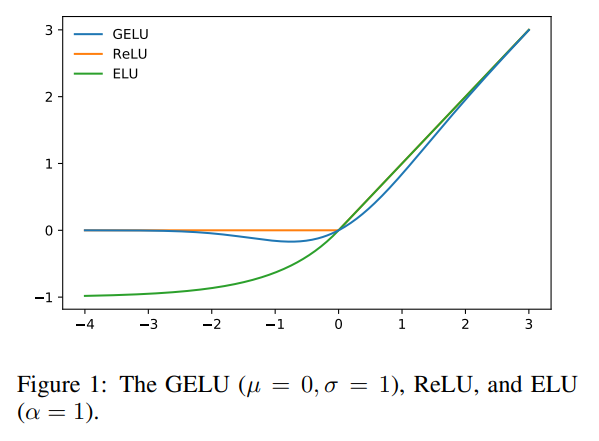
其对应的函数图像可以参考上图的蓝线。从其图像可以看出，在负值区域，不像 $\text{ReLU}$ 全为0，并且是光滑地、处处可导的。

在HuggingFace的transformers库中的实现为如下：

class GELUActivation(nn.Module):
    """
    Original Implementation of the GELU activation function in Google BERT repo when initially created. For
    information: OpenAI GPT's GELU is slightly different (and gives slightly different results): 0.5 * x * (1 +
    torch.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * torch.pow(x, 3)))) This is now written in C in nn.functional
    Also see the Gaussian Error Linear Units paper: https://arxiv.org/abs/1606.08415
    """

    def __init__(self, use_gelu_python: bool = False):
        super().__init__()
        if use_gelu_python:
            self.act = self._gelu_python
        else:
            self.act = nn.functional.gelu

    def _gelu_python(self, input: Tensor) -> Tensor:
        return input * 0.5 * (1.0 + torch.erf(input / math.sqrt(2.0)))

    def forward(self, input: Tensor) -> Tensor:
        return self.act(input)

可以看到这里提供了两种实现，一种是直接通过上面的公式实现——_gelu_python()；从注释中可以看出，还有一种是基于0.5 * x * (1 +torch.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * torch.pow(x, 3))))的近似实现，通过C来实现，默认是采用这种方式。

后者是为了加速计算，第一种实现时精确求解。作者有指出可以近似GELU为
$\tanh[\sqrt{2/\pi} (x + 0.044715x^3)])$

或
$x\sigma(1.702 x)$
甚至如果更快的前馈网络速度的价值超过了准确性的代价，还可以使用不同的累积分布函数。例如，我们可以使用逻辑斯蒂分布的累积分布函数 $σ (x)$ 来得到所谓的Sigmoid线性单元(Sigmoid Linear Unit, SiLU)：
$\text{SiLU} = x\sigma(x)$
也可以使用 $N(\mu, σ^2)$ 的累积分布函数，并让µ和σ成为可学习的超参数，但在这项工作中，只简单地让 $\mu= 0$ 和 $σ = 1$ 。

近似推导

从补充知识中我们看到了 $\text{erf}(x) \approx \tanh\left(\frac{2}{\sqrt \pi} \left(x +\frac{11}{123}x^3 \right) \right)$ 。下面我们利用泰勒展开证明一下。

$\tanh x$ 的泰勒展开为：
$\tanh x = \sum^{\infty}_{n=1} \frac{2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}= x -\frac{x^3}{3} + \frac{2x^5}{15} - \frac{17x^7}{315} + \cdots$
假设我们不知道式(p7)中的具体数值。我们考虑近似形式 $tanh (ax+bx^3)$ 以及 $\text{GELU}$ 中的形式，在 $x = 0$ 处展开

考虑 $tanh (ax+bx^3)$ 的泰勒展开：
$bx^3 - (\frac{a^3}{3}x^3 + \frac{b^3x^6}{3}) + \cdots$
我们仅考虑前两项，即令同幂次前的系数相等：
$\text{erf}(\frac{x}{\sqrt 2}) - \tanh(ax+bx^3) = \left( \sqrt \frac{ 2}{ \pi} -a \right)x +\left(\frac{a^3}{3} -b -\frac{1}{3\sqrt {2\pi}} \right)x^3$
得到两个方程，求解得到

$\sqrt \frac{2}{\pi},\quad b=\frac{4-\pi}{3\sqrt 2\pi^{3/2}}$

代入GELU中的 $x\Phi(x)$ ，得到

$\begin{equation}x\Phi(x)\approx \frac{1}{2} x\left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.0455399 x^3\right)\right)\right]\end{equation}$

这个值很接近 $0.044715$ ，因为我们仅做了前两项的近似，所以得到的这个值与真实值存在误差，注意的是作者提出的也是一种近似，也存在误差。这种做法仅考虑局部误差，即在 $x = 0$ 的局部会比较精确。

因此我们还需要考虑全局误差。

我们固定 $a=\sqrt{\frac{2}{\pi}}$ ，这个 $a$ 是一阶局部近似，我们希望保留在这个近似。同时希望 $b$ 尽可能帮我们减少全局误差。所以我们可以求解：
$\begin{equation}\min_{b} \max_x \left|\text{erf}\left(\frac{x}{\sqrt{2}}\right)-\tanh\left(a x + b x^3\right)\right|\end{equation}$
通过参考2中给出的代码来求解：

import numpy as np
from scipy.special import erf
from scipy.optimize import minimize
# 增加设置显示精度
np.set_printoptions(precision=20)

def f(x, b):
    a = np.sqrt(2 / np.pi)
    return np.abs(erf(x / np.sqrt(2)) - np.tanh(a * x + b * x**3))

def g(b):
    return np.max([f(x, b) for x in np.arange(0, 4, 0.001)])

options = {'xtol': 1e-10, 'ftol': 1e-10, 'maxiter': 100000}
result = minimize(g, 0, method='Powell', options=options)
print(result.x)

[0.035677337314877496]

代入 $x\Phi(x)$ ，得到：

$\begin{equation}x\Phi(x)\approx \frac{1}{2} x\left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.04471491123850979 x^3\right)\right)\right]\end{equation}$

怎么代入呢，因为上式提出了一个 $\sqrt{\frac{2}{\pi}}$ ，所以让 $0.035677337314877496 \times \sqrt \frac{\pi}{2}$ 即可：

import math

math.sqrt(math.pi /2) * 0.035677337314877496

0.04471491123850979

此时得到的结果比论文中的 $0.044715$ 更加精确。

本篇工作中还提出了一种近似，即 $x\sigma(1.702 x)$ ，它是直接用 $\sigma(bx)$ 全局逼近 $\Phi(x)$ 的结果，即
$\begin{equation}\min_{\lambda}\max_{x}\left|\Phi(x) - \sigma(b x)\right|\end{equation}$
修改下上面的代码：

import numpy as np
from scipy.special import erf
from scipy.optimize import minimize
from scipy.special import expit


np.set_printoptions(precision=20)

def f(x, b):
    return np.abs(0.5*(1+erf(x / np.sqrt(2))) - 1/(1 + np.exp(-b*x)))

def g(b):
    return np.max([f(x, b) for x in np.arange(0, 4, 0.001)])

options = {'xtol': 1e-10, 'ftol': 1e-10, 'maxiter': 100000}
result = minimize(g, 0, method='Powell', options=options)
print(result.x)

[1.7017449256323682]

即
$\begin{equation}\Phi(x)\approx \sigma(1.7017449256323682 x)\end{equation}$

实验

略

讨论

通过实验证明，GELU表现优于先前的非线性激活函数，但在其他方面与ReLU和ELU相似。例如，当 $σ \to 0$ 且 $\mu = 0$ 时，GELU变成了ReLU。此外，ReLU和GELU在渐进上是相等的。实际上，可以将GELU视为平滑ReLU的一种方式。

GELU和之前的激活函数比有几个显著的区别。这个非凸非单调函数在正域不是线性的，并且在所有点上都表现出曲率。而ReLU和ELU是凸函数和单调激活函数，在正域中是线性的，因此可能缺乏曲率。因此，增加曲率和非单调性可能使GELU比ReLU或ELU更容易逼近复杂的函数。此外，由于 $\text{ReLU}(x) = x\Bbb 1(x > 0)$ 和 $\text{GELU}(x) = x\Phi(x)$ ，如果 $\mu = 0，σ = 1$ ，我们可以看到ReLU根据输入的符号对其进行门控，而GELU根据其相对于其他输入的大小对其进行加权。此外，重要的是指出，GELU具有概率解释，因为它是随机正则化器的期望。