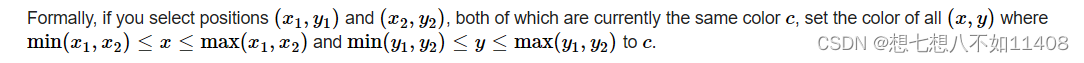A. Card Exchange(思维
Problem - A - Codeforces
题目大意:
给定n张牌,每次选k张相同的牌,把他们变成k-1张任意的牌,求最后手中最少能有几张牌。
思路:
直接判断这n张牌当中有没有k张一样的牌,如果有就一定能变成最后只剩k-1张牌。如果没有k张一模一样的牌,说明一次变化都做不了,最后只能有n张牌。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e6+10;
const int mod=998244353;
int a[N];
std::map<int,int> mp;
void solve()
{
mp.clear();
int n,k;
std::cin>>n>>k;
for(int i=1;i<=n;i++)
{
std::cin>>a[i];
mp[a[i]]++;
}
int flag=0;
for(auto i:mp)
{
if(i.second>=k)
{
flag=1;
break;
}
}
if(flag) std::cout<<k-1<<'\n';
else std::cout<<n<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}B. Rectangle Filling(思维
Problem - B - Codeforces
题目大意:
给定一个n*m的矩形,每次可以选择颜色相同的两个点(x1,y1),(x2,y2)把这俩点之间的所有点都染成这个颜色。试判断输入的矩形能否被染成一种颜色。
思路:
这题我想了好久。。。先想着暴力100次找到最靠右下的与(1,1)颜色相同的点,然后染色,但是不止左上右下可以染色,左下右上也能染色,总之都是错的思路。。。
然后一直感觉四个顶点是最特殊的点,因为顶点后面就没点了,如果顶点能同色就稳了,如果不能就no。其实想到了四个顶点后面就好想了,先判断左上右下和左下右上这两种情况的点的颜色是否相同。相同直接输出yes啊,不相同再分情况讨论。左上和右上相同,那么只要最后一行中有与左上颜色相同的点即可。以此类推,四种情况。

#include<bits/stdc++.h>
using ll=long long;
const int N=500+10;
const int mod=998244353;
int a[N];
char g[N][N];
std::map<char,int> mp;
void solve()
{
int n,m;
std::cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
std::cin>>g[i][j];
}
}
if(g[1][1]==g[n][m]||g[1][m]==g[n][1])
{
std::cout<<"YES"<<'\n';
return ;
}
if(n==1||m==1)
{
std::cout<<"NO"<<'\n';
return ;
}
//判断四个点
if(g[1][1]==g[1][m])//第一行相等
{
for(int i=1;i<=m;i++)
{
if(g[n][i]==g[1][1])
{
std::cout<<"YES"<<'\n';
return ;
}
}
}
if(g[n][1]==g[n][m]){//最后一行相等
for(int i=1;i<=m;i++)
{
if(g[n][1]==g[1][i])
{
std::cout<<"YES"<<'\n';
return ;
}
}
}
if(g[1][m]==g[n][m])//最后一列相等
{
for(int i=1;i<=n;i++)
{
if(g[i][1]==g[1][m])
{
std::cout<<"YES"<<'\n';
return ;
}
}
}
if(g[1][1]==g[n][1]){//第一列相等
for(int i=1;i<=n;i++)
{
if(g[i][m]==g[1][1])
{
std::cout<<"YES"<<'\n';
return ;
}
}
}
std::cout<<"NO"<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}C. Everything Nim(思维
Problem - C - Codeforces
题目大意:
a和b玩游戏,有n堆石子,每次拿走每堆石子中的k个,最后一个拿不了的就输,如果都以最优策略玩游戏输出谁会赢。
思路:
当时一看这不是一眼博弈论最板子的题吗,我还在想cf怎么会有这么板的题。跑了遍样例发现果然不是我想的那样,最后去群里问发现是读错题了。。。每堆都要拿走k个啊。。。
对石子堆去重排序,如果有1234这种连续数的情况,则alice和bob每次都只能取1,如果全部数是12345-》1234(Alice拿完)-》123(bob拿完)-》12(Alice拿完)-》1(bob拿完),
如果是奇数则alice赢,偶数bob赢。
那对于12355这种情况-》1244(Alice拿完)-》133(bob拿完)-》22(alice)拿完-》bob赢,前面是奇数个则轮到bob时能选择怎么操作,如果最后的数字相同bob直接拿完就赢了,如果不相同比如246,都拿一个,135则a就只能被迫拿一个了,24bob再拿一个,13alice又只能被迫拿一个,因此bob必赢。
#include<bits/stdc++.h>
using ll=long long;
const int N=2e5+10;
const int mod=998244353;
int a[N];
void solve()
{
int n;
std::cin>>n;
int k=0;
std::map<int,int> mp;
for(int i=1;i<=n;i++)
{
int x;
std::cin>>x;
if(mp[x]) continue;
a[++k]=x;
mp[x]++;
}
std::sort(a+1,a+1+k);
// for(int i=1;i<=k;i++)
// {
// std::cout<<a[i]<<" ";
// }
int cnt=0;
for(int i=1;i<=k;i++)
{
if(a[i]==a[i-1]+1) cnt++;//有多少个连续的12345
else break;
}
if(cnt==k)
{
if(k%2==1) std::cout<<"Alice"<<'\n';
else std::cout<<"Bob"<<'\n';
}else if(cnt%2==1){//123 33
std::cout<<"Bob"<<'\n';
}else std::cout<<"Alice"<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}D. Missing Subsequence Sum(构造
Problem - D - Codeforces
题目大意:
给定n和k,输出一个序列,对任意i∈[1,k)∪(k,N],这个序列中存在子序列的和为i
思路:
#include<bits/stdc++.h>
using ll=long long;
const int N=1e6+10;
const int mod=998244353;
int f[N];
void solve()
{
int n,k;
std::cin>>n>>k;
std::vector<int> ans;
int q=1;
while(q<=N)
{
ans.push_back(q);
q*=2;
}
int s=0,v=0;
for(int i=0;i<ans.size();i++)
{
s+=ans[i];
if(s>=k)
{
v=ans[i];
ans.erase(ans.begin()+i);
break;
}
}
ans.push_back(k-v);
ans.push_back(k+1+v);
ans.push_back(k+1);
std::cout<<ans.size()<<'\n';
for(auto i:ans)
{
std::cout<<i<<" ";
}
std::cout<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}