常用按时间顺序排列的一组随机变量来表示一个随机事件的时间序列,简记为
用表示该随机序列的n个有序观察值,称之为序列长度为n的观察值序列。
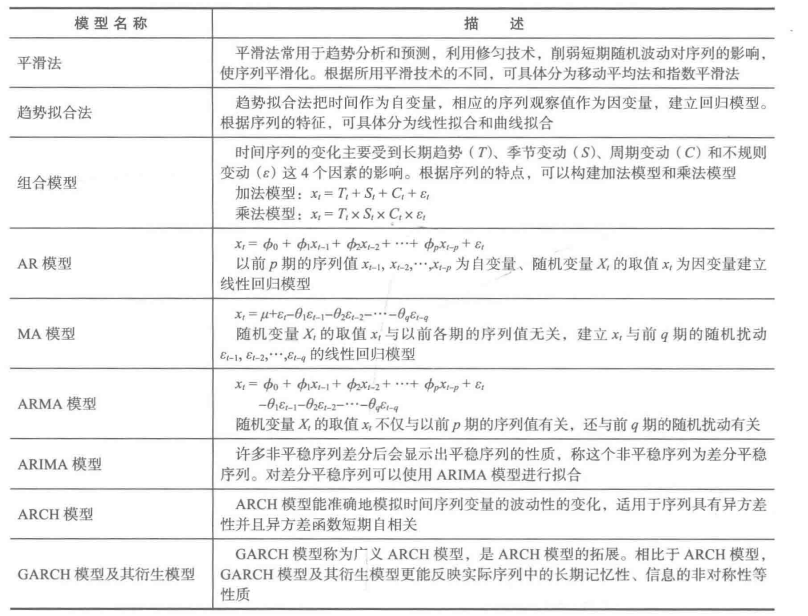
常用的时间序列模型
时间序列的预处理
拿到一个观察值序列后,首先要对它的纯随机性和平稳性进行检验,这两个重要的检验称为序列的预处理。根据检验结果可以将序列分为不同的类型,对不同类型的序列会采取不同的分析方法。
对于纯随机序列,又称为白噪声序列,序列的各项之间没有任何相关关系,序列在进行完全无序的随机波动,可以终止对该序列的分析。白噪声序列是没有信息可提取的平稳序列。
对于平稳非白噪声序列,它的均值和方差是常数,通常是建立一个线性模型来拟合该序列,借此提取该序列的有用信息。ARMA 模型是最常用的平稳序列拟合模型。
对于非平稳序列,由于它的均值和方差不稳定,处理方法一般是将其转变为平稳序列这样就可以应用有关平稳时间序列的分析方法,如建立ARMA模型来进行相应的研究。如果一个时间序列经差分运算后具有平稳性,则该序列为差分平稳序列,可以使用ARIMA模型进行分析。
1.平稳性检验
对序列的平稳性的检验有两种检验方法,一种是根据时序图和自相关图的特征做出判断的图检验,另一种是构造检验统计量进行检验的方法,目前最常用的方法是单位根检验。
1)时序图检验。根据平稳时间序列的均值和方差都为常数的性质,平稳序列的时序图显示该序列值始终在一个常数附近随机波动,而且波动的范围有界;如果有明显的趋势性或者周期性,那它通常不是平稳序列。
2)自相关图检验。平稳序列具有短期相关性,这个性质表明对平稳序列而言通常只有近期的序列值对现时值的影响比较明显,间隔越远的过去值对现时值的影响越小。随着延迟期数k的增加,平稳序列的自相关系数p(延迟k期)会比较快的衰减趋向于零,并在零附近随机波动,而非平稳序列的自相关系数衰减的速度比较慢,这就是利用自相关图进行平稳性检验的标准。
3)单位根检验。单位根检验是指检验序列中是否存在单位根,如果存在就是非平稳时间序列。
2.纯随机性检验
也就是白噪声检验,白噪声序列具有方差齐性和纯随机性的性质,一般是构造检验统计量来检验序列的纯随机性,原假设是该序列为白噪声序列,常用的检验统计量有Q统计量、LB统计量,由样本各延迟期数的自相关系数可以计算得到检验统计量,然后计算出对应的p值,如果p值显著大于显著性水平(显著性水平a一般取0.05),则表示该序列不能拒绝纯随机的原假设,可以停止对该序列的分析。
1.做出假设:
由于序列值之间的变异性是绝对的,而相关性是偶然的,所以假设条件确定如下原假设:
延迟期数小于或等于m期的序列值之间相互独立
备择假设:延迟期数小于或等于m期的序列值之间有相关性。
2.选择检验统计量

平稳时间序列分析
ARMA 模型的全称是自回归移动平均模型,它是目前最常用的拟合平稳序列的模型。它又可以细分为 AR 模型、MA 模型和 ARMA 三大类。都可以看作是多元线性回归模型。
( 一 ) 自回归模型
如果时间序列y是它的前期值和随机项的线性函数,即可表示为:![]() ,为平稳的p阶自回归序列,即为AR(p)。随机项
,为平稳的p阶自回归序列,即为AR(p)。随机项![]() ,与之后变量不相关,
,与之后变量不相关,![]() 时相互独立的白噪声序列,且服从均值为0,方差为
时相互独立的白噪声序列,且服从均值为0,方差为![]() 的正态分布。
的正态分布。
AR(p)模型性质

(二)移动平均模型
如果时间序列 y,是它的当期和前期的随机误差项的线性函数,即可表示为:![]() ,则称该时间序列是q阶移动平均序列,即为MA(q)。移动平均过程无条件平稳。
,则称该时间序列是q阶移动平均序列,即为MA(q)。移动平均过程无条件平稳。
MA(q)模型性质

(三)自回归移动平均模型
如果时间序列 y,是它的当期和前期的随机误差项以及前期值的线性函数,即可表示为:![]() ,则称
,则称![]() 是自回归移动平均模型。ARMA(p,q)模型等价于无穷阶的AR或MA过程。
是自回归移动平均模型。ARMA(p,q)模型等价于无穷阶的AR或MA过程。
ARMA(p,q)性质

平稳时间序列建模
某个时间序列经过预处理,被判定为平稳非白噪声序列,就可以利用ARMA模型进行建模。计算出平稳非白噪声序列的自相关系数和偏自相关系数,再由AR(p)、MA(q)和ARMA(p,q)的自相关系数和偏自相关系数的性质,选择合适的模型。平稳时间序列建模步骤如图所示:

1)计算 ACF 和PACF。先计算非平稳白噪声序列的自相关系数(ACF)和偏自相关系数(PACF)。2)ARMA模型识别。也称为模型定阶,由AR(p)模型、MA(q)和ARMA(p,q)的自相关系数和偏自相关系数的性质,选择合适的模型。识别的原则见下图:
 非平稳时间序列分析
非平稳时间序列分析
对非平稳时间序列的分析方法可以分为确定性因素分解的时序分析和随机时序分析两大类。
确定性因素分解的方法把所有序列的变化都归结为4个因素(长期趋势、季节变动、循环变动和随机波动)的综合影响,其中长期趋势和季节变动的规律性信息通常比较容易提取,而由随机因素导致的波动则非常难确定和分析,对随机信息浪费严重,会导致模型拟合精度不够理想。
随机时序分析法的发展就是为了弥补确定性因素分解方法的不足。根据时间序列的不同特点,随机时序分析可以建立的模型有 ARIMA模型、残差自回归模型、季节模型、异方差模型等。本节重点介绍使用ARIMA模型对非平稳时间序列进行建模的方法。
1.差分运算


![]()
ARIMA模型
差分运算具有强大的确定性信息提取能力,许多非平稳序列差分后会显示出平稳序列的性质这时称这个非平稳序列为差分平稳序列。对差分平稳序列可以使用ARMA模型进行拟合。ARIMA模型的实质就是差分运算与ARMA模型的组合。差分平稳时间序列建模步骤如图所示:

ARIMA模型示例
2015.1.1~ 2015.2.6 某餐厅的销售数据进行建模,数据如下:

1.平稳性检验
画出时序图,代码如下:
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
discfile = 'D:/daily/data1/arima_data.xls'
forecastnum = 5
data = pd.read_excel(discfile, index_col = u'日期')
#时序图
data.plot()
plt.show()运行结果如下:

时序图显示该序列具有明显的单调递增趋势,可以判断为是非平稳序列;
自相关图
#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
偏自相关图
#偏自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(data).show()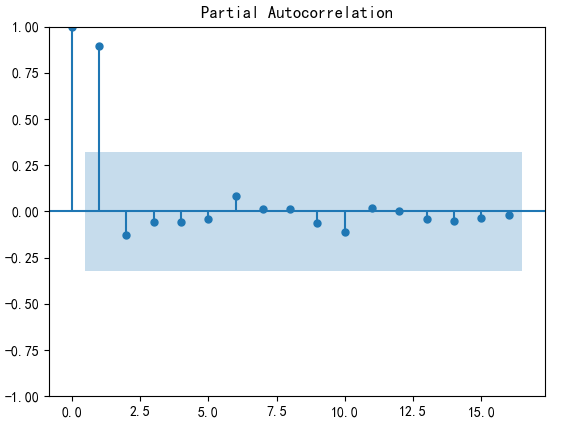
自相关图显示自相关系数长期大于零,说明序列间具有很强的长期相关性;
单位根检验
#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为:', ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
#原始序列的ADF检验结果为: (1.8137710150945276, 0.9983759421514264, 10, 26, {'1%': #-3.7112123008648155, '5%': -2.981246804733728, '10%': -2.6300945562130176}, #299.46989866024177)
单位根检验统计量对应的p值为0.9983759421514264显著大于0.05,最终将该序列判断为非平稳序列(非平稳序列一定不是白噪声序列)。
2.数据差分
下面对原始数据进行一阶差分
#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
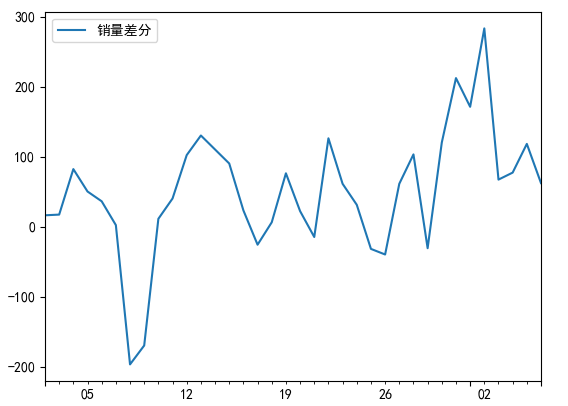
D_data.plot() #时序图
plt.show()差分后的结果如下所示:
自相关图与偏自相关图
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() #偏自相关图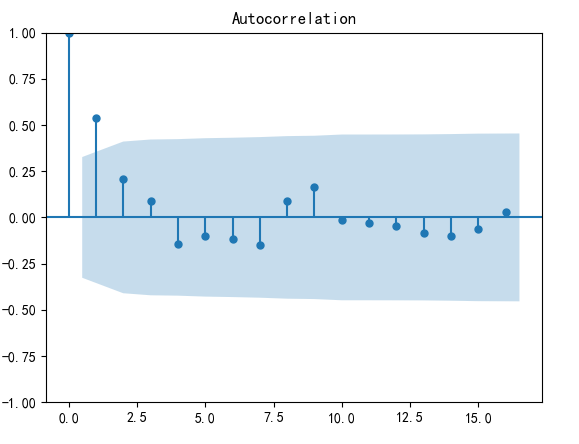
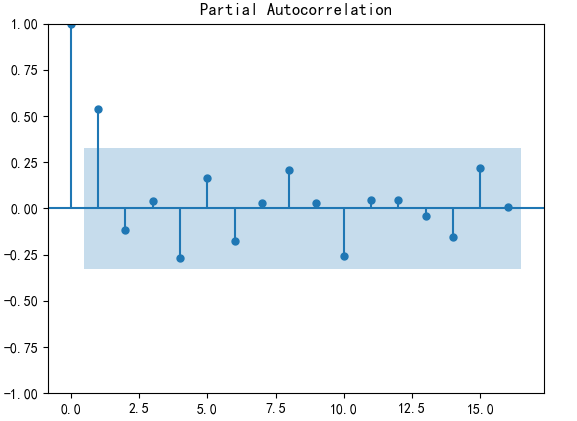
差分后的单位根检验
print(u'差分序列的ADF检验结果为:', ADF(D_data[u'销量差分'])) #平稳性检测
#差分序列的ADF检验结果为: (-3.1560562366723537, 0.022673435440048798, 0, 35, {'1%': #-3.6327426647230316, '5%': -2.9485102040816327, '10%': -2.6130173469387756}, #287.5909090780334)
结果显示,一阶差分之后的序列的时序图在均值附近比较平稳的波动、自相关图有很强的短期相关性、单位根检验对应的p值为0.022673435440048798小于0.05,所以一阶差分之后的序列是平稳序列。
3.白噪声检验
#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为:', acorr_ljungbox(D_data, lags=1)) #返回统计量和p值
from statsmodels.tsa.arima_model import ARIMA
data[u'销量'] = data[u'销量'].astype(float)
#差分序列的白噪声检验结果为: lb_stat lb_pvalue
#1 11.304022 0.000773输出的p值远小于0.05,所以一阶差分之后的序列是平稳非白噪声序列,可以进行后续的建模。
4.模型定阶
方法一:人为识别,一阶差分后自相关图显示出拖尾,偏自相关图显示出1阶截尾,所以可以考虑用MA(1)模型拟合1阶差分后的序列,即对原始序列建立ARIMA(0,1,1)模型。
方法二:相对最优模型识别,计算ARMA(p,q)。当p和q均小于等于3的所有组合的 BIC信息量,取其中BIC信息量达到最小的模型阶数。计算 BIC 矩阵如下。

BIC最小的p值和q值为:1、0
上述代码为:
import pandas as pd
import numpy as np
from statsmodels.tsa.arima.model import ARIMA
import warnings
warnings.filterwarnings("ignore")
data[u'销量'] = data[u'销量'].astype('float64')
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try:
model = ARIMA(data, order=(p, 1, q)).fit()
bic = model.bic
tmp.append(bic)
except:
tmp.append(float('inf')) # 将失败的值替换为无穷大
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix) #将bic矩阵转换为DataFrame
# 找出最小值位置
min_idx = np.unravel_index(np.nanargmin(bic_matrix.values), bic_matrix.shape)
p, q = min_idx
print(u'BIC最小的p值和q值为:%s、%s' %(p, q))
5.建立模型并预测
# 建立ARIMA模型
model = ARIMA(data, order=(p, 1, q)).fit()
print(model.summary())打印模型报告:



预测
# 进行未来5天的预测
forecast_result = model.forecast(steps=5)
print("预测结果:", forecast_result[0])
print("标准误差:", forecast_result[1])
print("置信区间:", forecast_result[2])
# 建立ARIMA模型
model= ARIMA(data, order=(p, 1, q))
print(model.summary())
model_fit=model.fit()
predictions = model_fit.predict(start=len(D_data), end=len(D_data)+5, dynamic=True)
# 绘制拟合曲线
plt.plot(data[u'销量'], label="模型数据")
plt.plot(predictions, label="预测数据")
plt.legend()
plt.show()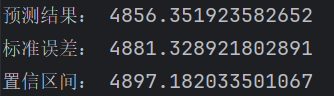
画出预测图代码如下:

获取置信区间,并画到图上代码:
# 获取预测值及其置信区间
forecast_result = model_fit.get_forecast(steps=5)
forecast_values = forecast_result.predicted_mean
forecast_conf_int = forecast_result.conf_int()
# 绘制置信区间
plt.fill_between(forecast_values.index, forecast_conf_int.iloc[:, 0], forecast_conf_int.iloc[:, 1], color='pink', alpha=0.5, label='Confidence Interval')
# 绘制拟合曲线和预测数据
plt.plot(data[u'销量'], label="模型数据")
plt.plot(forecast_values, label="预测数据")
plt.legend()
plt.show()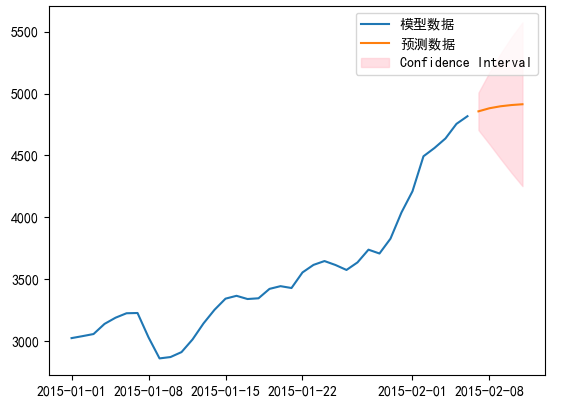
完整代码如下所示:
import pandas as pd
#参数初始化
discfile ='D:/daily/data1/arima_data.xls'
forecastnum = 5
data = pd.read_excel(discfile, index_col = u'日期')
#时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
data.plot()
plt.show()
#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为:', ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plt.show()
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() #偏自相关图
print(u'差分序列的ADF检验结果为:', ADF(D_data[u'销量差分'])) #平稳性检测
#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为:', acorr_ljungbox(D_data, lags=1)) #返回统计量和p值
import pandas as pd
import numpy as np
from statsmodels.tsa.arima.model import ARIMA
import warnings
warnings.filterwarnings("ignore")
data[u'销量'] = data[u'销量'].astype('float64')
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try:
model = ARIMA(data, order=(p, 1, q)).fit()
bic = model.bic
tmp.append(bic)
except:
tmp.append(float('inf')) # 将失败的值替换为无穷大
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix) #将bic矩阵转换为DataFrame
# 找出最小值位置
min_idx = np.unravel_index(np.nanargmin(bic_matrix.values), bic_matrix.shape)
p, q = min_idx
print(u'BIC最小的p值和q值为:%s、%s' %(p, q))
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt
# 拟合 ARIMA 模型
model = ARIMA(data, order=(p, 1, q))
model_fit = model.fit()
# 获取预测值及其置信区间
forecast_result = model_fit.get_forecast(steps=5)
forecast_values = forecast_result.predicted_mean
forecast_conf_int = forecast_result.conf_int()
# 绘制拟合曲线和预测数据
plt.plot(data[u'销量'], label="模型数据")
plt.plot(forecast_values, label="预测数据")
# 绘制置信区间
plt.fill_between(forecast_values.index, forecast_conf_int.iloc[:, 0], forecast_conf_int.iloc[:, 1], color='pink', alpha=0.5, label='Confidence Interval')
plt.legend()
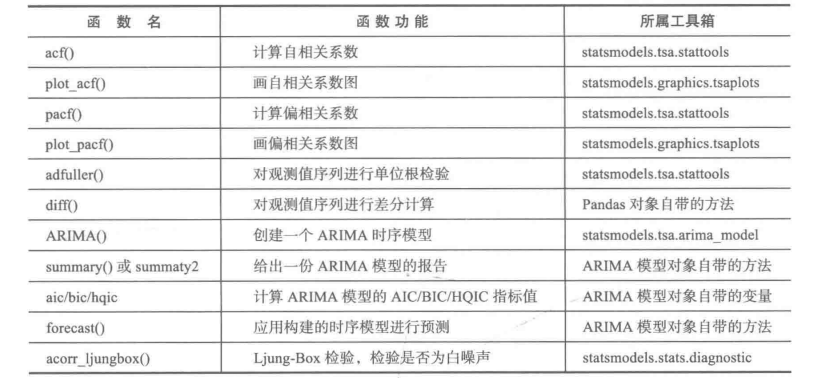
plt.show()附表:python时间序列函数功能及介绍