强化学习的数学原理是由西湖大学赵世钰老师带来的关于RL理论方面的详细课程,本课程深入浅出地介绍了RL的基础原理,前置技能只需要基础的编程能力、概率论以及一部分的高等数学,你听完之后会在大脑里面清晰的勾勒出RL公式推导链条中的每一个部分。赵老师明确知道RL创新研究的理论门槛在哪,也知道视频前的你我距离这个门槛还有多远。
本笔记将会用于记录我学习中的理解,会结合赵老师的视频截图,以及PDF文档Book-Mathematical-Foundation-of-Reinforcement-Learning进行笔记注释,之后也会补充课程相关的代码样例,帮助大家理解
笔记合集链接(排版更好哦🧐):《RL的数学原理》
记得点赞哟(๑ゝω╹๑)
Action
Agent在每个状态能够采取的行动
ActionSpace是依赖于State的,即不同状态会对应不同的ActionSpace

State transition
当采取一个action,Agent从一个State,转移到另一个State的过程


我们设计允许Agent踏入禁止区域,再惩罚扣分,而不是禁止进入,一是避免状态空间被缩小,而是适当的尝试扣分项,可能能创造更高的奖励。
状态转移矩阵
State transition可以用一个状态转移矩阵表示,这样表示相当直观,但是只能表示确认性的情况,因此现实中使用较为受限

状态转移可能性
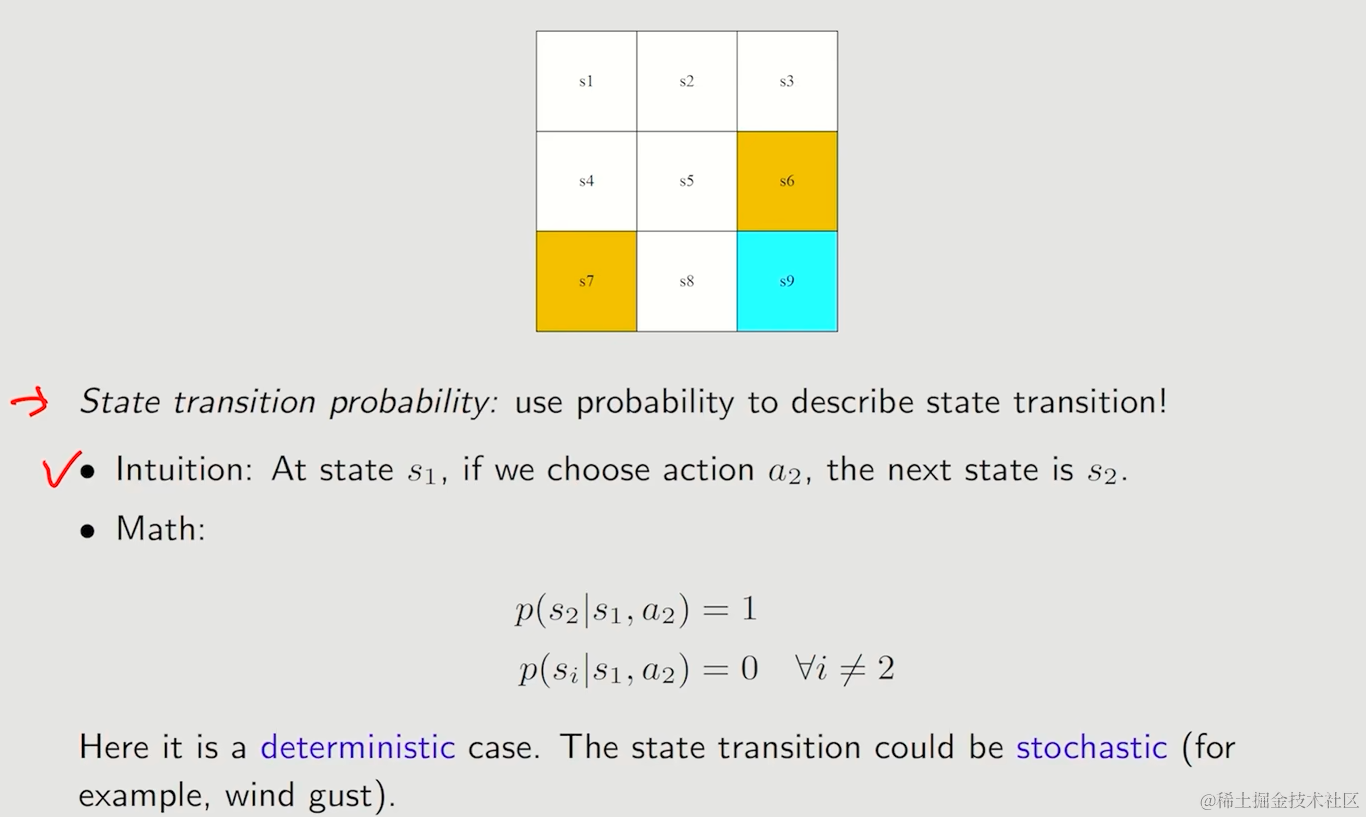
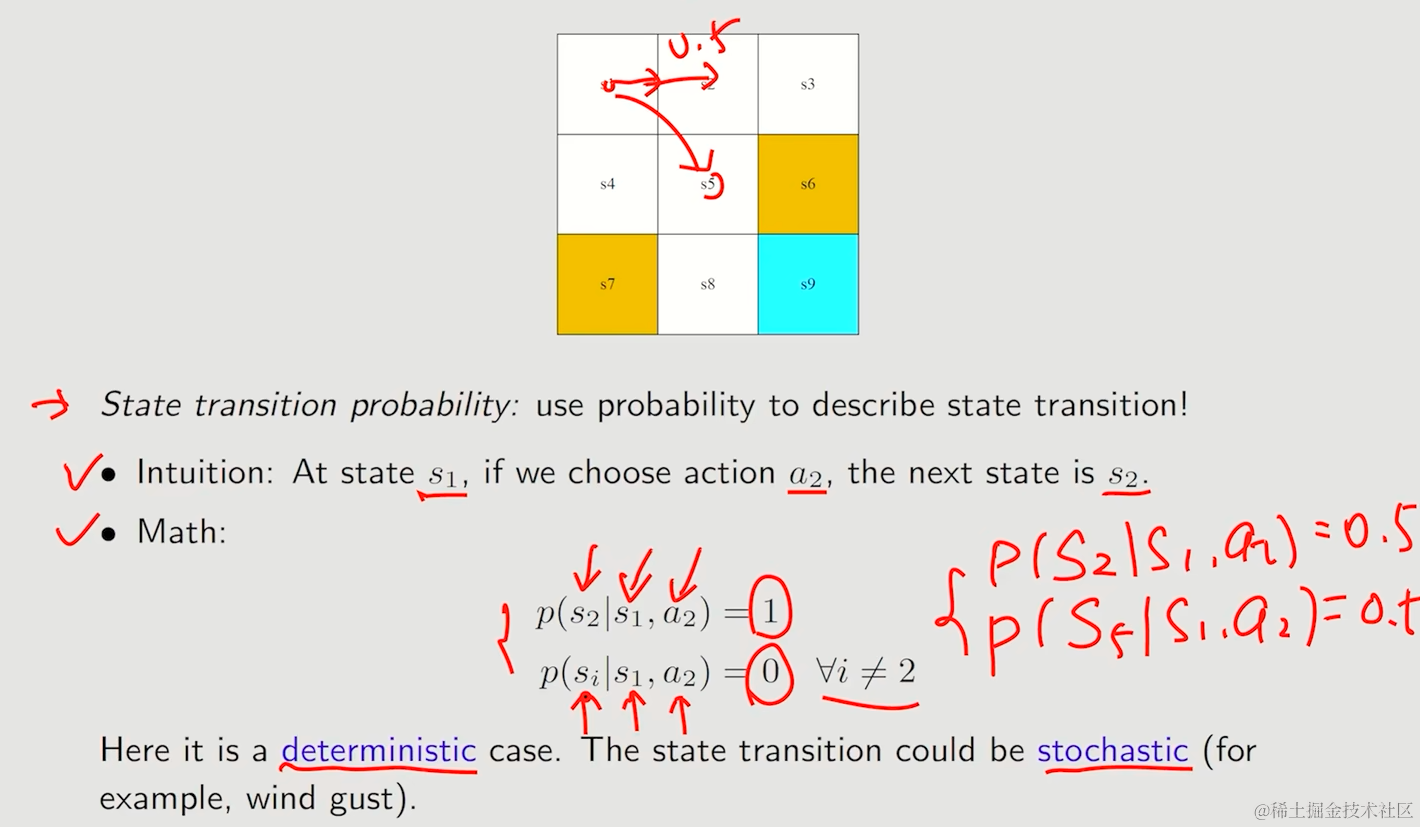
用条件概率来表达这种有随机性的例子,让状态转移的概率形式更加一般化
Policy
Agent被告知在一个状态会采取的动作,给予这个Policy,能够创建一条路径
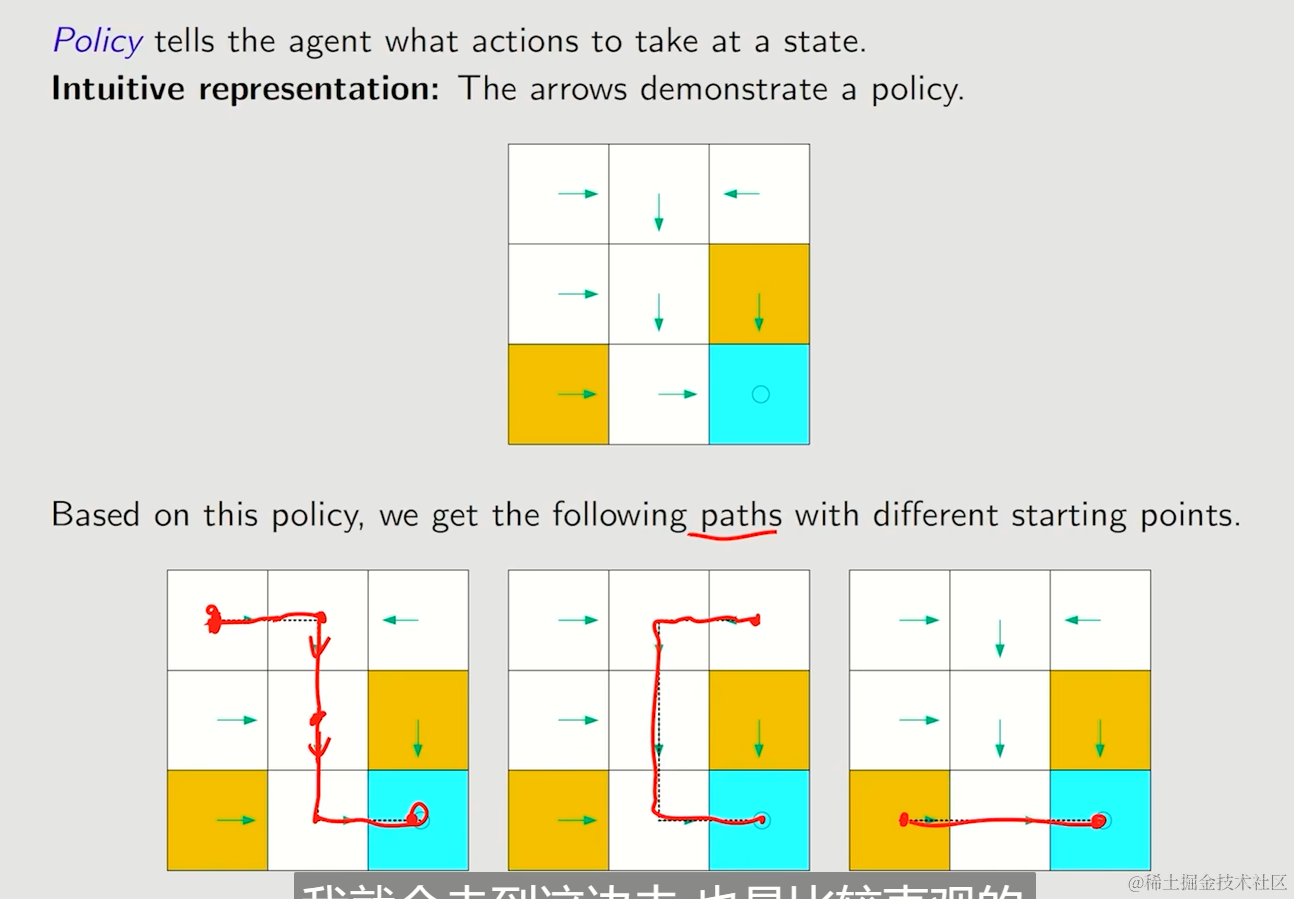
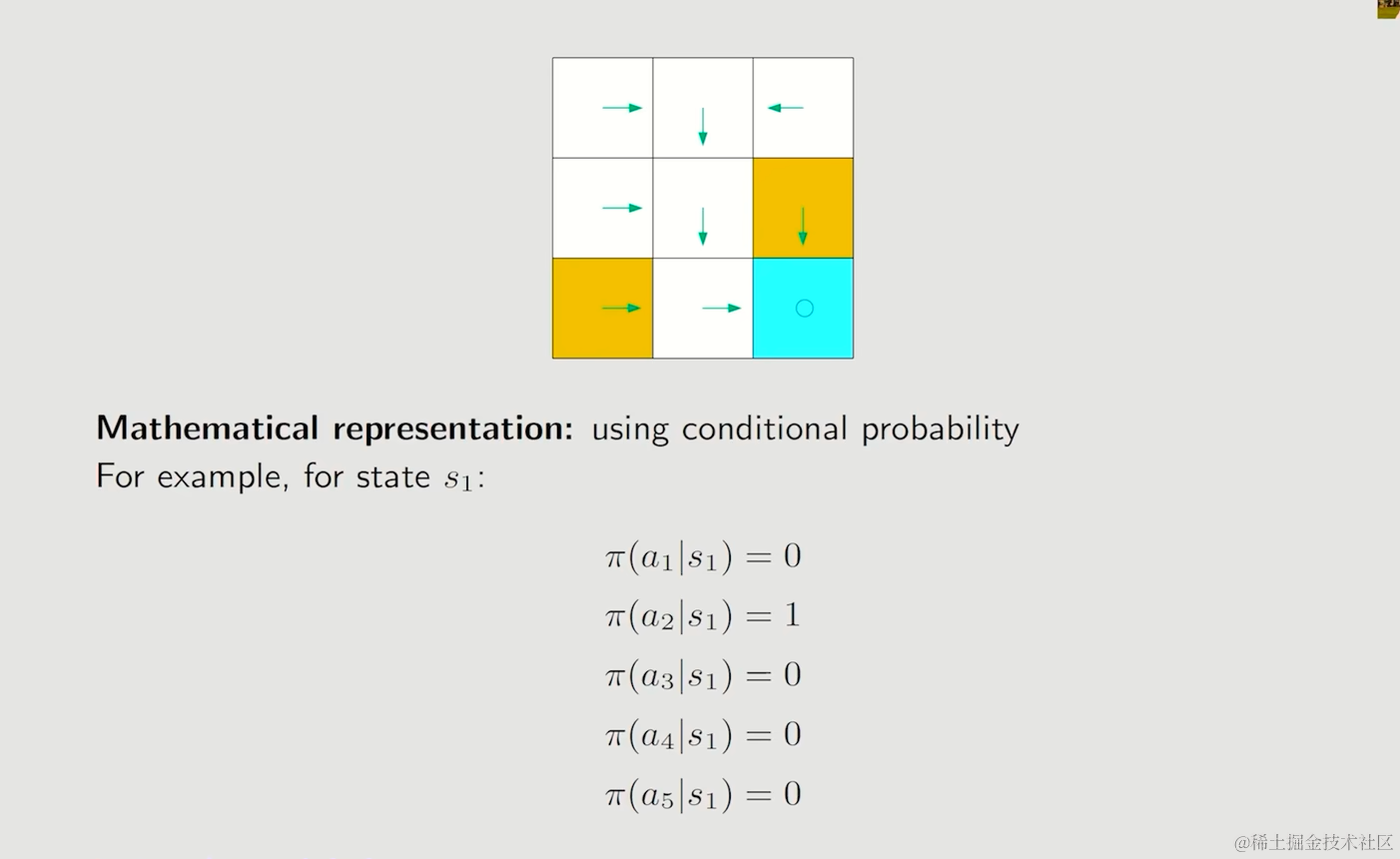
我们仍然使用条件概率来表示策略,使用符号π来表示任何一个state下,一个action的条件概率是多少
Reward
Agent在采取了一个动作后获得的一个实数标量
- 正数即鼓励行为的发生
- 负数即不被希望发生的行为
- 0一般没有意义,但是相对来说算是奖励
Reward是我们和机器交互的一种方式,去引导Agent实现合适的策略

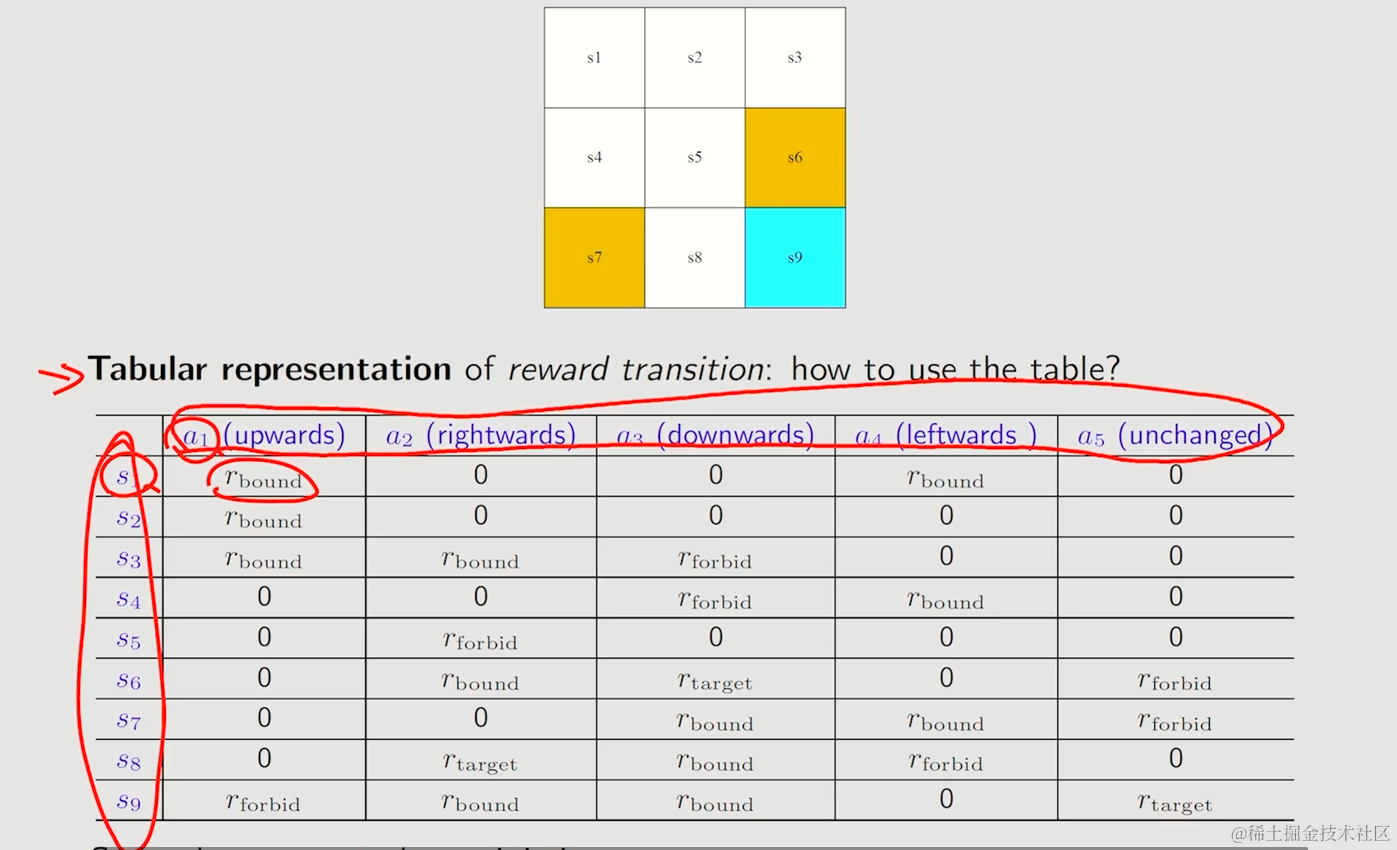
小贴示
- 当reward的产生存在概率时,则表格不再适用
- 只要你努力学习你就应该得到奖励,但具体数值并不会确定,同样的,Agent的奖励应该基于当前状态和奖励,而不是下一个状态
Trajectory and return
A state-action-reward chain

Return
对Trajectory的奖励进行求和
通过return,可以直观描述以及评估一个policy的好坏

Discounted return
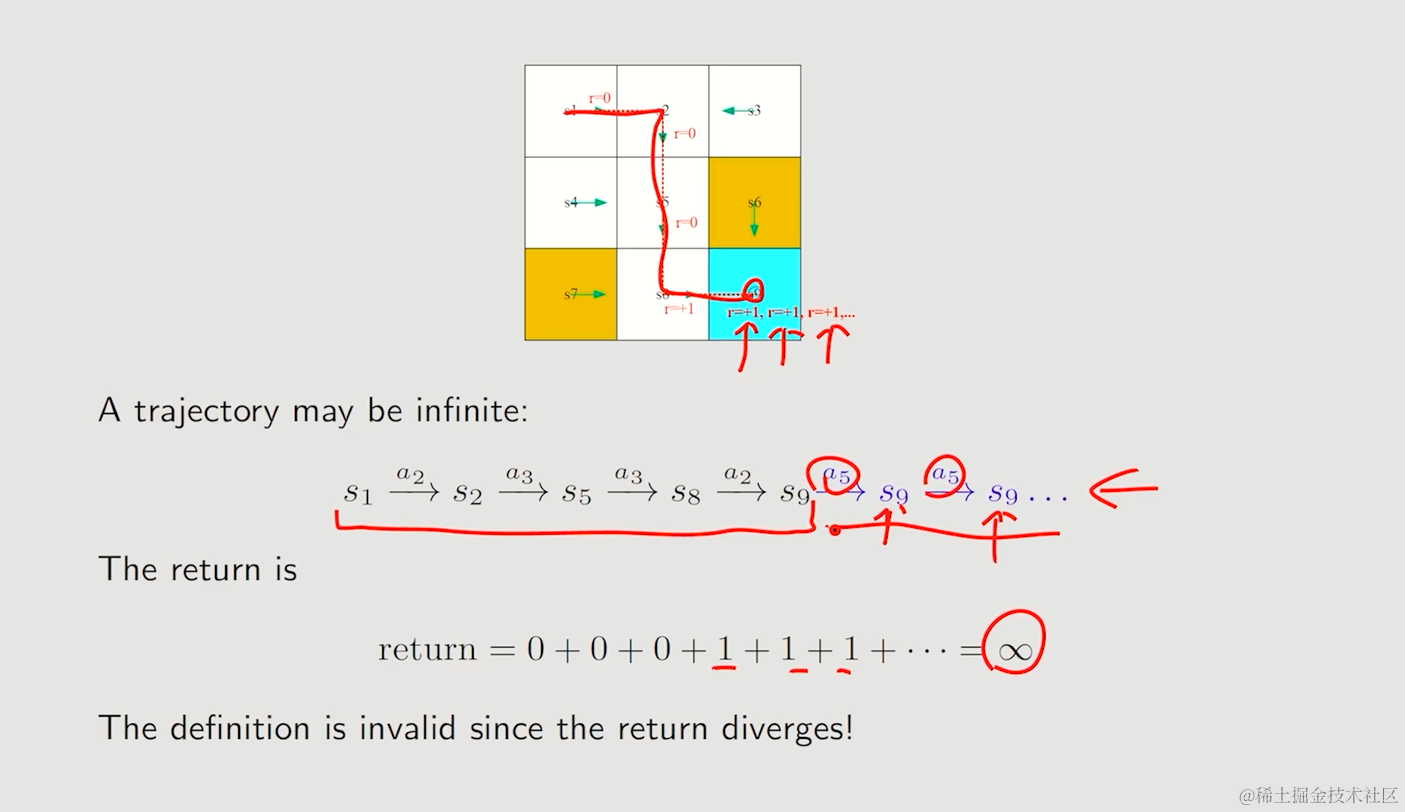

引入discount rate,避免return的发散,实现无穷级数的收敛
在return前添加折扣discount rate -> γ
- If γ is close to 0:让Agent的决策更趋向于即时奖励
- If γ is close to 1:让Agent的决策更趋向于长期奖励
Episode

episode可以理解为有terminal states(终止点)的trajectory,因此通常是有限步的,这样的任务被称为episodic tasks。
与之相对的是continuing tasks,与环境的交互不会终止

episodic tasks与continuing tasks的相互转化
- 将target状态设为absorbing state(可以理解为黑洞状态),一旦到达就无法离开
- 保持target为正常节点,使用奖励策略来阻止agent离开,允许agent跳出
我们采用第二种,虽然需要更多时间探索,但是最终的效果也将更加一般化
Markov decision process(MDP)[马尔科夫决策过程框架]

Key elements of MDP:
- Sets:
-
- State:the set of states S
- Action:the set of actions A(s) is associated for state s ∈ S.
- Reward:the set of rewards R(s,a).
- Probability distribution:
-
- State transition probability: at state s, taking action a, the probability to transit to state s’ is p(s’|s,a)
- Reward probability: at state s, taking action a,the probability to get reward r is p(r|s,a)
- Policy: at state s, the probability to choose action a is π(a|s)
- Markov property:memoryless property
p(st+1|at+1,st,…,a1,s0)=p(st+1|at+1,st),
p(rt+1|at+1,st,…,a1,s0)=p(rt+1|at+1,st).
All the concepts introduced in this lecture can be put in the framework in MDP.

之前的GWE可以被抽象为一个马尔科夫过程(Markov porcess)
Markov decision process becomes Markov process once the policy is given!
马尔科夫决策过程当有了一个明确的决策方式,就变成了马尔科夫过程
小结

By using grid-world examples, we demonstrated the following key concepts:
- State
- Action
- State transition, state transition probability p(s’|s,a)
- Reward, reward probability p(r|s,a)
- Trajectory, episode, return, discounted return
- Markov decision process







![[linux网络编程]UDP协议和TCP协议的使用](https://img-blog.csdnimg.cn/direct/3570e8b110374bacbde0e04828dd6848.png)