目录
摘要
ABSTRACT
1 FCN
2 双线性插值
3 膨胀卷积
3.1 gridding effect
摘要
本周继续学习了语义分割的内容,主要包括 FCN(全卷积网络)、双线性插值和膨胀卷积等方面。FCN 通过上采样的倍率可以划分为 FCN-32S、FCN-16S、FCN-8S,它们从不同程度上利用了下采样的信息。双线性插值是一种常用的图像处理技术,经常用于上采样操作,将特征图从低分辨率插值到高分辨率。膨胀卷积通过在卷积核的内部引入一个可调参数,膨胀率(Dilation Rate),来扩展卷积核的感受野,以此捕获更广泛的上下文信息,而无需增加参数或降低分辨率,但膨胀卷积也会导致“gridding effect”(格点效应),需要注意选择合适的膨胀率和层级组合,避免这种效应对模型性能的影响。本周我也学习了一种设计膨胀率的标准方法 HDC,用于避免gridding effect。
ABSTRACT
This week, We continued learning about semantic segmentation, focusing mainly on FCN (Fully Convolutional Network), bilinear interpolation, and dilated convolution. FCN can be categorized into FCN-32S, FCN-16S, and FCN-8S based on the upsampling factor, each utilizing the downsampling information to varying degrees. Bilinear interpolation is a common image processing technique often used for upsampling, interpolating feature maps from low to high resolution. Dilated convolution expands the receptive field of convolutional kernels by introducing a tunable parameter, the dilation rate, enabling the capture of broader contextual information without increasing parameters or reducing resolution. However, dilated convolution may lead to the "gridding effect," necessitating careful selection of dilation rates and layer combinations to mitigate its impact on model performance. We also learned a standard method called HDC for designing dilation rates to avoid the gridding effect.
1 FCN
FCN 首先通过一个预先训练好的卷积神经网络(如VGG、ResNet等)进行特征提取。这些网络通常经过在大规模图像数据集上进行了预训练,学习到了丰富的图像特征。最后的全连接层(FC)被去除,这样网络输出的特征图大小不再受输入图像大小限制,使得网络能够处理任意大小的图像。
在传统的卷积神经网络中,通常使用最后的全连接层来输出一个固定大小的特征向量,但是在 FCN 中,为了使输出能够适应输入图像的大小,使用了上采样技术。通常使用上采样技术为转置卷积(transposed convolution)或者双线性插值(bilinear interpolation),将低分辨率的特征图恢复到原始输入图像的分辨率大小,不同的上采样倍率也划分了不同类型的 FCN。
通过将不同层级的特征图进行融合,生成最终的语义分割结果。这种融合可以通过简单的连接或者更复杂的方法(如 skip connections)来实现。最后,对每个像素进行分类,以确定其所属的类别。这个阶段的实现取决于具体的任务,可以使用 softmax 或 sigmoid 激活函数来获得每个像素点属于各个类别的概率。
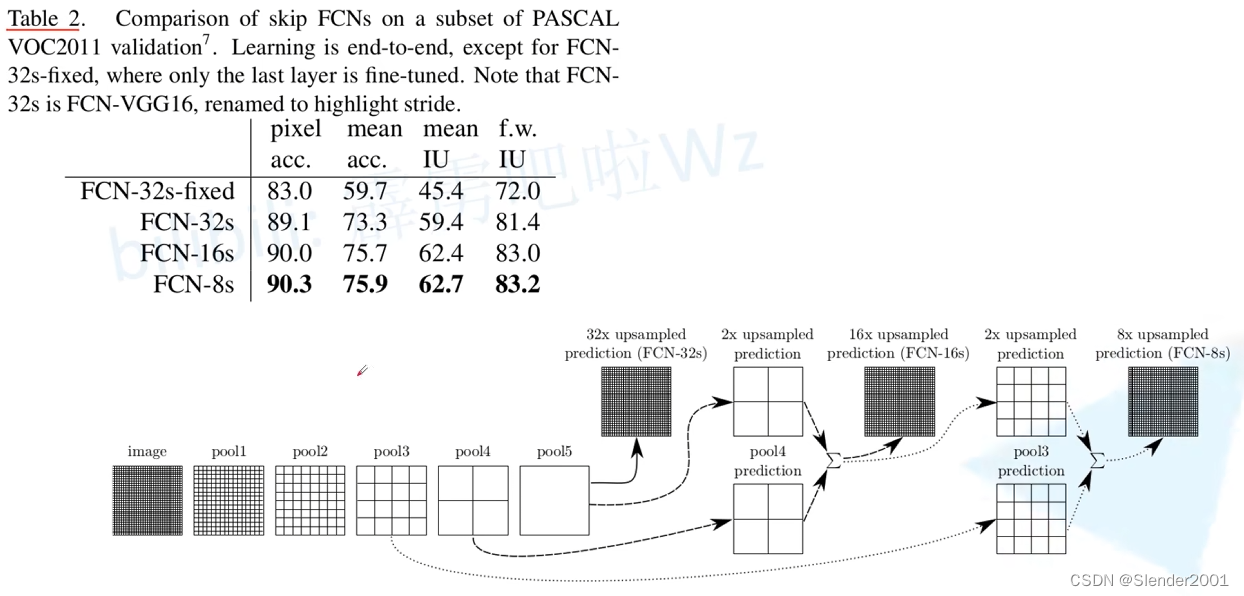
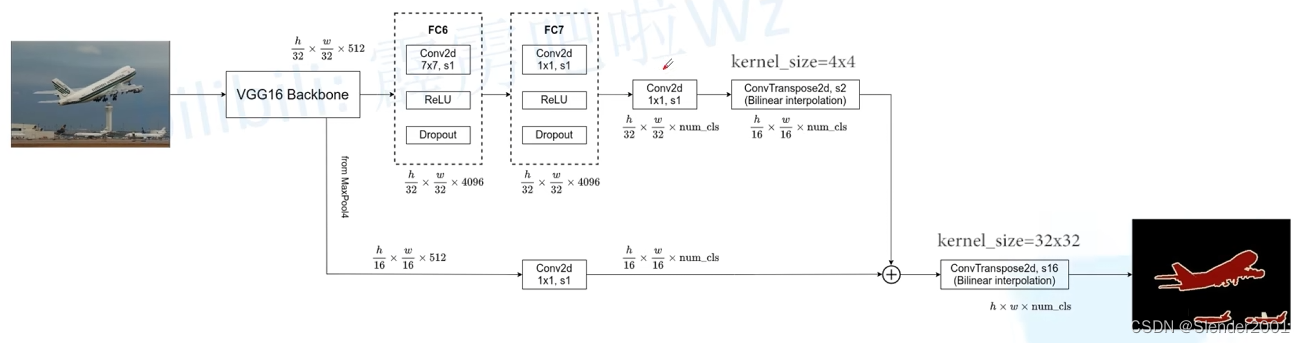
FCN-32S 是最简单的 FCN 变体。在此变体中,特征图由网络的最后一层直接上采样生成,因此上采样的倍率是 32 倍。通常会在 FC6 层增加卷积的 padding=3 以输出和 VGG16 Backbone 相同尺寸的特征图。注意,在 FC6、FC7 处理后,会使用一个卷积层将输出特征图的维度转为分类个数。FCN-32S 的上采样一般只采用双线性插值(冻结转置卷积的参数,减少计算量),因为在该倍率下转置卷积的效果不明显。

FCN-16S 在 FCN-32S 的基础上增加了一步跳跃连接(skip connection),以提高语义分割的精度。这个变体中,下采样 pool4 的 1/16 的特征图被加入到上采样后的特征图中,以提供更多的细节信息。
FCN-8S 是在 FCN-16S 的基础上再次增加了一步跳跃连接,这次是下采样 pool3 的 1/8 的特征图被加入到上采样后的特征图中。
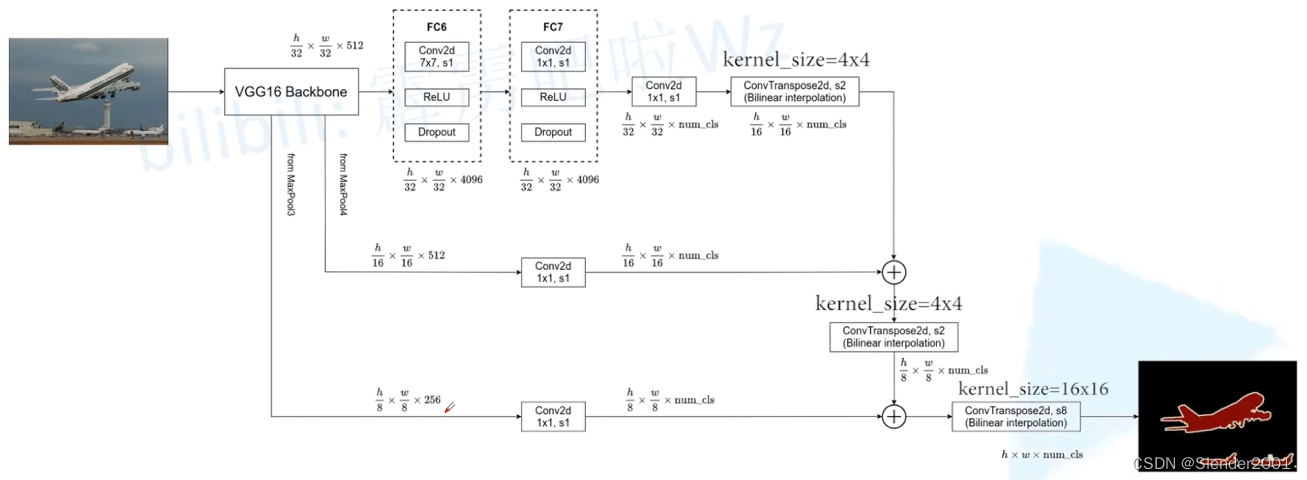
最后使用交叉熵损失函数计算 loss 以更新模型参数。

2 双线性插值
双线性插值是一种常用的图像处理技术,用于在离散网格上对图像进行平滑且连续的放大或缩小。在深度学习中,特别是在全卷积网络(FCN)等模型中,双线性插值经常用于上采样操作,以将特征图从低分辨率插值到高分辨率。插值是指根据已知数据点的数值,在其之间估算其他点的值的一种方法。双线性插值是插值方法的一种,用于在给定四个邻近的网格点的值的情况下估算两个坐标轴上任意点的值。用一个简单的例子来描述双线性插值进行上采样操作的过程。
假设有一张 3x3 大小的图片,其中的每个像素单位长为1,像素中心用红点表示。要将其放大到 5x5 大小,并确定每一个像素的值(蓝点)。首先,需要将这个 5x5 大小的图片与 3x3 大小的图片进行对齐。对齐的方法有两种,一种是角对齐,另一种是边对齐,具体展示如下:
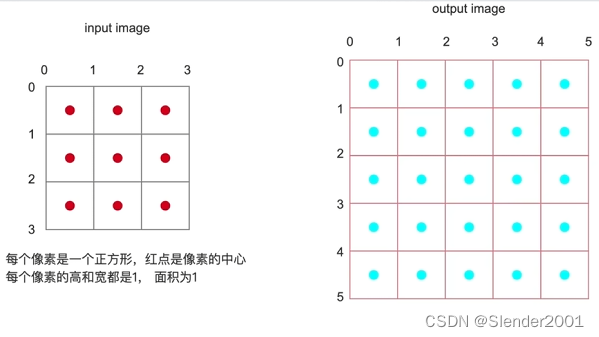


无论采用哪种对齐方式,第二步都是找出距离每一个目标像素(蓝点)最近的四个原图像素(红点),然后通过目标像素与原图像素的相对位置计算目标像素的值。放大一个目标像素来作为例子解释计算过程,观察可知,距离蓝点最近的四个红点分别为 v1、v2、v3 和 v4。红点间的距离为1,所以蓝点距离四条边的值可以定义为 a、1-a、b 和 1-b。至此可以先计算出蓝点在水平方向上的两个插值 p1 和 p2,计算公式为 p1=(1-b)*v1+b*v2,p2=(1-b)*v3+b*v4。注意,距离越近,权重越大,即与更大的距离相乘。最后,在垂直方向上进行插值即得到目标像素的值 p=(1-a)*p1+a*p2。
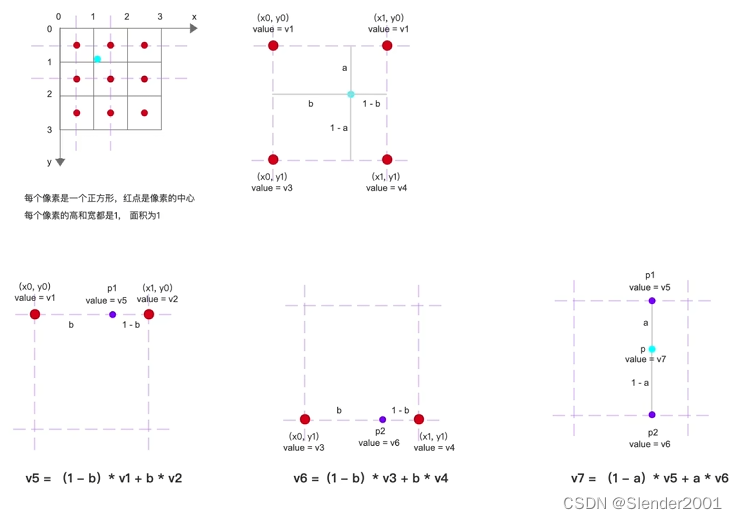
双线性插值代码:
def bilinear_interpolation(image, out_height, out_width, corner_align=False):
# 获取输入图像
height, width = image.shape[:2]
# 创建输出图像
output_image = np.zeros((out_height, out_width), dtype=np.float32)
# 计算 x、y 轴缩放因子
scale_x_corner = float(width - 1) / (out_width - 1) # (3-1)/(5-1)=0.5
scale_y_corner = float(height - 1) / (out_height - 1) # (3-1)/(5-1)=0.5
scale_x = float(width) / out_width # 3 / 5 = 0.6
scale_y = float(height) / out_height # 3 / 5 = 0.6
# 遍历输出图像的每个像素,分别计算其在输入图像中最近的四个像素的坐标,然后按照加权值计算当前像素的像素值
for out_y in range(out_height):
for out_x in range(out_width):
if corner_align:
# 计算当前像素在输入图像中的位置
x = out_x * scale_x_corner # 1 * 0.5 = 0.5
y = out_y * scale_y_corner # 1 * 0.5 = 0.5
else:
x = (out_x + 0.5) * scale_x - 0.5 # 1 * 0.5 = -0.2
y = (out_y + 0.5) * scale_y - 0.5 # 1 * 0.5 = -0.2
x = np.clip(x, 0, width - 1) # 0
y = np.clip(y, 0, height - 1) # 0
# 计算当前像素在输入图像中最近的四个像素的坐标
x0, y0 = int(x), int(y)
x1, y1 = x0 + 1, y0 + 1
# 对原图像边缘进行特殊处理
if x0 == width - 1:
x0 = width - 2
x1 = width - 1
if y0 == height - 1:
x0 = height - 2
x1 = height - 1
xd = x - x0
yd = y - y0
p00 = image[y0, x0]
p01 = image[y0, x1]
p10 = image[y1, x0]
p11 = image[y1, x1]
x0y = p01 * xd + (1 - xd) * p00
x1y = p11 * xd + (1 - xd) * p10
output_image[out_y, out_x] = x1y * yd + (1 - yd) * x0y
return output_image3 膨胀卷积
膨胀卷积(Dilated Convolution),也称为空洞卷积(Atrous Convolution),是卷积神经网络(CNN)中常用的一种卷积操作。相比于传统的卷积操作,膨胀卷积在保持特征图尺寸的同时增加了感受野的大小。这种技术被广泛应用于各种计算机视觉任务中,如语义分割、图像超分辨率、视频分析等。
在传统的卷积操作中,我们以固定的卷积核大小(通常是 3x3 或 5x5)在输入特征图上滑动,从而生成输出特征图。例如,一个 3x3 的卷积核应用到一个特征图上如下所示:
输入特征图:
| 1 2 3 4 5 |
| 6 7 8 9 10|
| 11 12 13 14 15|
| 16 17 18 19 20|
| 21 22 23 24 25|
卷积核:
| a b c |
| d e f |
| g h i |
输出特征图:
| p1 p2 p3 |
| p4 p5 p6 |
| p7 p8 p9 |
在这个示例中,步长为1,输出特征图中的每个位置(例如,p1, p2, p3, …)都是通过卷积核与对应输入图像的区域进行点乘并求和得到的。这个区域的大小由卷积核的大小确定。
膨胀卷积通过在卷积核的内部引入一个可调参数,通常称为膨胀率(Dilation Rate),来扩展卷积核的感受野。膨胀率决定了在卷积核中插入的零值的间距。在每个方向上,膨胀率值决定了在卷积核中取样点之间的空白距离。
输入特征图:
| 1 2 3 4 5 |
| 6 7 8 9 10|
| 11 12 13 14 15|
| 16 17 18 19 20|
| 21 22 23 24 25|
填充特征图(padding为2):
| 0 0 0 0 0 0 0 0 0 |
| 0 0 0 0 0 0 0 0 0 |
| 0 0 1 2 3 4 5 0 0 |
| 0 0 6 7 8 9 10 0 0 |
| 0 0 11 12 13 14 15 0 0 |
| 0 0 16 17 18 19 20 0 0 |
| 0 0 21 22 23 24 25 0 0 |
| 0 0 0 0 0 0 0 0 0 |
| 0 0 0 0 0 0 0 0 0 |
膨胀卷积核(膨胀率为2):
| a 0 b 0 c |
| 0 0 0 0 0 |
| d 0 e 0 f |
| 0 0 0 0 0 |
| g 0 h 0 i |
输出特征图:
| p1 p2 p3 p4 p5 p6 |
| p7 p8 p9 p10 p11 p12 |
| p13 p14 p15 p16 p17 p18 |
| p19 p20 p21 p22 p23 p24 |
| p25 p26 p27 p28 p29 p30 |
在这个示例中,膨胀率为2,步长为1,因此在水平和垂直方向上插入了一个间隔。这意味着卷积核的感受野变大了,但输出特征图的尺寸却保持不变。输出特征图中的每个位置仍然是通过卷积核与对应输入图像的区域进行点乘并求和得到的。
膨胀率决定了卷积核内部的采样间隔。具体来说,膨胀率为 r 的卷积核的感受野大小为 (2r + 1) x (2r + 1)。因此,通过增加膨胀率,我们可以有效地增加卷积核的感受野,从而捕获更广阔范围内的上下文信息,而无需增加参数或降低分辨率。
膨胀卷积的优点:
① 更大的感受野:膨胀卷积可以通过增加膨胀率来实现更大的感受野,以捕获更广泛的上下文信息。
② 保持特征图尺寸:与传统卷积相比,膨胀卷积可以在不降低分辨率的情况下增加感受野大小。
3.1 gridding effect
在使用膨胀卷积时,一个常见的问题是“gridding effect”(格点效应)。这种效应发生的原因是膨胀卷积的间隔性导致输入图像的某些区域被重复采样,而相邻区域则可能完全被忽略,从而在输出特征图中形成了类似网格的模式。这种间断性的采样结果导致模型在空间连续性上表现不佳,尤其是在处理需要高空间一致性的任务时,如图像分割。
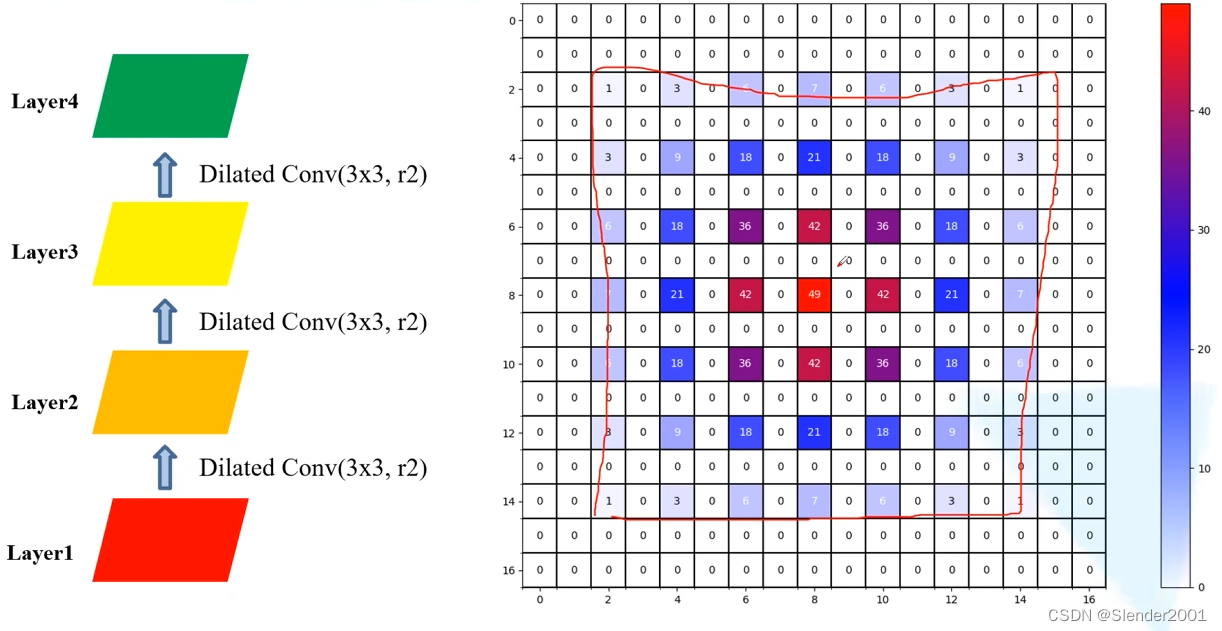
上图中的每一个卷积层都使用了相同的膨胀率 r=2,感受野的范围虽然够大(13x13),但是其中存在相当一部分数据完全没有被用于计算,即产生了 gridding effect 现象。如果按 r=1,r=2,r=3,递增的膨胀率进行卷积,则结果如下,在感受野的范围同样为 13x13 的基础上运用到了每一个数据进行计算,很明显对 gridding effect 现象有一定的抑制作用。
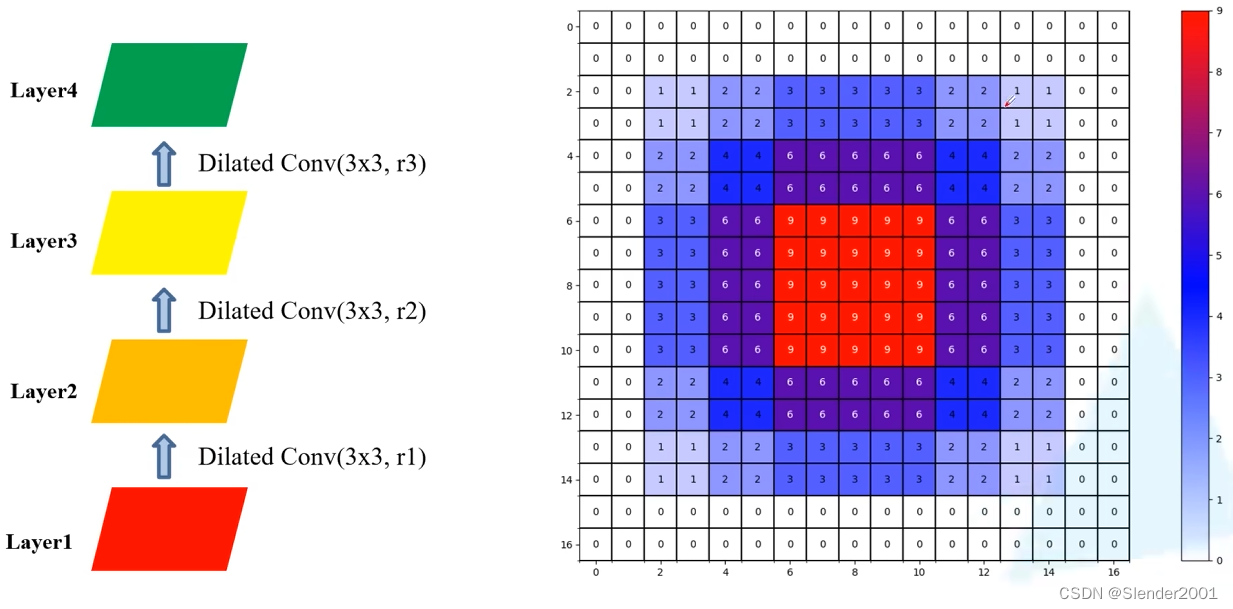
由此可见,不同层的膨胀率选择非常重要。通过实验,对于不同层的膨胀率选择通常基于如下标准:

所以,当 kernel size = 3 时,三层卷积的膨胀率应该为 [1,2,5],而非 [1,2,9],用具体的实验结果也能证明这一点:
[1,2,5]的感受野情况:

[1,2,9]的感受野情况:

此外,标准中还建议,所选膨胀率的公约数最好为1,否则同样会存在 gridding effect,例如 [2,4,8],公约数为2,感受野情况如下所示。而且当卷积层大于3层时,最好采用“锯齿状”的膨胀率,例如 [1,2,5,1,2,5]。



上述的标准也称为 HDC。