Kuramoto模型源远流长，这里不会对它做过于理论方面的讲解，只是面向动力学重构的工作中，可能要用到Kuramoto模型的相关介绍。

假设读者了解的常微分方程基本概念，图论知识，了解邻接矩阵，

通过本文，你将获得

1. 单个节点的Kuramoto模型，以及其中参数的含义

2. 正弦耦合的Kuramoto

3. Kuramoto模型的平均场分析 (Mean-Field)，这也揭示了模型与复分析的关系

4. 一般的Kuramoto网络

Kuramoto网络模型

数学表达

单个节点

参考[1]，我们考虑单个节点的Kuramoto模型

$$\frac{d\theta }{dt}=\omega \text{\hspace{1em}(1)}$$

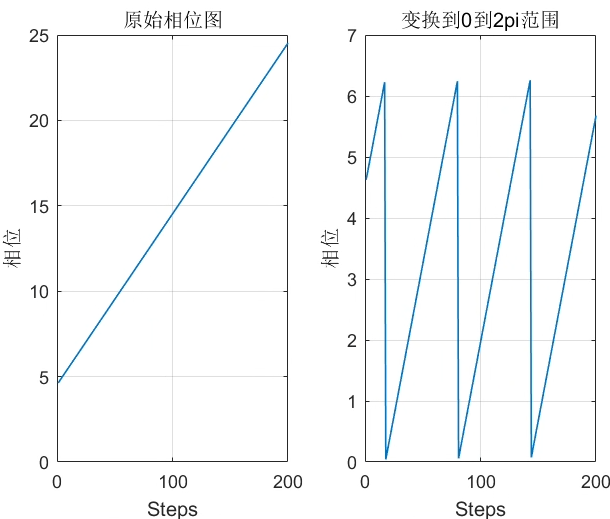
明显这是一个线性常微分方程模型，它的解为$\theta (t)=\omega t+\theta (0)$，不难想象，当自然频率$\omega$更大，$\theta$的斜率也会变化得越陡，如图1.a所示；绿色的${\omega }_3$参数更高，蓝色的${\omega }_1$更小

既然是振子模型，我们认为 $\theta +2\pi$ 与 $\theta$ 没有区别，于是我们可以用对 $2\pi$ 取mod的方式，得到图1.b的齿状周期震荡图；

图1

既然 $\theta$ 的变化范围从0到$2\pi$，从这个角度，我们可以从单位圆的角度看待振子。同样，自然频率最大的绿色振子走在了最前面。

图2

正弦耦合

Kuramoto网络模型可以用如下的方式耦合在一起，也被称为正弦耦合(Sinusoidal Coupling)[YTB]：

$$\begin{array}{r}\frac{d{\theta }_i}{dt}={\omega }_i+\frac{K}{N}{\sum }_{j=1}^N\sin \left({\theta }_j-{\theta }_i\right)i=1\dots N\end{array}\text{\hspace{1em}(2)}$$

这时是全连接网络，不过可以看出一些有趣的性质。
如果 $0<{\theta }_j-{\theta }_i<\pi$，那么 $\sin \left({\theta }_j-{\theta }_i\right)>0$。在2个节点的情况下，$j$号振子的 ${\theta }_k$会有变大趋势，而 $i$ 号振子相位有变小的趋势。（相比与他们各自的自然频率而言）

---

大家也能想象，当 $0<{\theta }_j-{\theta }_i<\pi$的时候，会发生怎样的运动🤔

一些情况，会发生锁频(Frequency Locking)，即：两个振子一开始会拉开距离，然后保持在一个特定的距离前行。关于锁频的详细讲解就先不说了。其实用相位差 $\varphi ={\theta }_1-{\theta }_1$ 去做分析就行。

另一种情况是，当 ${\omega }_1={\omega }_2=...={\omega }_N$，且$K>0$时，这些振子会逐渐从散乱的状态收敛到完全同步的状态。这种情况可以类似的用减法来分析，比如构造向量 ${\hat{\theta }}_i(t)={\theta }_i-\omega t$。

$$\begin{array}{rl}& {\hat{\theta }}_i(t)={\theta }_i-\omega t\\ & \frac{d{\hat{\theta }}_i}{dt}=\frac{K}{N}\sum _{j=1}^N\sin \left({\hat{\theta }}_j-{\hat{\theta }}_i\right)\end{array}\text{\hspace{1em}(3)}$$

可以看到， ${\hat{\theta }}_i$ 的个稳定点是所有${\hat{\theta }}_i$都为0的情况。

平均场分析 (Mean-Field)

单纯出于好奇了解Kuramoto与复数的联系，但这块在后续并不会用到

根据一个复分析欧拉公式：$\begin{array}{rl}& e^{\mathbf{i}\theta }=\cos (\theta )+\mathbf{i}\sin (\theta )\\ & \text{Im}\left(e^{\mathbf{i}\theta }\right)=\sin (\theta )\end{array}$，公式(3)可表为：

KaTeX parse error: \tag works only in display equations

接下来是一个不那么容易理解的设定，为了进一步对上面的公式进行处理，我们定义一个叫做 Kumamoto Order Parameter 的东西，就是令：$\frac{1}{N}{\sum }_{j=1}^N{e}^{\mathrm{i}{\hat{\theta }}_j}:=r{e}^{(\mathrm{i}\hat{\varphi })}$。（毕竟复数加复数还是一个复数，现在只是用 $r$ 和 $\hat{\varphi }$来进行刻画）。从而，公式(4)可以进一步化简为

$\frac{d{\hat{\theta }}_i}{dt}=\text{Im}\left(rK{e}^{-i{\hat{\theta }}_i}{e}^{\mathbf{i}\hat{\varphi }}\right)=\text{Im}\left(rK{e}^{(\mathrm{i}\left(\hat{\varphi }-{\hat{\theta }}_i\right)}\right)=rK\sin \left(\hat{\varphi }-{\hat{\theta }}_i\right)$

从而，同步的速度由 $r$ 和 $\varphi$ 来决定，他们看起来代表了网络的某种全局性质。

一般网络

上面都是在谈论全连接网络，这里我们给不同的 $i$ 和 $j$之间赋予不同的形式，[Yan,2023]

${\dot{\theta }}_i={\omega }_i+\frac{K}{N}{\sum }_{j=1}^N{a}_{ij}\sin \left({\theta }_j-{\theta }_i\right),(i=1,\cdots ,N),$

其中，${\theta }_i$表示第i个振子的相位，${\omega }_i$表示第i个振子的自然频率。$A=a_{ij}$为邻接矩阵，$a_{ij}=1$第i个节点会受到第j个节点的影响（j→i）。0表示没有连接。$\frac{K}{N}$表示整体的连接强度，当K很小时，所有振子都会倾向以他们的自然频率运动，当K比较大时，每个振子会受到自己邻居节点的影响。当K超级大时，所有的振子将会以一个共同的频率${\sum }_i{\omega }_i/N$运动。

仿真

首先，绘制单个Kuramoto的图形。因为是线性模型，每次将得到的相位保持在0到2pi的范围，如下图3所示

图3

接下来，我们进行2个节点的绘制，这里的主要困难在于连接矩阵和累乘的定义，在matlab中的编程可能会混淆，这里这里我们设$A=\left[\begin{array}{ll}{a}_{11}& a_{12}\\ a_{21}& a_{2n}\end{array}\right]$, theta是表示状态变量的列向量$\left[\begin{array}{l}{\theta }_1\\ {\theta }_2\end{array}\right]$，于是theta'-theta为$\left[\begin{array}{cc}0& {\theta }_2-{\theta }_1\\ {\theta }_1-{\theta }_2& 0\end{array}\right]$。

可以验证：$\left[\begin{array}{l}{\theta }_1\\ {\theta }_2\end{array}\right]=\left[\begin{array}{l}{\omega }_1+\frac{K}{N}\left(a_{11}\times 0+a_{12}\times \left({\theta }_2-{\theta }_1\right)\right)\\ {\omega }_2+\frac{K}{N}\left(a_{21}\times \left({\theta }_1-{\theta }_2\right)+a_{22}\times 0\right)\end{array}\right]dt+\left[\begin{array}{l}{\theta }_1\\ {\theta }_2\end{array}\right]$是与公式2一致的。

% 计算每个振荡器的相位变化率
dtheta = omega + (K/N) * sum(A .* sin(theta' - theta),2);

% 更新相位
theta = theta + dtheta * dt;

图4

图4：在16左右出现了两个峰，这是从15之后，被${\theta }_1-{\theta }_2$给往回拉扯导致的（可以对比黄线看出红线被拉扯的轨迹）

参考

[1] YTB Episode 1: Kuramoto Model Part 12

[2] 源码地址

[3] flowus博客