归并排序详解

归并排序的核心思想：

递归实现：

非递归实现：

时间复杂度：

空间复杂度：

应用场景：

本文全部以升序为例：

归并排序的核心思想：

先分解在合并：

1.归并的归，指的是回归到最小范围，也就是把要排序的数组，先分解成多个小的组合。

2.归并的并，就是，先把每个小的组合实现排序，然后把若干个有序的组合合并成一个有序的组合，从而实现排序。

如图，举一个简单的例子：

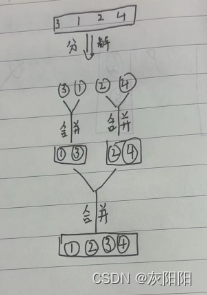这样就实现了升序

再举个例子：

把10,6,7,1,3,9,4,2排列成升序：

归并排序的一般步骤都是，先分解，在合并。而递归实现和非递归实现，合并的方式都是一样的，只是分解的方法有所差异

所以我们先来把合并的方法讲了先：

如何把两个两个的有序组合，合并成一个有序的组合？

还是举一个简单的例子来讲解：

arr1={1,3} 和arr2={2,4}

如何把这两个有序的数组合并成arr3={1,2,3,4}呢？

思路：

1、定义一个临时数组tmpArr，长度是上面两个小数组元素之和。

2、定义两个指针,c1和c2，分别指向arr1和arr2的首元素。

3、比较两个指针所指的元素，把小的那个元素先存放到临时数组中，然后指针往前移动，以此类推，直到arr1和arr2两个数组全部遍历完。

这时候，我们就得到了一个合并后的有序的临时数组tmpArr了。

具体代码及注释细节介绍：

private static void merge(int[] arr,int left,int right,int mid){
 
//arr是我们要排序的整个数组
//[left,right]是一个闭区间，且一定是arr数组中的有效下标
//mid是下标left和right的中间值
//需要合并的数组其实就是：
//[left,mid]以及[mid+1,right]---------》这两个数组都是有序的     

    }

    private static void mergeArr(int[] arr, int left, int right, int mid) {//受到deComposeArr的保护，所有的下标都是有效的

        /*
         * 对两个相邻区间的有序数组合并成一个有序的数组
         * [left,mid]和[mid+1,right]
         * 记住：这两个数组都是已经排好序的了啊啊啊啊啊啊啊啊，先不用问为什么，等看完，回过头来想，就自然懂了*/

        //第一个数组的两个首尾下标
        int head1 = left;
        int end1 = mid;

        //第二个数组的两个首尾下标
        int head2 = mid + 1;
        int end2 = right;//可以不用定义这么多下标，mid和right可以直接用，我这样写只是让大家好理解

        //定义一个临时数组，长度是   *上面两个数组长度之和*
        int[] tmpArr = new int[right - left + 1];//对，要加一，即使一个简单的数学问题

        int k = 0;//临时数组的下标

        while (head1 <= end1 && head2 <= end2) {//只要两个数组，没有全部放进临时数组，就一直循环

            //如果arr[head1]比较小，就把arr[head1]先放进临时数组
            if (arr[head1] < arr[head2]) {
                tmpArr[k++]=arr[head1++];//后置加加，存完，就去判断下一个位置的大小关系
            }else{//和if的逻辑一样
                tmpArr[k++]=arr[head2++];
            }
        }
        
/*
*         除了上面的while循环后，实际上还没有完全把tmpArr数组装完，因为
* 条件head1<=end1或者head2<=end2可能只有一个不符合条件，所以，要记得判断
 */        //把剩下的直接放到tmpArr数组即可
        while(head1<=end1){
            tmpArr[k++]=arr[head1++];
        }
        while(head2<=end2){
            tmpArr[k++]=arr[head2++];
        }
        

        for (int i = 0; i <k ; i++) {//实际上k，就是临时数组的长度
            arr[left+i]=tmpArr[i];
        }

    }

下面的递归和非递归都要用到mergeArr方法(合并)！

递归实现：

前文讲到不论是递归还是非递归，实际上不一样的就在，分解这个步骤，所以我们重点看看，如果把一个数组，分成若干个小的数组，然后去合并的。

有了上面的合并方法，其实递归就很好写了代码：

 private static void deComposeArr(int[] arr, int left, int right) {//先分解，在合并
            if(left>=left)return;//检测无效下标，就直接退出

            int mid=(left+right)/2;
        //递归分解两个区间，直到分成一个一个的元素，然后有序合并
        /*
         * 第一个：
         * 【left,mid】*/

        /*
         * 第二个：
         * 【mid+1,right】*/
            deComposeArr(arr,left,mid);
            deComposeArr(arr,mid+1,right);

            //分解合并后，在最后合并即可
            mergeArr(arr,left,right,mid);

    }

归并排序的递归写法_整体代码：

class TestMerge {
    public static void mergeSort(int[] arr) {//为了保持接口的一致性，只传递一个数组，所以定义这个方法去调用deCompose
        deComposeArr(arr,0,arr.length-1);
    }

    private static void deComposeArr(int[] arr, int left, int right) {//先分解，在合并
            if(left>=right)return;//检测无效下标，就直接退出

            int mid=(left+right)/2;
        //递归分解两个区间，直到分成一个一个的元素，然后有序合并
        /*
         * 第一个：
         * 【left,mid】*/

        /*
         * 第二个：
         * 【mid+1,right】*/
            deComposeArr(arr,left,mid);
            deComposeArr(arr,mid+1,right);

            //分解合并后，在最后合并即可
            mergeArr(arr,left,right,mid);

    }

        private static void mergeArr(int[] arr, int left, int right, int mid) {//受到deComposeArr的保护，所有的下标都是有效的

            /*
             * 对两个相邻区间的有序数组合并成一个有序的数组
             * [left,mid]和[mid+1,right]
             * 记住：这两个数组都是已经排好序的了啊啊啊啊啊啊啊啊，先不用问为什么，等看完，回过头来想，就自然懂了*/

            //第一个数组的两个首尾下标
            int head1 = left;
            int end1 = mid;

            //第二个数组的两个首尾下标
            int head2 = mid + 1;
            int end2 = right;//可以不用定义这么多下标，mid和right可以直接用，我这样写只是让大家好理解

            //定义一个临时数组，长度是   *上面两个数组长度之和*
            int[] tmpArr = new int[right - left + 1];//对，要加一，即使一个简单的数学问题

            int k = 0;//临时数组的下标

            while (head1 <= end1 && head2 <= end2) {//只要两个数组，没有全部放进临时数组，就一直循环

                //如果arr[head1]比较小，就把arr[head1]先放进临时数组
                if (arr[head1] < arr[head2]) {
                    tmpArr[k++]=arr[head1++];//后置加加，存完，就去判断下一个位置的大小关系
                }else{//和if的逻辑一样
                    tmpArr[k++]=arr[head2++];
                }
            }

    /*
    *         除了上面的while循环后，实际上还没有完全把tmpArr数组装完，因为
    * 条件head1<=end1或者head2<=end2可能只有一个不符合条件，所以，要记得判断
     */        //把剩下的直接放到tmpArr数组即可
            while(head1<=end1){
                tmpArr[k++]=arr[head1++];
            }
            while(head2<=end2){
                tmpArr[k++]=arr[head2++];
            }


            for (int i = 0; i <k ; i++) {//实际上k，就是临时数组的长度
                arr[left+i]=tmpArr[i];
            }

        }
}

非递归实现：

其实分解思路都一样，就是把数组先分解成一个一个有序的数字，然后两个两个合并，然后四个四个合并........

直到全部合并完。

 public static void deComposeNoRecursion(int[] arr){
        int gap=1;//一个一个合并开始，一个gap的区间相当于一个要合并的数组

        while(gap<arr.length) {//需要合并的数组，长度没有到达整个要排序数组的长度，就一直分解，合并
            for (int i = 0; i < arr.length; i = i + gap * 2) {//因为不再是递归，所以循环退出条件是数组的长度
                //把两个区间(i到i+gap和i+gap+1到i+gap+gap)合并完，再去到另一个区间合并，所以i=i+gap*2

                //定义： 两个要合并的数组，下标区间是[left,right]
                //我们只要不断地去分割区间（每次循环完，区间倍增），然后合并，即可实现排序
                int left = i;

                int right = left + gap * 2 - 1;//按照直觉好似是left+gap*2，但是实际上还要-1才行，因为left已经算是一个了
                int mid=(right+left)/2;//两个下标的中间值

                //注意按照for循环走，right和mid是有可能越界的，想要解决这个问题也很简单:
                if(mid>=arr.length)mid=arr.length-1;
                if(right>=arr.length)right=arr.length-1;//直接赋值最后一个元素即可，等一下也会自动合并这个数组

                mergeArr(arr,left,right,mid);//合并

            }
            gap*=2;//for循环结束，说明两个gap区间的数已经有序了，所以两个gap区间的数，可以看成一个区间了
        }

    }