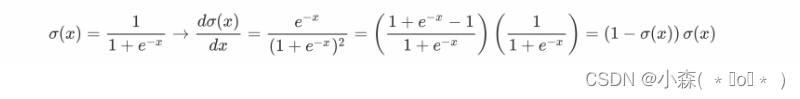【人工智能基础】逻辑回归实验分析

news2024/12/28 4:11:20

实验环境：anaconda、jutpyter Notebook

实验使用的库：numpy、matplotlib

一、逻辑回归

逻辑回归是一个常用于二分类的分类模型。本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

二、实验准备

引入库、预设值图像参数和随机种子
加载数据集：实验中使用到的是鸢尾花数据集

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
np.random.seed(42)

# 加载鸢尾花数据集
from sklearn import datasets
iris = datasets.load_iris()
# 查看数据集有哪些属性
print(list(iris.keys()))
print()
# 查看数据集的描述
print(iris.DESCR)

三、sigmoid函数

Logistic 分布是一种连续型的概率分布，其分布函数为

F(x) = P(X ≤ x) = 1 / (1 + e^(-(x-μ)/γ)

可以绘制除sigmoid函数的图像

# sigmoid函数
t = np.linspace(-10,10,100)
# σ(t) = 1 / (1 + e^(-t))
sig = 1 / (1 + np.exp(-t))
plt.figure(figsize=(9,3))
# 绘制参考线
plt.plot([-10,10],[0,0],"k-")
plt.plot([-10,10],[0.5,0.5],"k:")
plt.plot([-10,10],[1,1],"k:")
plt.plot([0,0],[-1.1,1.1],"k-")
# 绘制图像
plt.plot(t,sig,"b-",linewidth=2,label=r"$\sigma(t)=\frac{1}{1 + e^{-t}}$")
plt.xlabel("t")
plt.legend(loc="upper left", fontsize=20)
plt.axis([-10,10,-0.1,1.1])
plt.title("Figure 4-21. Logistic function")
plt.show()

sigmoid函数图像

四、单参数逻辑回归

提取参数x和标签y

# 截取数据第4列至最后一列的全部行数据
# 截取其中一个特征
x = iris['data'][:,3:]
# 设置类别为2(Virginica)的数据记为1，其他的两种记为0
y = (iris['target'] == 2).astype(np.int32)

训练模型

# 训练模型
from sklearn.linear_model import LogisticRegression
log_res = LogisticRegression()
log_res.fit(x,y)

使用模型进行预测

这里没有使用predcit函数来获取最终结果
而是使用predict_proba来获取数据在每个类下的概率，

# 创建测试数据，为1000*1的矩阵
x_test = np.linspace(0,3,1000).reshape(-1,1)
# 获取预测的概率值
y_proba = log_res.predict_proba(x_test)

单参数预测概率

矩阵一行的两个值分别代表0和1的概率，即Not Virginica和Virginica的概率

绘制预测曲线

plt.figure(figsize=(12,4))
plt.plot(x_test,y_proba[:,1],'g-',label='Virginica')
plt.plot(x_test,y_proba[:,0],'b--',label='Not Virginica')
# 找到分界线
decision_boundary = x_test[y_proba[:,1] >= 0.5][0][0]
plt.plot([decision_boundary,decision_boundary],[-1,2],'k:',linewidth=2)
# 绘制箭头
plt.arrow(decision_boundary, 0.08, -0.3, 0,head_width=0.05, head_length=0.1, fc='b',ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0,head_width=0.05, head_length=0.1, fc='g',ec='g')
plt.axis([0,3,-0.02,1.02])
plt.text(decision_boundary,0.15,'Decision Boundary',fontsize=16,ha='center')
plt.xlabel('Peta Width(cm)')
plt.ylabel('y_proba')
plt.legend(loc='center left')

单参数预测曲线

五、多参数逻辑回归

参数获取

# 截取两个维度的参数
x = iris['data'][:,(2,3)]
# 目标值
y = (iris['target'] == 2).astype(np.int32)

训练模型

# 训练逻辑回归模型
from sklearn.linear_model import LogisticRegression
log_res = LogisticRegression()
log_res.fit(x,y)

额外：如何构建一个点阵

我们选取了两个x参数和一个目标值y，即形成的结果需要有三个轴，对于x0，x1所在的平面上选取到一个点，可以找到与之对应的y值。所以为了绘制y轴上的图像（我们最终使用x0ox1平面上的等高线投影来代表y），我们需要找到众多的点(x0,x1)

可以使用如下的方式来获取这样的(x0,x1)点阵

x0,x1 = np.meshgrid(np.linspace(1,2,2).reshape(-1,1),
           np.linspace(10,12,3).reshape(-1,1))
# 构建列相同数据
print('x0',x0)
print()
# 构建行相同数据
print('x1',x1)
print()
# 拉长数据后拼接
print(np.c_[x0.ravel(),x1.ravel()])

我们可以发现meshgrid
返回的第一个值x0就是一个根据入参1得到的列相同矩阵，
返回的第二个值x1就是一个根据入参2得到的行相同矩阵
当我们使用ravel函数把矩阵拉长（平铺成一维数组），再拼接起来，就可以得到一个点阵

点阵构建演示

选取x0ox1面上的点以及对应的预测值

x0,x1 = np.meshgrid(np.linspace(2.9,7,500).reshape(-1,1),
           np.linspace(0.8,2.7,200).reshape(-1,1))
x_test = np.c_[x0.ravel(),x1.ravel()]

y_proba = log_res.predict_proba(x_test)

绘制概率等高线图

plt.figure(figsize=(10,4))
# Not Virginica的参数用蓝色方块表示
plt.plot(x[y==0,0],x[y==0,1],'bs')
# Virginica的参数用三角形表示
plt.plot(x[y==1,0],x[y==1,1],'g^')
# 绘制等高线，等高线表示概率
z = y_proba[:,1].reshape(x0.shape)
contour = plt.contour(x0,x1,z,cmap=plt.cm.brg)
plt.clabel(contour, inline=1)

plt.axis([2.9,7,0.8,2.7])
plt.text(3.5,1.5,'NOT Vir',fontsize=16, color='b')
plt.text(6.5,2.3,'Vir',fontsize=16, color='g')