Atcoder Beginner Contest351 A-E Solution题解

文章目录

[A - The bottom of the ninth](https://atcoder.jp/contests/abc351/tasks/abc351_a)
[B - Spot the Difference ](https://atcoder.jp/contests/abc351/tasks/abc351_b)
[D - Grid and Magnet](https://atcoder.jp/contests/abc351/tasks/abc351_d)
E

Note：省略模板代码，模版代码在末尾

A - The bottom of the ninth

题目：
给两个序列A和B，求B总和比A总和大时需要加上的最小值

思路：
答案=A总和-B总和+1

static void solve() throws IOException {
    int[] a = pIntArray(0);
    int[] b =pIntArray(0);
    int acnt = 0, bcnt = 0;
    for (int i = 0; i < a.length;  i++) {
        acnt += a[i];
    }
    for (int i = 0; i < b.length; i ++) {
        bcnt += b[i];
    }
    out.println(acnt - bcnt + 1);
}

B - Spot the Difference

题目：
给两个仅包含小写字母的NxN矩阵，找出唯一不同字母的下标对

思路：
模拟

static void solve() throws IOException {
    int n = pInt(in.readLine());
    String[] a = new String[n], b = new String[n];
    for (int i = 0; i < n; i++) {
        a[i] = in.readLine();
    }
    for (int i = 0; i < n; i++) {
        b[i] = in.readLine();
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (a[i].charAt(j) != b[i].charAt(j)) {
                out.println(i + 1 + " " + (j + 1) );
                return;
            }
        }
    }
}

C - Merge the balls

题目：
给一个空序列和N个球，第i个球的大小为 $2^{A_i}$ ；执行N次操作，在第i次操作时将第i个球加入到序列的最右边，然后重复以下步骤：当序列有两个及以上的球且最右边的两个球大小相同时，移去这两个球，并加入一个球，其大小为移除的球大小的总和，直到不能执行该步骤为止；

求执行完N次操作后序列还有多少个球

思路：
模拟

static void solve() throws IOException {
    int n = pInt(in.readLine());
    long[] balls = pLongArray(1);
    long[] t = new long[n + 1];
    int hh = 0;
    for (int i = 1; i <= n; i ++) {
        t[++ hh] = balls[i];
        while (hh > 1 && t[hh] == t[hh - 1]) {
            t[hh - 1] += 1;
            hh -= 1;
        }
    }
    out.println(hh);
}

D - Grid and Magnet

题目：
一个HxW的矩阵，某些格子里面会有磁铁，用 # 表示，其余格子为空，用. 表示；
如果在一个有磁铁的格子旁边，则无法继续移动；
问在这个矩阵里面的某个点出发能够移动的最大单元格数量；

思路：
实际上是求最大的连通块的格子数量，但连通块中边缘是一些磁铁，那么可以标记一下磁铁旁边的空单元格，当走到该种单元格时无法继续移动；
剩下的只需要用 BFS 来求连通块的大小即可；

static final int EMPTY = 0;
static final int MAGNET = 1;
static final int STICK = 2;
static final int[] d = new int[] {0, -1, 0, 1, 0};
static int bfs(int h, int w, int sx, int sy, int[][] vis) {
    Queue<int[]> q = new LinkedList<>();
    q.offer(new int[] {sx, sy});
    final int CURRENT_VISITED = 1010 * (sx + 1) + sy;
    vis[sx][sy] = CURRENT_VISITED;
    int ans = 0;
    while (!q.isEmpty()) {
        int[] u = q.poll();
        int x = u[0], y = u[1];
        ans ++;
        for (int i = 0; i < 4; i ++) {
            int dx = x + d[i], dy = y + d[i + 1];
            if (dx < 0 || dx >= h || dy < 0 || dy >= w || vis[dx][dy] == MAGNET || vis[dx][dy] == CURRENT_VISITED) continue;
            if (vis[dx][dy] == EMPTY) {
                q.offer(new int[] {dx, dy});
                vis[dx][dy] = CURRENT_VISITED;
            } else if (vis[dx][dy] != MAGNET && vis[dx][dy] != CURRENT_VISITED) {
                ans ++;
                vis[dx][dy] = CURRENT_VISITED;
            }
        }
    }
    return ans;
}
static void solve() throws IOException {
    String[] ins = pStringArray();
    int h = pInt(ins[0]), w = pInt(ins[1]);
    char[][] map = new char[h][w];
    int[][] vis = new int[h][w];
    for (int i = 0; i < h; i ++) {
        char[] t = in.readLine().toCharArray();
        System.arraycopy(t, 0, map[i], 0, w);
        for (int j = 0; j < w; j ++) {
            if (map[i][j] == '#') {
                vis[i][j] = MAGNET;
                for (int k = 0; k < 4; k++) {
                    int dx = i + d[k], dy = j + d[k + 1];
                    if (dx < 0 || dx >= h || dy < 0 || dy >= w) continue;
                    if (vis[dx][dy] == EMPTY) {
                        vis[dx][dy] = STICK;
                    }
                }
            }
        }
    }
    int ans = 1;
    for (int i =  0; i < h; i ++) {
        for (int j = 0; j < w; j ++) {
            if (vis[i][j] == EMPTY) {
                ans = Math.max(ans, bfs(h, w, i, j, vis));
            }
        }
    }
    out.println(ans);
}

E

题目：
在二维坐标平面上有 N 个点，兔子只能走对角线，计算AB两个点之间的距离 $dist(P_A, P_B)$ 为：兔子从A点开始走对角线，到达B点的最小次数；求 $\sum^{N-1}_{i=1}\sum^{N}_{j=i + 1} dist(P_i, P_j)$

思路：

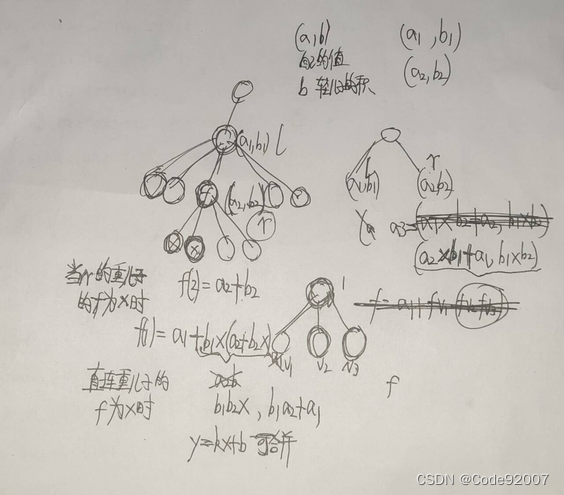
找规律，如下图，兔子从A点开始走，那么红色路线上的点都是可以到达的，注意到，可达点的坐标 $(x, y)$ 相加之后与起点A的坐标相加后模2同余，那么可以对此进行分类；

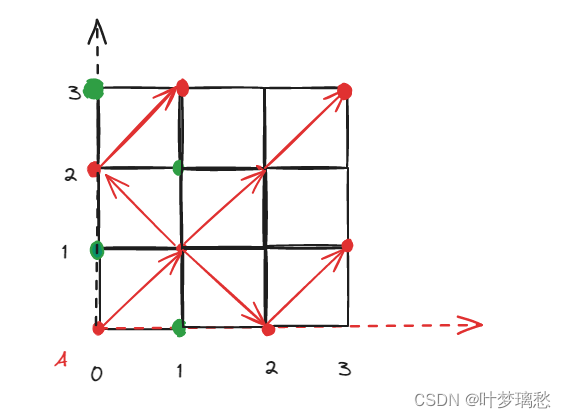
如何进行计算距离呢？
将二维坐标平面旋转45度(坐标可以变换为： $x^{'} = x + y, y^{'} = x - y$ )，兔子从走对角线就变成了上下左右走，两个点的距离就变成了水平方向和竖直方向上的距离了；

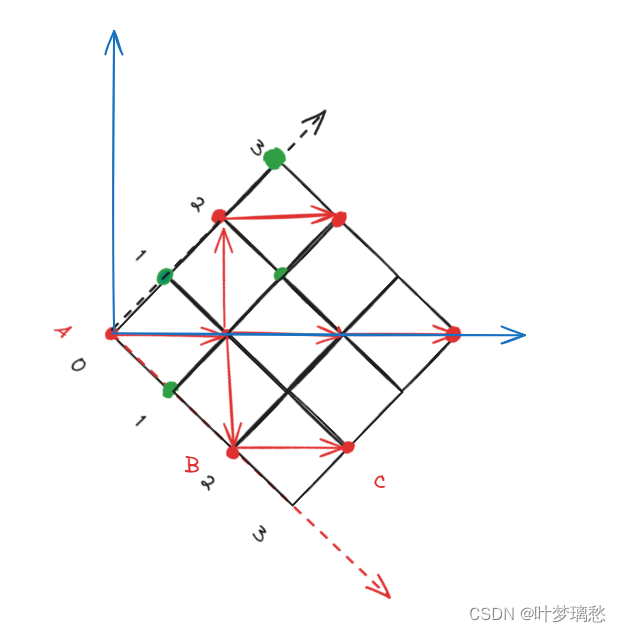
题目数据量是2e5，不可能两重循环来计算两个点的距离，这样会超时；
我们可以将x轴和y轴分开来计算：比如上面的A、B、C点

先计算x轴的，A到B的距离为1，B到C的距离为1，因为C点在A点的右边，那么A到C的距离为1+1=2
计算y轴的，A到B的距离为1

总的值就是3
需要注意的是，需要对转换后的x轴和y轴坐标排序，保证可以根据前面计算的距离来推出当前的距离（比如上面的A到C点）

static void solve() throws IOException {
    int n = pInt(in.readLine());
    List<Integer>[] px = new ArrayList[2];
    List<Integer>[] py = new ArrayList[2];
    for (int i = 0; i < 2; i ++) {
        px[i] = new ArrayList<>();
        py[i] = new ArrayList<>();
    }
    for (int i =0 ; i < n; i ++) {
        String[] ins = pStringArray();
        int x = pInt(ins[0]), y = pInt(ins[1]);
        int t = Math.abs(x + y) % 2;
        // 根据取模的结果分别拆分x轴和y轴
        px[t].add( x - y);
        py[t].add(x + y);
    }
    long ans = 0;
    for (int i = 0; i < 2; i ++) {
    	// 排序，保证坐标小的在前面
        px[i].sort(Comparator.comparingInt(a -> a));
        py[i].sort(Comparator.comparingInt(a -> a));
        int size = px[i].size();
        long sum1 = 0, sum2 = 0;
        for (int j = 0; j < size; j ++) {
        	// 当前点到前面其他点位置的距离
            ans += (long) j * (px[i].get(j) + py[i].get(j)) - sum1 - sum2;
            sum1 += px[i].get(j);
            sum2 += py[i].get(j);
        }
    }
    // 要求的值是 0->N-1, i+1->N-1 所以除以2
    out.println(ans / 2);
}

模版代码：

import java.io.*;
import java.nio.file.Files;
import java.nio.file.Paths;

public class Example {

    static void solve() throws IOException {

    }

    public static void main(String[] args) throws IOException {
        int t = 1;
//        t = Integer.parseInt(in.readLine());
        while (t -- > 0) {
            solve();
        }
        in.close();
        out.flush();
        out.close();
    }

    private static InputStream is = System.in;
    static {
        try {
            is = Files.newInputStream(Paths.get("F:\\Notes\\Algorithm\\Problems\\java\\java\\src\\main\\java\\input.txt"));
        } catch (Exception e) {
            is = System.in;
        }
    }
    private static final BufferedReader in = new BufferedReader(new InputStreamReader(is));
    private static final PrintWriter out = new PrintWriter(System.out);
    private static int pInt(String s) {
        return Integer.parseInt(s);
    }
    private static long pLong(String s) {
        return Long.parseLong(s);
    }
    private static String[] pStringArray() throws IOException {
        return in.readLine().split(" ");
    }
    private static int[] pIntArray(int start) throws IOException {
        String[] s = pStringArray();
        int[] arr = new int[start + s.length];
        for (int i = start, j = 0; i < arr.length; i++, j ++) {
            arr[i] = Integer.parseInt(s[j]);
        }
        return arr;
    }

    private static long[] pLongArray(int start) throws IOException {
        String[] s = pStringArray();
        long[] arr = new long[start + s.length];
        for (int i = start, j = 0; i < arr.length; i++, j ++) {
            arr[i] = Long.parseLong(s[j]);
        }
        return arr;
    }
}