题目

n(n<=2e5)个点,给定一个长为a的初始权值数组,
以1为根有根树,
树哈希值f计算如下:
(1)如果一个点u是叶子节点,则f[u]=a[u]
(2)否则,
q(q<=2e5)次点权修改,每次问修改之后根节点(点1)的树哈希值f
思路来源
qiuzx_代码
题解
新开一个口胡题解专栏,记录当前题目水平不在我能力范围之内
但是看别人的代码能看懂,自己写可能要调一万年的这种题,描述一下他是怎么写的
心得
动态 DP - OI Wiki
动态dp可以参考这篇,
基本是对于有根树树形dp,想动态获取根节点的dp值,dp值和树上点权相关,点权带修,
序列的动态dp,一般是线段树维护矩阵乘法(可广义换成其他运算)或线段树节点合并
树上版本,是树剖维护矩阵转移或者线段树节点
本题中,先树链剖分,求出重儿子,重链维护线段树
线段树上每个节点维护一个y=bx+a的点对(a,b),
其中,b是f值非零的轻儿子的f积,x是重儿子的f值(未知,待代入)
a是当前节点u的a[u]值 ,然后就能b1*(b2x+a2)+a1这么线段树往上合并了
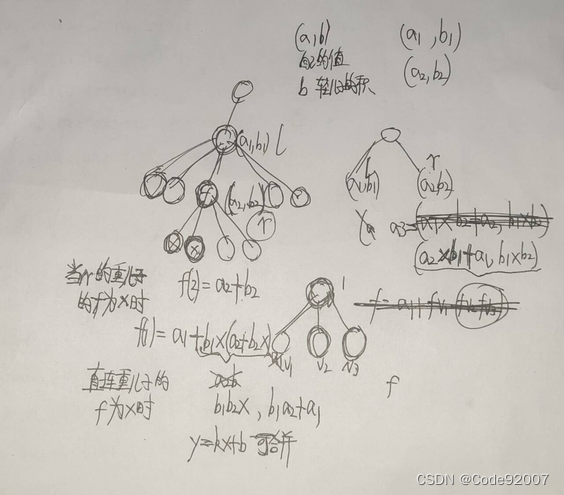
递归到叶子的时候,由于叶子不存在重儿子,x值为0,
所以链头的f值,就是当线段树区间[l,r],
l为重链头的dfs序,r为叶子重链尾的dfs序时,这个区间节点对应的(a,b)中a的值
由于为0的值会对运算值有影响,并且儿子f值从一个0变成没有0的时候难以恢复之前的乘积,
所以单独记录0的个数,所以变更的时候,动态记录链头点的f值为0的儿子的数量
代码
qiuzx_代码
//ANMHLIJKTJIY!
#pragma GCC optimize(2)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline","fast-math","unroll-loops","no-stack-protector")
#pragma GCC diagnostic error "-fwhole-program"
#pragma GCC diagnostic error "-fcse-skip-blocks"
#pragma GCC diagnostic error "-funsafe-loop-optimizations"
#include <bits/stdc++.h>
#define INF 1000000000
#define LINF 1000000000000000000
#define MOD 1000000007
#define mod 998244353
#define F first
#define S second
#define ll long long
#define N 200010
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
using namespace std;
char buf[1<<23],*p1=buf,*p2=buf;
ll rint(){
ll ret=0;
char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) ret=ret*10+(c-'0'),c=getchar();
return ret;
}
ll ksm(ll x,ll y)
{
ll ret=1;
while(y>0)
{
if(y&1)
{
ret=(ret*x)%mod;
}
x=(x*x)%mod;
y>>=1;
}
return ret;
}
struct Node{
ll a,b;
Node(){a=b=0;}
Node(ll _a,ll _b){a=_a,b=_b;}
Node operator + (const Node &x)const{
return Node((a*x.b+x.a)%mod,(b*x.b)%mod);
}
};
struct SegT{
ll lo[N<<2],hi[N<<2],pa[N],pb[N];
Node val[N<<2];
void build(ll x,ll l,ll r)
{
lo[x]=l,hi[x]=r;
if(l==r)
{
val[x]=Node(pa[l],pb[l]);
return;
}
ll mid=(l+r)>>1,a=x<<1;
build(a,l,mid);
build(a|1,mid+1,r);
val[x]=val[a|1]+val[a];
return;
}
void update(ll x,ll l,Node v)
{
ll tl=lo[x],tr=hi[x];
if(tl==tr)
{
val[x]=v;
return;
}
ll mid=(tl+tr)>>1,a=x<<1;
if(mid>=l)
{
update(a,l,v);
}
else
{
update(a|1,l,v);
}
val[x]=val[a|1]+val[a];
return;
}
Node query(ll x,ll l,ll r)
{
ll tl=lo[x],tr=hi[x];
if(l<=tl&&tr<=r)
{
return val[x];
}
ll mid=(tl+tr)>>1,a=x<<1;
if(mid>=r)
{
return query(a,l,r);
}
if(mid<l)
{
return query(a|1,l,r);
}
return query(a|1,l,r)+query(a,l,r);
}
}segt;
ll n,q,fa[N],a[N],b[N],f[N],num0[N],dfn[N],dcnt=0,tp[N],lw[N],sz[N],hson[N];
vector<ll> vt[N];
void predfs(ll x)
{
ll i;
sz[x]=1,hson[x]=-1;
for(i=0;i<vt[x].size();i++)
{
predfs(vt[x][i]);
sz[x]+=sz[vt[x][i]];
if(hson[x]==-1||sz[hson[x]]<sz[vt[x][i]])
{
hson[x]=vt[x][i];
}
}
return;
}
void dfs(ll x,bool ist=true)
{
tp[x]=ist?x:tp[fa[x]];
dfn[x]=++dcnt;
b[x]=1;
if(hson[x]!=-1)
{
dfs(hson[x],false);
lw[x]=lw[hson[x]];
f[x]=f[hson[x]];
}
else
{
lw[x]=x;
f[x]=a[x];
return;
}
ll i;
for(i=0;i<vt[x].size();i++)
{
if(vt[x][i]!=hson[x])
{
dfs(vt[x][i]);
f[x]=(f[x]*f[vt[x][i]])%mod;
if(f[vt[x][i]])
{
b[x]=(b[x]*f[vt[x][i]])%mod;
}
else
{
num0[x]++;
}
}
}
f[x]=(f[x]+a[x])%mod;
return;
}
ll calc(ll x)
{
Node cur=segt.query(1,dfn[x],dfn[lw[x]]);
return cur.a;
}
int main(){
ll i,x,y;
n=rint(),q=rint();
for(i=1;i<n;i++)
{
fa[i]=rint()-1;
vt[fa[i]].push_back(i);
}
fa[0]=-1;
for(i=0;i<n;i++)
{
a[i]=rint();
}
predfs(0);
dfs(0);
for(i=0;i<n;i++)
{
segt.pa[dfn[i]]=a[i];
segt.pb[dfn[i]]=num0[i]?0:b[i];
}
segt.build(1,1,n);
while(q--)
{
x=rint()-1,y=rint();
a[x]=y;
segt.update(1,dfn[x],Node(a[x],num0[x]?0:b[x]));
while(true)
{
ll pre=f[tp[x]];
f[tp[x]]=calc(tp[x]);
x=tp[x];
if(fa[x]<0)
{
break;
}
if(pre)
{
b[fa[x]]=(b[fa[x]]*ksm(pre,mod-2))%mod;
}
else
{
num0[fa[x]]--;
}
if(f[x])
{
b[fa[x]]=(b[fa[x]]*f[x])%mod;
}
else
{
num0[fa[x]]++;
}
x=fa[x];
segt.update(1,dfn[x],Node(a[x],num0[x]?0:b[x]));
}
printf("%lld\n",f[0]);
}
return 0;
}