神经网络的优化器是用于训练神经网络的一类算法,它们的核心目的是通过改变神经网络的权值参数来最小化或最大化一个损失函数。优化器对损失函数的搜索过程对于神经网络性能至关重要。
作用:
-
参数更新:优化器通过计算损失函数相对于权重参数的梯度来确定更新参数的方向和步长。
-
收敛加速:高效的优化算法可以加快训练过程中损失函数的收敛速度。
-
避免陷入局部最优:一些优化器特别设计了策略(如动量),以帮助模型跳出局部最小值,寻找到更全局的最优解。
-
适应性调整:许多优化器可以自适应地调整学习率,使得训练过程中对不同的数据或参数具有不同的调整策略。
常用优化器有以下几种:
-
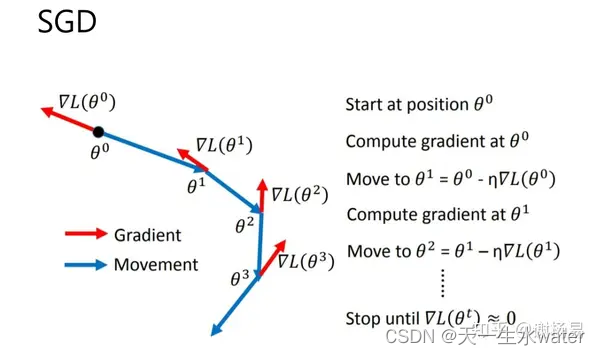
梯度下降(SGD):最基本的优化策略,它使用固定的学习率更新所有的权重。存在批量梯度下降(使用整个数据集计算梯度)、随机梯度下降(每个样本更新一次权重)和小批量梯度下降(mini-batch,每个小批量数据更新一次权重)。
import torch import torch.nn as nn import torch.optim as optim # 假设我们有一个简单的模型 model = nn.Sequential( nn.Linear(10, 5), nn.ReLU(), nn.Linear(5, 1) ) # 定义损失函数,这里使用均方误差 loss_fn = nn.MSELoss() # 定义优化器,使用 SGD 并设置学习率 optimizer = optim.SGD(model.parameters(), lr=0.01) # 假定一个输入和目标输出 input = torch.randn(64, 10) target = torch.randn(64, 1) # 运行模型训练流程 for epoch in range(100): # 假设总共训练 100 轮 # 正向传播,计算预测值 output = model(input) # 计算损失 loss = loss_fn(output, target) # 梯度清零,这一步很重要,否则梯度会累加 optimizer.zero_grad() # 反向传播,计算梯度 loss.backward() # 根据梯度更新模型参数 optimizer.step() # 记录、打印损失或者使用损失进行其他操作 -
带动量的SGD(Momentum):在传统的梯度下降算法基础上,SGD Momentum考虑了梯度的历史信息,帮助优化器在正确的方向上加速,并且抑制震荡。
-
Adagrad:自适应地为每个参数分配不同的学习率,从而提高了在稀疏数据上的性能。对于出现次数少的特征,会给予更大的学习率。
-
RMSprop:对Adagrad进行改进,通过使用滑动平均的方式来更新学习率,解决了其学习率不断减小可能会提前停止学习的问题。
-
Adam(Adaptive Moment Estimation):结合Momentum和RMSprop的概念,在Momentum的基础上计算梯度的一阶矩估计和二阶矩估计,进而进行参数更新。
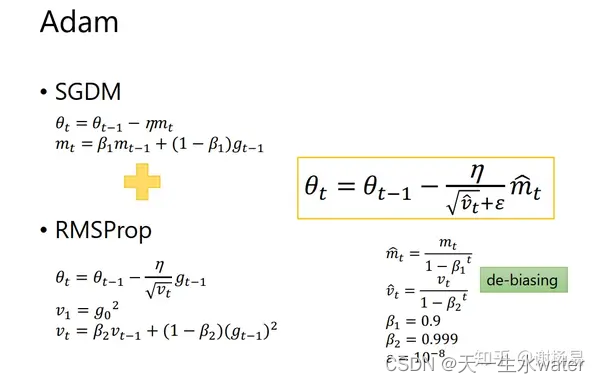
作用: 自适应学习率调整:Adam算法通过自适应地调整每个参数的学习率,使得对于不同的参数,学习率能够根据其梯度的大小进行动态调整。这样能够更快地收敛到最优解,同时减少了手动调整学习率的需求。 动量优化:Adam算法利用动量的概念来加速优化过程。动量能够帮助算法在参数空间中跨越局部极小值,从而加速收敛过程,并且可以在参数更新时减少梯度方向上的震荡。 参数更新:Adam算法使用指数加权移动平均来估计每个参数的一阶矩(梯度的均值)和二阶矩(梯度的方差),然后根据这些估计值来更新参数。 import torch import torch.nn as nn import torch.optim as optim # 定义一个简单的神经网络 class Net(nn.Module): def __init__(self): super(Net, self).__init__() self.fc1 = nn.Linear(784, 256) self.fc2 = nn.Linear(256, 128) self.fc3 = nn.Linear(128, 10) def forward(self, x): x = torch.flatten(x, 1) x = torch.relu(self.fc1(x)) x = torch.relu(self.fc2(x)) x = self.fc3(x) return x # 初始化模型和Adam优化器 model = Net() optimizer = optim.Adam(model.parameters(), lr=0.001) # 定义损失函数 criterion = nn.CrossEntropyLoss() # 训练过程示例 for epoch in range(num_epochs): for inputs, targets in train_loader: optimizer.zero_grad() outputs = model(inputs) loss = criterion(outputs, targets) loss.backward() optimizer.step() 在这个示例中,我们首先定义了一个简单的神经网络模型(包含三个全连接层),然后初始化了Adam优化器,将模型的参数传递给优化器。在训练过程中,我们在每个迭代周期中执行了模型的前向传播、损失计算、反向传播以及参数更新的操作。通过调用optimizer.step()来实现参数更新,Adam优化器会根据当前梯度自适应地调整学习率,并更新模型参数。 -
Nadam:结合了Adam和Nesterov动量的优化器,它在计算当前梯度前先往前走一小步,用来修正未来的梯度方向。
-
AdaDelta:是对Adagrad的扩展,减少了学习率递减的激进程度。
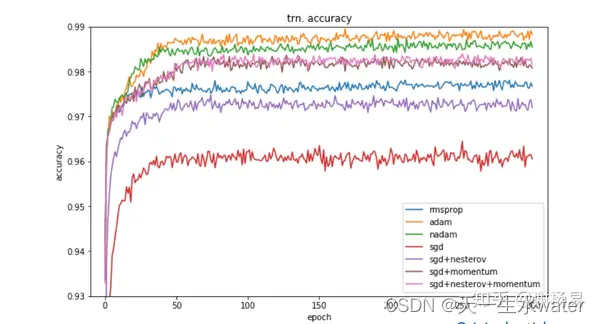
不同的优化器可能会对神经网络的训练效果产生较大影响,因此在实际应用中,我们通常会根据具体问题来选择最合适的优化器。实际选择时,往往需要进行试验,并通过验证集的性能来调整选择。

有人研究过几大优化器在一些经典任务上的表现。如下是在图像分类任务上,不同优化器的迭代次数和ACC间关系。