数学视角下的编程艺术：深入线性代数学习与应用

作者介绍：10年大厂数据\经营分析经验，现任大厂数据部门负责人。
会一些的技术：数据分析、算法、SQL、大数据相关、python
欢迎加入社区：码上找工作
作者专栏每日更新：
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化：企业实战案例
python源码解读
备注说明：方便大家阅读，统一使用python，带必要注释，公众号数据分析螺丝钉一起打怪升级

思路良久准备一篇详细的关于线性代数及其在编程中应用的文章。数学基础是技术同学的前进的基石，我们将从线性代数的基本概念开始，然后逐渐深入到具体的应用案例和代码实现。

第一部分：线性代数基础

1. 向量和向量空间

定义：

向量：向量是线性代数中的基本元素，可以视为空间中的一个点或箭头，具有大小和方向。在数学和编程中，向量通常表示为一组数字，这组数字定义了向量在多维空间中的方向和长度。
向量空间：一个向量空间是一组向量的集合，这些向量可以进行加法和标量乘法运算，并且运算结果仍然在这个集合中。

基本操作：
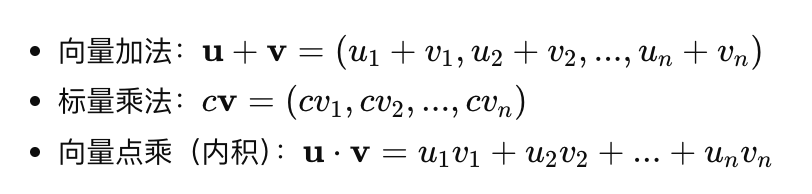
在这里插入图片描述

Python代码示例：向量加法和点乘

import numpy as np

# 向量定义
u = np.array([2, 3])
v = np.array([5, 1])

# 向量加法
vector_addition = u + v

# 点乘
dot_product = np.dot(u, v)

print("向量加法结果:", vector_addition)
print("点乘结果:", dot_product)

2. 矩阵及其运算

定义：

矩阵：矩阵是一个由行和列组成的矩形数组，矩阵中的每个元素可以是数字或算术表达式。

基本操作：

矩阵加法：两个矩阵的对应元素相加。
矩阵乘法：矩阵的乘法不是元素对应相乘，而是第一个矩阵的行与第二个矩阵的列的点乘。
矩阵转置：将矩阵的行转换成列。

Python代码示例：矩阵乘法和转置

import numpy as np

# 矩阵定义
A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 0], [1, 3]])

# 矩阵乘法
matrix_multiplication = np.dot(A, B)

# 矩阵转置
transpose = np.transpose(A)

print("矩阵乘法结果:\n", matrix_multiplication)
print("矩阵转置:\n", transpose)

为了全面深入地探讨线性代数在编程中的应用，以下是接下来文章的详细目录：

第二部分：线性变换和矩阵应用

在这一部分，我们将深入探讨线性变换的概念以及矩阵如何在图像处理等应用中实现这些变换。线性变换是线性代数中的一个核心主题，它提供了一种强大的方法来描述和实现变换，包括旋转、缩放和映射等。

3. 线性变换

定义和重要性

线性变换是从一个向量空间到另一个向量空间的函数，满足两个性质：加法性和齐次性。简单地说，线性变换可以将一组坐标点通过特定的数学规则转换到新的位置，这对于图形编程、物理模拟等领域至关重要。

线性变换的基本性质

加法性：( T(u + v) = T(u) + T(v) ) 对所有 ( u, v ) 成立。
齐次性：( T(au) = aT(u) ) 对所有标量 ( a ) 和向量 ( u ) 成立。

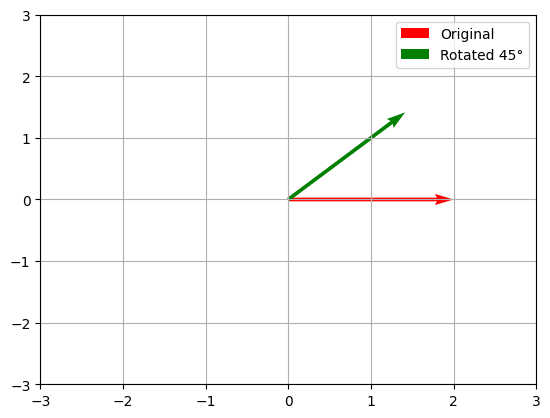
实现线性变换的代码示例

在Python中使用NumPy库，可以方便地演示线性变换：

import numpy as np
import matplotlib.pyplot as plt

# 定义一个线性变换：旋转变换
def rotate(theta):
    theta = np.radians(theta)
    c, s = np.cos(theta), np.sin(theta)
    return np.array([[c, -s], [s, c]])

# 创建一个向量
v = np.array([2, 0])

# 应用一个45度旋转
rotation_matrix = rotate(45)
v_rotated = np.dot(rotation_matrix, v)

# 可视化结果
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='r', label='Original')
plt.quiver(0, 0, v_rotated[0], v_rotated[1], angles='xy', scale_units='xy', scale=1, color='g', label='Rotated 45°')
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.grid()
plt.legend()
plt.show()

在这里插入图片描述

4. 矩阵在图像处理中的应用

矩阵在图像处理中的应用非常广泛，特别是在图像变换方面，如缩放、旋转和反射等。

图像的表示为矩阵

在计算机图像处理中，图像通常表示为像素矩阵。每个元素代表一个像素点的颜色值。

图像缩放、旋转和反射的矩阵运算

缩放：通过乘以一个缩放矩阵来实现。
旋转：通过乘以一个旋转矩阵来实现，如上面的示例。
反射：通过乘以特定的反射矩阵来实现，通常是沿x轴或y轴。

Python中实现图像变换的示例

这里使用Python的PIL库来演示图像的基本变换：

from PIL import Image, ImageOps

# 打开一个图像文件
img = Image.open('path_to_image.jpg')

# 缩放图像
img_resized = img.resize((50, 50))

# 旋转图像
img_rotated = img.rotate(45)

# 显示图像
img.show()
img_resized.show()
img_rotated.show()

缩放图像
在这里插入图片描述
旋转图像

这部分内容提供了线性变换和矩阵在实际应用中的基础知识和示例，帮助理解其在科学计算和图像处理中的重要性。在接下来的部分，我们将探讨更多高级主题，包括特

征值和特征向量，以及这些概念如何应用于数据分析和机器学习中。

第三部分：特征值和特征向量

特征值和特征向量是线性代数中的重要概念，广泛应用于各种科学和工程领域，包括稳定性分析、振动分析、主成分分析（PCA）等。它们为理解和处理矩阵提供了强大的工具。

5. 特征值和特征向量

定义和直观理解

在这里插入图片描述

计算矩阵的特征值和特征向量

在这里插入图片描述

Python代码示例

使用NumPy库来计算矩阵的特征值和特征向量：

import numpy as np

# 定义一个矩阵
A = np.array([[4, 2], [1, 3]])

# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)

print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)

6. 主成分分析（PCA）

PCA的数学原理

主成分分析（PCA） 是一种统计方法，它使用正交变换来将一组可能相关的变量转换成一组线性不相关的变量，这组变量称为主成分。
PCA的核心是找到数据最大方差的方向，并将原数据投影到这些方向上。

如何使用PCA进行数据降维

计算数据的协方差矩阵。
计算协方差矩阵的特征值和特征向量。
将特征值按降序排列，选择最大的几个特征值及其对应的特征向量。
使用这些特征向量将原数据转换到新的子空间，这便完成了数据降维。

使用Python实现PCA

from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# 加载数据集
data = load_iris()
X = data.data

# 创建PCA实例
pca = PCA(n_components=2)  # 降至2维
X_pca = pca.fit_transform(X)

# 可视化
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=data.target)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA of IRIS Dataset')
plt.show()

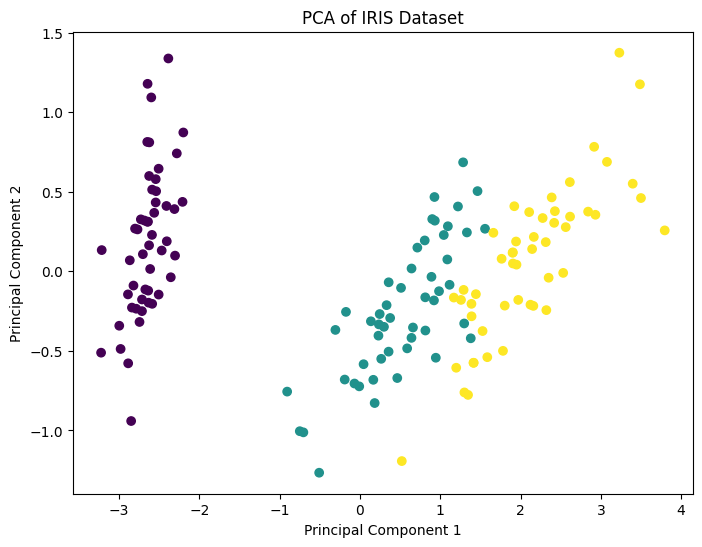
在这里插入图片描述
这张图代表了主成分分析（PCA）应用在IRIS数据集上的结果。在这个散点图中，每个点代表数据集中的一个样本，颜色可能代表样本的不同类别。

横轴（Principal Component 1）：表示数据在第一主成分方向上的投影值，这个方向捕获了数据最大的方差。
纵轴（Principal Component 2）：表示数据在第二主成分方向上的投影值，这个方向捕获了数据次大的方差，并且与第一主成分正交。
PCA通过这些主成分降低了数据的维度，同时尽可能保留了最多的信息。在此图中，可以看出，使用前两个主成分已经能够相对清晰地区分出不同的数据群。这在无监督学习、特征提取和数据可视化等方面是非常有用的。通过这种方式，我们可以更容易地识别出数据中的模式和结构。

在这一部分中，我们详细探讨了特征值和特征向量的概念，并通过PCA的实例展示了它们在数据分析中的应用。这些工具不仅能帮助我们更好地理解数据的内在结构，还能在减少数据复杂性方面发挥重要作用。接下来，我们将继续探讨

第四部分：线性代数在机器学习中的应用

线性代数是机器学习和数据科学的基础。从线性回归到深度学习，大多数机器学习算法都依赖于线性代数的概念。本部分将探讨线性代数在几个关键的机器学习应用中的作用。

7. 线性回归模型

线性回归的矩阵表示

线性回归是一种预测数值型数据的方法，其模型可以用矩阵和向量的形式表示。给定一个数据集，其中包含多个观测点，模型尝试找到最佳的线性关系来预测目标变量。

在这里插入图片描述

使用线性代数求解线性回归

线性回归的参数 ( \beta ) 可以通过最小化误差平方和来求解，通常使用矩阵的形式来进行：

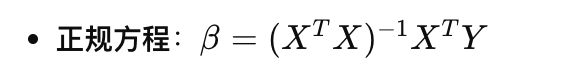
在这里插入图片描述

这一方法直接利用矩阵运算来找到使成本函数最小化的系数。

Python代码实现

import numpy as np

# 模拟数据
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
Y = np.dot(X, np.array([1, 2])) + 3

# 增加截距项
X_b = np.c_[np.ones((4, 1)), X]  # add x0 = 1 to each instance

# 计算最佳参数
beta_hat = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(Y)

print("计算得到的参数β:", beta_hat)

8. 神经网络的矩阵运算

神经网络中的权重和激活函数

神经网络由层组成，每层包含多个神经元。每个神经元的输出是其输入的加权和，通过一个非线性的激活函数进行转换。

权重矩阵：每一层的权重可以表示为一个矩阵，其中的元素表示前一层的神经元与当前层神经元之间的连接强度。

矩阵运算在前向传播中的作用

在神经网络中，前向传播的过程可以使用矩阵乘法来表示，这使得计算效率非常高。

在这里插入图片描述

用Python构建简单的神经网络

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 输入数据
X = np.array([0.5, -1.2])

# 权重和偏置
W1 = np.array([[0.1, 0.8], [0.4, -0.5]])
b1 = np.array([0.3, 0.9])

# 计算第一层输出
z1 = np.dot(W

1, X) + b1
a1 = sigmoid(z1)

print("激活值:", a1)