---

1.背景

2018年，D Binu等人受到骑手群体竞赛赢得比赛行为启发，提出了骑手优化算法（Rider Optimization Algorithm, ROA）。

2.算法原理

2.1算法思想

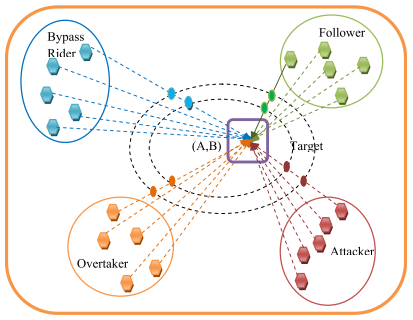
ROA基于骑手群体竞赛协同合作启发，探究如何赢得比赛，ROA主要分为四类：

• 绕行骑手（Bypass rider）：绕过主要路线到达目标，这意味着绕行骑手不跟随领头骑手（适应度最好） 避免陷入局部解
• 跟随骑手（Follower）：跟随骑手是指大部分依赖或跟随领头骑手
• 超车骑手（Overtaker）：按照领头骑手和自己位置前进
• 冲刺骑手（Attacker）：根据其他骑手的位置以最大速度到达目标

2.2算法过程

群体G分为绕行骑手B，跟随骑手F，超车骑手O，冲刺骑手A：
$$\begin{gathered} R=B+F+O+A \\ B=F=O=A=R/4\text{\hspace{1em}(1)} \end{gathered}$$
骑手参数初始化，辆在时刻T的转向角T为：
T t = { T i , j t } ; 1 ≤ i ≤ R ; 1 ≤ j ≤ Q (2) T_t=\{T_{i,j}^t\};\quad1\leq i\leq R; 1\leq j\leq Q\tag{2} Tt​={Ti,jt​};1≤i≤R;1≤j≤Q(2)
表达式为：
$$T_{i,j}=\{\begin{array}{ll}{\theta }_i;& \text{if}j=1\\ T_{i,j-1}+\phi ;& \text{if}j\ne 1\&T_{i,j-1}+\phi \le 360\\ T_{i,j-1}+\phi -360;& \text{otherwise}\end{array}\text{\hspace{1em}(3)}$$
其中θi是骑手车辆的位置角，φ是坐标角。骑手车辆的位置角度取决于骑手人数和360°的最大角度:
$${\theta }_i=i\ast \frac{360^{\circ }}{R}\text{\hspace{1em}(4)}$$
其中R是乘客的数量。坐标角有助于确定给定的转向角:
$$\phi =\frac{360}{Q}\text{\hspace{1em}(5)}$$
然后初始化与车辆相关的齿轮、油门、刹车等三个参数。在一个特定的组中，骑手的车辆的齿轮表示为:
E = { E i } ; 1 ≤ i ≤ R (6) E=\{E_i\};\quad1\leq i\leq R\tag{6} E={Ei​};1≤i≤R(6)
其中Ei是第i个骑手的车辆的齿轮。在时间t, Et i从集合{0,1,2,3,4}中取一个值。Ei的初始值设为零。同样，第二个参数，即车辆的油门初始化为：
e = { e i } ; 1 ≤ i ≤ R (7) e=\{e_i\};\quad1\leq i\leq R\tag{7} e={ei​};1≤i≤R(7)
其中ei表示车手车辆的油门，其取值范围为0到1。在时刻t, ei的初始值被设为零。以同样的方式，车辆中的制动器表示为：
K = { K i } ; 1 ≤ i ≤ R (8) K=\{K_i\};\quad1\leq i\leq R\tag{8} K={Ki​};1≤i≤R(8)
其中Ki为第i位骑行者车辆的制动，取值范围为[0,1]。Ki的初始值设置为1。在到达目标的路上，骑手根据空间中的两个边界值调整车辆(汽车/汽车)的速度。因此，骑手可以驾驶的最大速度为：
$$V_{\max }^i=\frac{X_U^i-X_L^i}{T_{\mathrm{OFF}}}\text{\hspace{1em}(9)}$$
车手的齿轮速度限制计算为:
$$V_i^E=\frac{V_{\max }^i}{|E|}\text{\hspace{1em}(10)}$$
初始化骑手组和参数后，计算每个骑手的成功率。成功率根据骑手位置与目标位置之间的距离来表示：
$$r_i=\frac{1}{\Vert X_i-L_T\Vert }\text{\hspace{1em}(11)}$$
由于绕行骑手绕过公共路径，不跟随领头骑手，因此该集合的位置更新是随机的，表示为:
$$X_{t+1}^B(i,j)=\delta [X_t(\eta ,j)\ast \beta (j)+X_t(\xi ,j)\ast [1-\beta (j)]]\text{\hspace{1em}(12)}$$
跟随骑手跟随领头骑手的位置更新自己的位置，使骑手能够快速有效地到达目标:
$$X_{t+1}^F(i,k)=X^L(L,k)+\left[\cos \left(T_{i,k}^t\right)\ast X^L(L,k)\ast d_i^t\right]\text{\hspace{1em}(13)}$$
k为坐标选择器，XL为领跑骑手的位置，L为领跑骑手的指数，Tt i,k为第i位骑手在第k个坐标上的转向角度，dt i为第i位骑手要行驶的距离。这个距离是用骑手的速度乘以离开时间的比率来测量:
$$d_i^t=v_i^t\ast (1/T_{\mathrm{OFF}})\text{\hspace{1em}(14)}$$
其中vt i是骑手i的速度，TOFF是脱离时间。骑手的速度与车辆的速度和骑手参数有关:
$$v_i^t=\frac{1}{3}[E_i^t\ast V_i^E+V_{\max }^i\ast e_i^t+(1-K_i^t)\ast V_{\max }^i]\text{\hspace{1em}(15)}$$
坐标选择器是根据准时概率选择：
$$P_{\mathrm{ON}}^t=\left(\frac{t}{T_{\mathrm{OFF}}}\right)\ast Q\text{\hspace{1em}(16)}$$
超车骑手位置更新:
$$X_{t+1}^O(i,k)=X_t(i,k)+\left[D_t^I(i)\ast X^L(L,k)\right]\text{\hspace{1em}(17)}$$
D为当前个体的方向指示器:
$$D_t^I(i)=\left[\frac{2}{1-\log \left(S_t^R(i)\right)}\right]-1\text{\hspace{1em}(18)}$$
其中SRt (i)为相对成功率，超车手的相对成功率由其适应度值与种群内最差个体的适应度值之比确定：
$$S_t^R(i)=\frac{r_t(i)}{{\max }_{i=1}^R{r}_t(i)}\text{\hspace{1em}(19)}$$
冲刺骑手位置更新:
$$X_{t+1}^A(i,j)=X^L(L,j)+\left[\cos \left(T_{i,j}^t\right)\ast X^L(L,j)\right]+d_i^t\text{\hspace{1em}(20)}$$

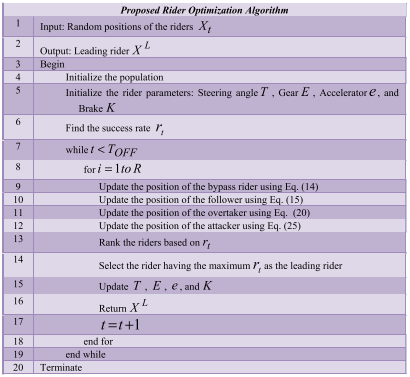
伪代码

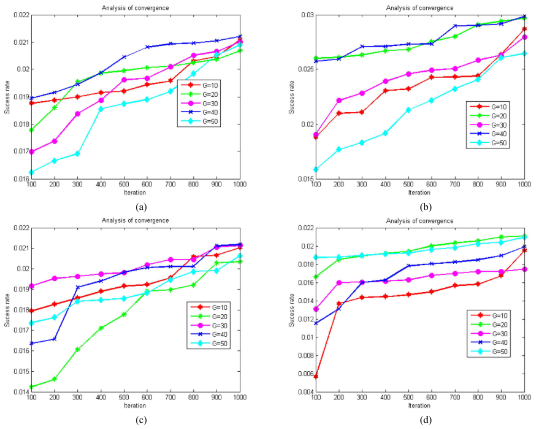
3.结果展示

4.参考文献

[1] Binu D, Kariyappa B S. RideNN: A new rider optimization algorithm-based neural network for fault diagnosis in analog circuits[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 68(1): 2-26.