目录
acwing-898数字三角形(模板题)
思路
注意点
代码
视频讲解推荐
2020蓝桥杯省赛-数字三角形
错误思路 (可不看)
思路
代码
注意点
续上之前的啦。
【第二十五课】动态规划:01背包问题(acwing-2 / 思路 / 含一维数组优化 / c++代码)
适合在学习过背包问题的基础上看这篇。
这里我们介绍线性dp:
线性动态规划通常用于解决具有线性结构的问题,例如序列或数组。这类问题的一个典型特点是,问题的解决方案可以通过其子问题的解决方案来构建。例如,如果我们要找到一个序列的最长递增子序列,我们可以通过查找每个子序列的最长递增子序列来找到整个序列的最长递增子序列。
acwing-898数字三角形(模板题)

思路
这道题题意不难理解,目的是 找到从第一行走到最后一行得到的和最大的这个最大值。要求是每一步都只能走距离该数最近的左下角和右下角的两个位置。
感觉在之前背包问题的基础上,这道题的思路还是很好理解的。就不多说了。
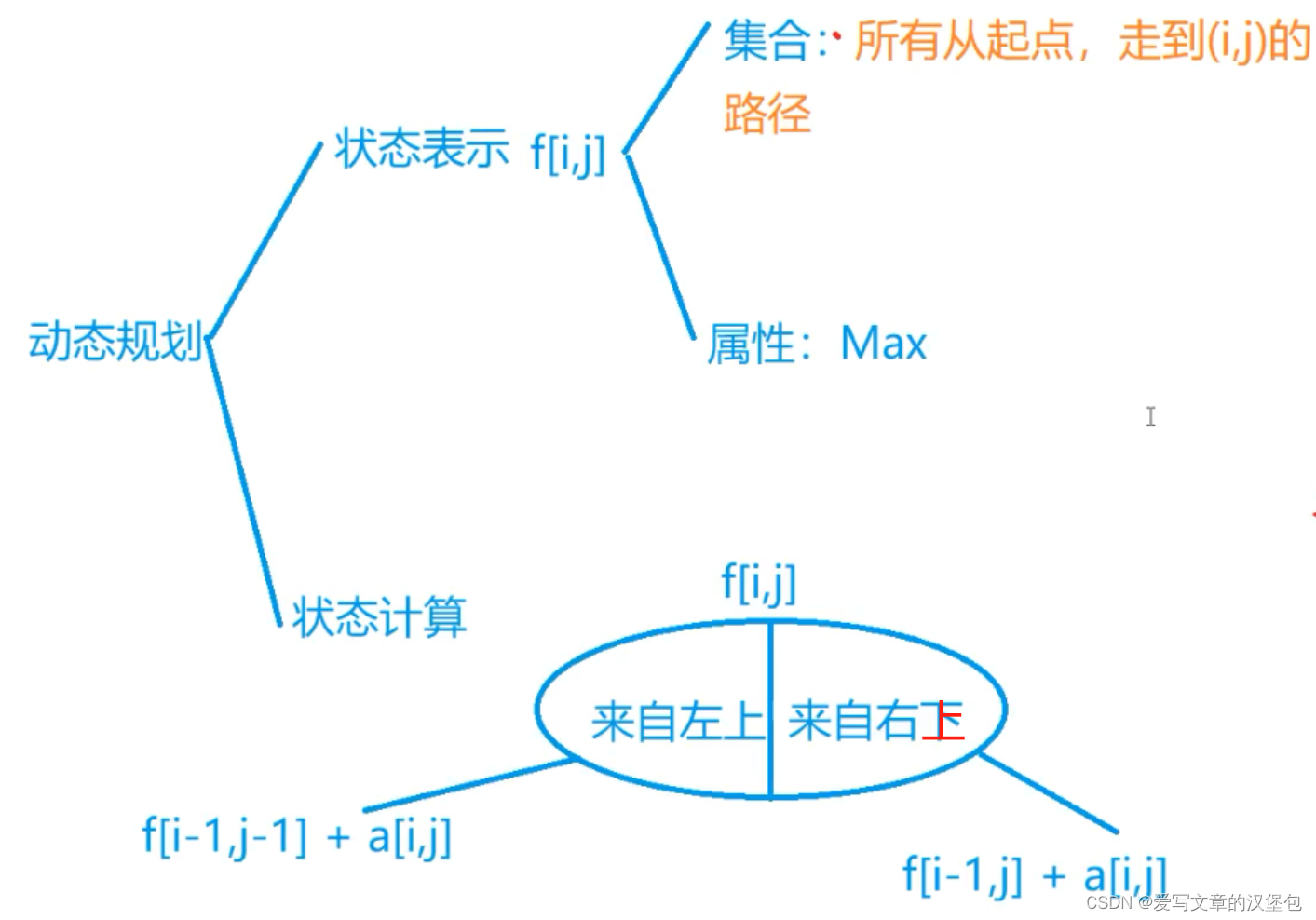
我们是要用二维数组来存储这个数字三角形的,为了方便表示,我们这样理解这个二维数组的行列:

斜着表示每一列。
这样的话对于题目要求的这个数只能从其最近的左上角和右上角到达,表示出这两个位置的值就可以实现我们的思路。所以我们这样定义行列可以方便我们表示这一步。
回顾一下之前的背包问题的分析图:
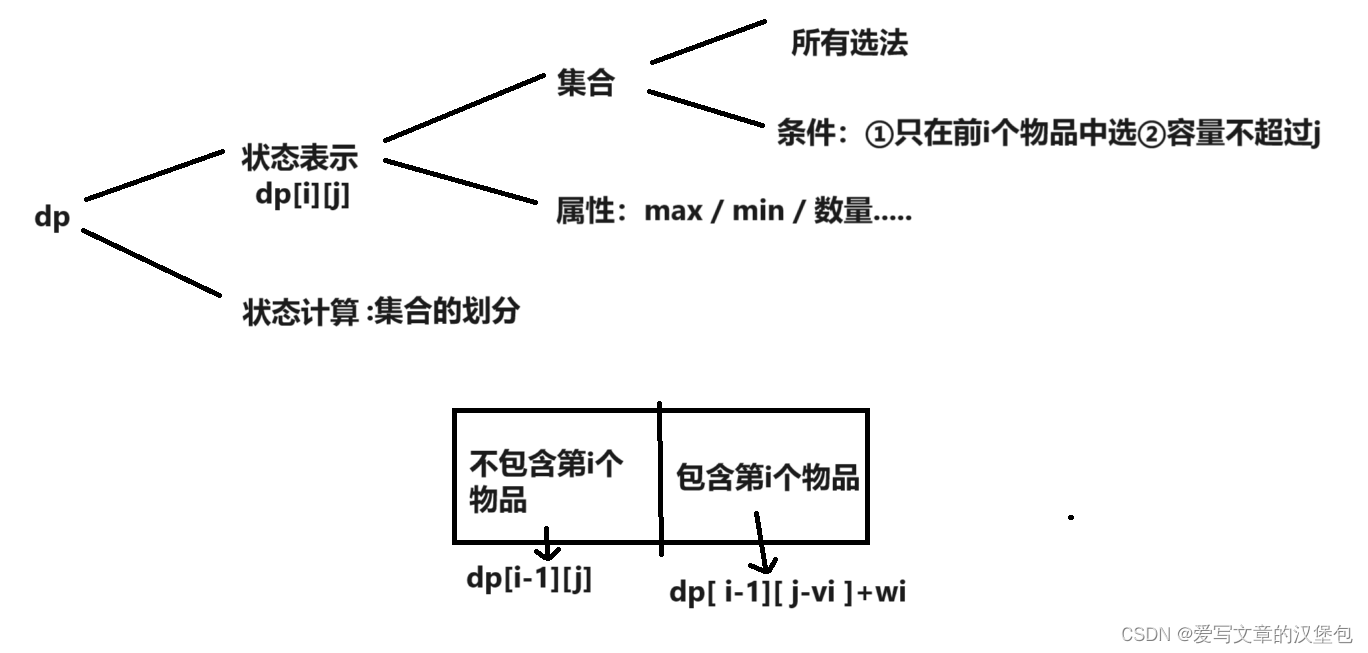
这二者几乎是一样的。
注意点
①因为根据上面的分析,我们需要用到上一次计算的结果,因此会出现二维数组下标进行-1的操作,因此我们读入数据下标从1开始,避免可能存在的数组越界问题。
②理解我们所定义的二维数组的行列表示方法。
③由于我们考虑向左下角还是右下角走的时候,运用状态转移方程,会访问到 f 数组的

这些位置,因此我们需要在初始化 f 数组时扩大初始化的范围,包含进来这些可能会访问到的点。
for(int i=0;i<=n;i++)
{
for(int j=0;j<=i+1;j++)
{
f[i][j]=-INF;
}
}我们把 f 数组都初始化为一个很大的负数是因为三角形中数据的范围包含负数,因此为了避免影响结果,我们需要将最大路径的初始值设为一个非常小的数。
④记得定义常量INF=0x3f3f3f3f,它表示一个很大的数,添上负号就表示一个很小的负数。
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N=510,INF=0x3f3f3f3f;
int n;
int a[N][N];
int f[N][N];//记录每个位置对应的:从起点到该位置的路径长度最大值
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>a[i][j];//读入三角形
}
}
//初始化每个位置路径最大值
for(int i=0;i<=n;i++)
{
for(int j=0;j<=i+1;j++)
{
f[i][j]=-INF;
}
}
f[1][1]=a[1][1];
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);//注意左上角和右上角的下标表示
}
}
int res=-INF;
for(int i=1;i<=n;i++)//枚举最后一行找到最大路径
{
res=max(res,f[n][i]);
}
cout<<res;
return 0;
}由于我们这样从上往下考虑的时候,需要注意我们上面所说的注意点③的边界问题。
但是如果我们从下往上考虑,对于每一个数,我们只需要考虑这个数是从它的左下角还是右下角走过来的,因为我们从下往上考虑,所以我们考虑的数一定是存在的。这样就避免了我们由于担心有些不合法的数而多写的一些代码。
#include<iostream>
#include<algorithm>
using namespace std;
const int N=510;
int f[N][N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>f[i][j];
}
}
for(int i=n-1;i;i--)//从底向上
{
for(int j=1;j<=n;j++)
{
f[i][j]+=max(f[i+1][j],f[i+1][j+1]);
}
}
cout<<f[1][1];
return 0;
}这样的代码是从下往上考虑的写法,并进行了优化,由于刚开始输入的三角形只会被使用一次,因此我们可以之创建一个二维数组,在其基础上直接修改。
由于我们的 i 是不断递减的,所以状态转移方程由原来的+1变成-1即可。
视频讲解推荐
【【寒假每日一题】Day-2(《898. 数字三角形》动态规划)】
这是y总的讲解,很详细也有很多知识补充。可以看看。
2020蓝桥杯省赛-数字三角形
题目链接:
数字三角形
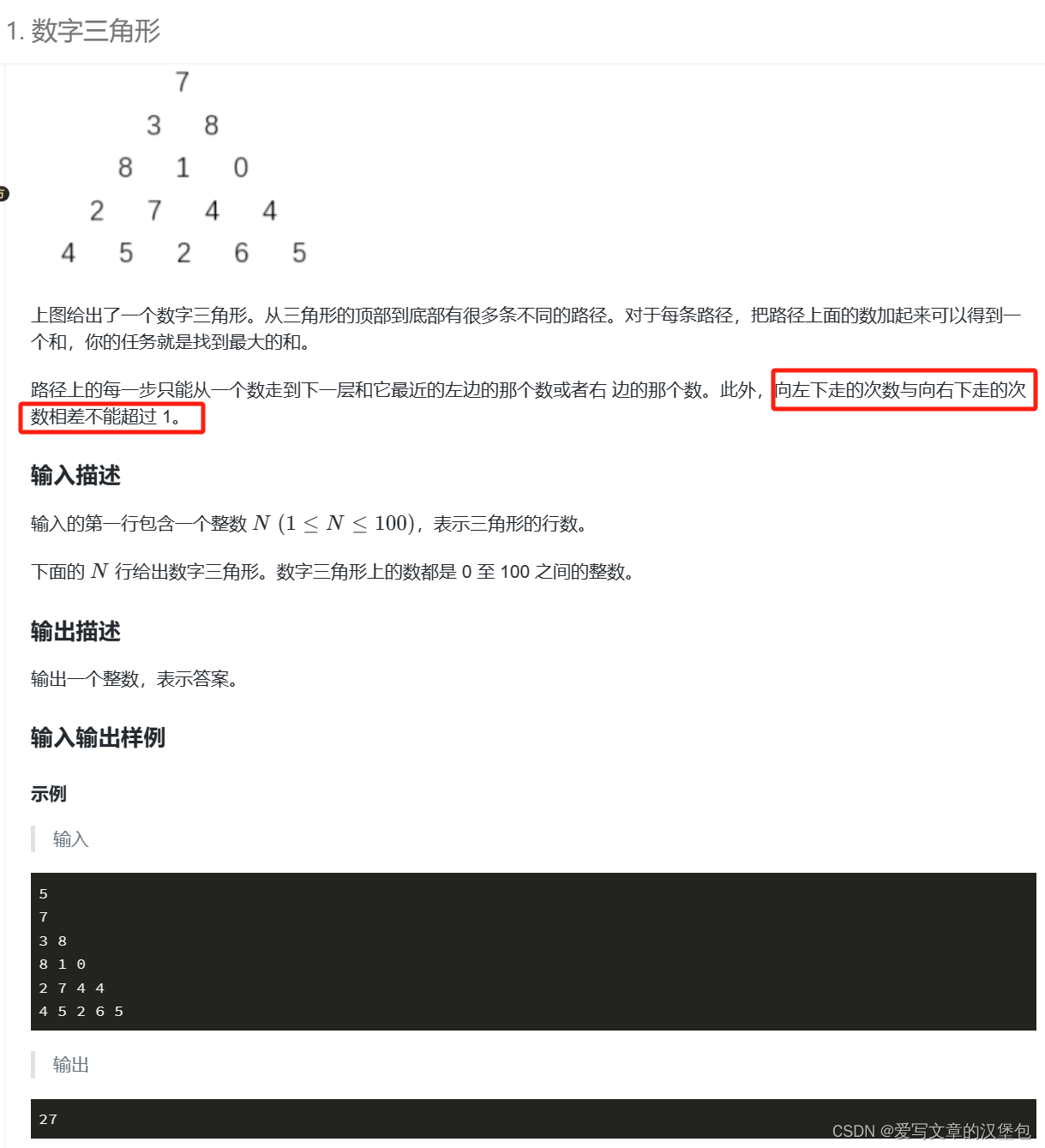
这道题和我们的模板题就多了一个条件:“向左下走的次数与向右下走的次数相差不能超过 1”
错误思路 (可不看)
我刚开始我想着他既然是要求了走两边的次数相差,那我就定义两个变量记录次数,保证我们符合题意就行。
然后写出来这个鬼东西😂👌
就把两层循环里的内容改成了这个
if(f[i-1][j-1]>f[i-1][j] || (abs(l-r)<=1 && l<r)
{
l++;
f[i][j]=a[i][j]+f[i-1][j-1];
}
else{
r++;
f[i][j]=a[i][j]+f[i-1][j];}这里我是忘记了 f 数组的含义:我们每一个 f 都是这个数所对应的可能性的最大值,我们经历循环的时候是不断地更新每个不同数字的最大值的过程,而不针对某一个数字的到达路径。
虽然这道题我们写的两层循环,但即使是内层循环也是针对所有不同的数字的,而不针对某一个数字的。
因此这样的写法思路都是错误的。
思路
我这里还是按照从上往下的思路考虑的。
由于新增的这个条件意思是我们向左和向右走的次数差不多,这个条件会导致我们的路径更倾向于走向三角形的中心。
为了获得最大的路径和,最后一行中间位置的值应该是最大的可能值。因为如果最后一行中间位置的值不是最大的可能值,而是更接近于左边或右边的值,那么要么向左下走的次数会多于向右下走的次数,要么相反,违反了给定的条件。
关于这一点我们可以画个图自己走一下试试,就明白了。
(注意这个条件并不是说我们走的时候只能是一次左边一次右边,这里不要想错了(我想错了doge)
好了,理解这个条件给出的信息之后,我们就着重看这个信息告诉我们什么?
根据满足“向左下走的次数与向右下走的次数相差不能超过 1”,我们发现可能走到最后我们得到的答案很可能处在三角形最后一层的中心位置,那么我们就要考虑到当层数是偶数时,会有两个中间值,奇数情况下只有一个确定的值。
下面是一个例子
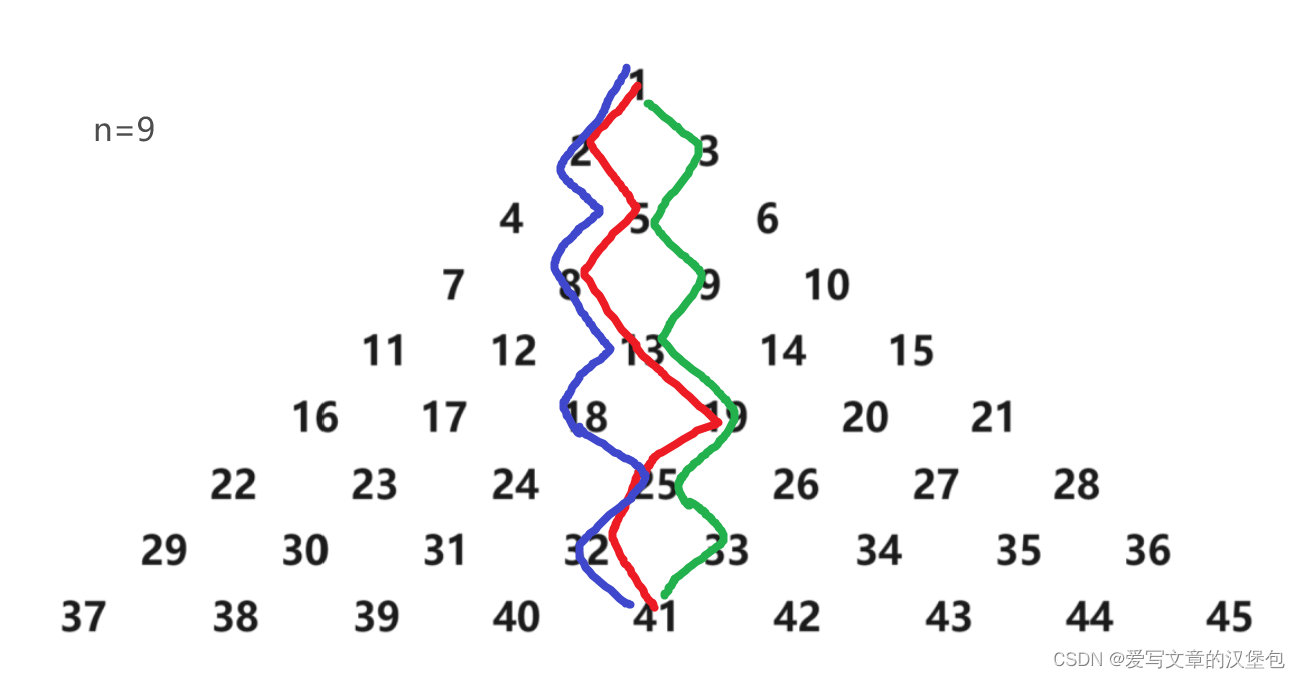
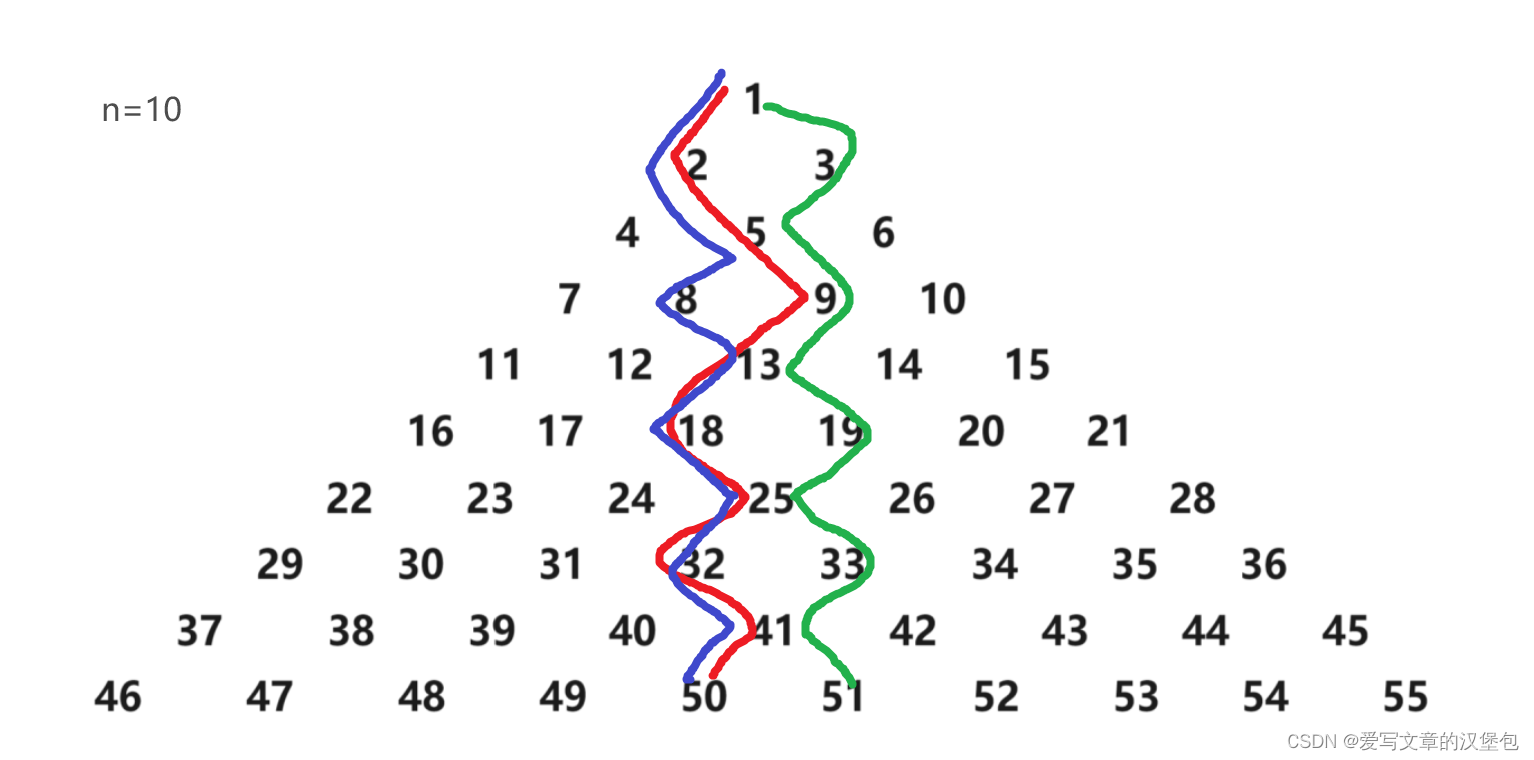
那么这道题的思路就清晰了,在我们模板的基础上 ,最后输出的时候对 n 的奇偶性进行判断,执行不同的结果就可以了。
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110,INF=0x3f3f3f3f;
int f[N][N],w[N][N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>w[i][j];
}
}
for(int i=0;i<=n;i++)//采用从上往下的思考方式一定要初始化
{
for(int j=0;j<=i+1;j++)
{
f[i][j]=-INF;
}
}
f[1][1]=w[1][1];//一定要记得赋第一个值
for(int i=2;i<=n;i++)//记得i从2开始
{
for(int j=1;j<=i;j++)
{
f[i][j]=w[i][j]+max(f[i-1][j],f[i-1][j-1]);
}
}
if(n%2)cout<<f[n][n/2+1];//奇数
else cout<<max(f[n][n/2],f[n][n/2+1]);//偶数
return 0;
}注意点
①采用从上往下的考虑方式一定要初始化 dp 数组
②记得把第一行的第一个值提前赋值f[1][1]=w[1][1]; 同时由于第一个值已经设置过,所以在下面的给dp数组赋值的双层循环中,行数 i 从2开始。这点一定要注意。
③最后分奇偶的输出结果不要搞错了,输出的是第n行的中间值。
这次先写到这里啦。
有问题欢迎指出,一起加油!!






![【Hadoop】-Apache Hive使用语法与概念原理[15]](https://img-blog.csdnimg.cn/direct/493b098a7ea94176ae87e70de30a1aca.png)