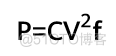84.柱状图中的最大的图形
总体思路:找到左右两个方向第一个小于该柱子高度的下标,用右下标-左下标-1得到该柱子高度对应的宽度w,再用宽度w*高度h得到面积,返回面积最大值
双指针法(超时)
for循环判断左右第一个小于高度的下标,超时
动态规划
利用minLeftIndex,minRightIndex存放第一个小于height[i]的下标值
minLeftIndex[0]初始化为-1,minRightIndex[size-1]初始化为size,防止while死循环
- 从左到右遍历
将i左边柱子t的高度与其进行比较,如果左边柱子高度大于i柱子的高度,就用minLeftIndex[t]得到第一个小于左边柱子高度的柱子下标,并将其赋值给t,再比较minLeftIndex[t]与minLeftIndex[i],直到minLeftIndex[t]小于minLeftIndex[i],终止循环,将t赋值给minLeftIndex[i]
int t = i - 1;
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
- 从右到左遍历
将i右边柱子t的高度与其进行比较,如果右边柱子高度大于i柱子的高度,就用minRightIndex[t]得到第一个小于右边柱子高度的柱子下标,并将其赋值给t,再比较minRightIndex[t]与minRightIndex[i],直到minRightIndex[t]小于minRightIndex[i],终止循环,将t赋值给minRightIndex[i]
int t = i + 1;
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
最后求对应的矩形面积
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
返回面积最大值
单调栈
** 本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序!**
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度

先向height数组的前后各加一个高度0,以能够计算所有的面积
- 情况一:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
- 情况二:当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
- 情况三:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
// 第一个元素已经入栈,从下标1开始
for (int i = 1; i < heights.size(); i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
st.push(i);
} else {
while (heights[i] < heights[st.top()]) { // 注意是while
int mid = st.top();
st.pop();
int left = st.top();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
}