JavaScript算法描述【排序与搜索】六大经典排序|合并两个有序数组|第一个错误的版本

在这里插入图片描述

🐧主页详情：Choice~的个人主页
📢作者简介：🏅物联网领域创作者🏅 and 🏅阿里专家博主🏅 and 🏅华为云享专家🏅
✍️人生格言：最慢的步伐不是跬步，而是徘徊；最快的脚步不是冲刺，而是坚持。
🧑‍💻人生目标：成为一名合格的程序员，做未完成的梦：实现财富自由。
🚩技术方向：NULL
🀄如果觉得博主的文章还不错的话，请三连支持一下博主哦

🏫系列专栏(免费)：
1️⃣ C语言进阶
2️⃣ 数据结构与算法(C语言版)
3️⃣ Linux宝典
4️⃣ C++从入门到精通
5️⃣ C++从入门到实战
6️⃣ JavaScript从入门到精通
7️⃣101算法JavaScript描述
8️⃣微信小程序零基础开发
9️⃣牛客网刷题笔记
🔟计算机行业知识(补充)

文章目录

排序与搜索
- 算法复杂度
- 冒泡排序(Bubble Sort)
- - 实现原理
  - 代码
- 选择排序(Selection Sort)
- 插入排序(Insertion Sort)
- - 希尔排序(Shell Sort)
  - 快速排序(Quick Sort)
  - 归并排序(Merge Sort)
合并两个有序数组、第一个错误的版本
- 合并两个有序数组
- - 方法一双指针从前往后遍历
  - 详解
  - 方法二双指针从后往前遍历
  - 方法三利用 array.sort()方法
- 第一个错误的版本
- - 方法一暴力法[超出时间限制]
  - 方法二二分法

排序与搜索

排序算法(sorting algorithm)是一种能将一串数据依照特定顺序进行排列的一种算法。

排序算法的一个指标是稳定性，稳定性即：如果只按照第一个数字排序的话，第一个数字相同而第二个数字不同的，第二个数字按照原有排序的就是稳定排序，不按照原有排序的就是不稳定排序。

算法复杂度

排序方法	时间复杂度(平均)	时间复杂度(最坏)	时间复杂度(最好)	空间复杂度	稳定性
冒泡排序	O(n^2)O(n2)	O(n^2)O(n2)	O(n)O(n)	O(1)O(1)	稳定
选择排序	O(n^2)O(n2)	O(n^2)O(n2)	O(n^2)O(n2)	O(1)O(1)	不稳定
插入排序	O(n^2)O(n2)	O(n^2)O(n2)	O(n)O(n)	O(1)O(1)	稳定
希尔排序	O(n^{1.3})O(n1.3)	O(n^2)O(n2)	O(n)O(n)	O(1)O(1)	不稳定
快速排序	O(nlog_2{n})O(nlog2n)	O(n^2)O(n2)	O(nlog_2{n})O(nlog2n)	O(nlog_2{n})O(nlog2n)	不稳定
归并排序	O(nlog_2{n})O(nlog2n)	O(nlog_2{n})O(nlog2n)	O(nlog_2{n})O(nlog2n)	O(n)O(n)	稳定

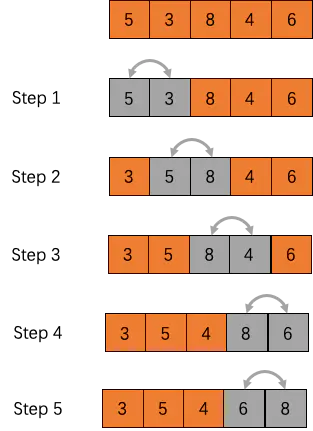
冒泡排序(Bubble Sort)

我们先来了解一下冒泡排序算法，虽然比较容易实现，但是比较慢。之所以称之为冒泡排序是因为使用这种排序算法时，像气泡一样从数组的一端冒到另一端。

实现原理

每次比较，相邻的元素，如果第一个比第二个大，就交换两个元素的位置
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

[^重复 1 - 5]:

代码

function bubbleSort(arr) {
  const len = arr.length;
  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j+1]) {
        const temp = arr[j+1];
        arr[j+1] = arr[j];
        arr[j] = temp;
      }
    }
  }
  return arr;
}

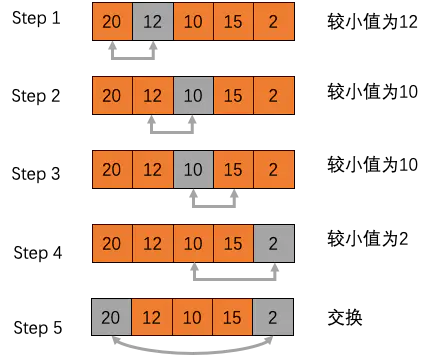
选择排序(Selection Sort)

选择排序是一种简单直观的排序算法。选择排序从数组的开头开始，将第一个元素和其他元素进行比较，检查完所有元素后最小的元素会被放到数组的第一个位置，然后从第二个元素开始继续。这个过程一直进行到数组的倒数第二个位置。

function selectionSort(arr) {
  const len = arr.length;
  let minIndex;
  let temp;
  for (let i = 0; i < len - 1; i++) {
      minIndex = i;
      for (let j = i + 1; j < len; j++) {
        if (arr[j] < arr[minIndex]) { 
          minIndex = j; // 保存最小数的索引
        }
      }
      temp = arr[i];
      arr[i] = arr[minIndex];
      arr[minIndex] = temp;
  }
  return arr;
}

插入排序(Insertion Sort)

插入排序类似于按首字母或者数字对数据进行排序。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

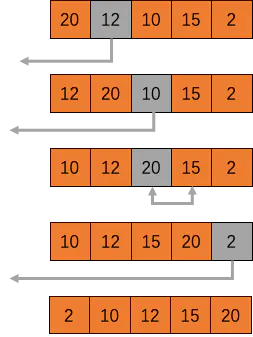
function insertionSort(arr) {
  const len = arr.length;
  let preIndex;
  let current;
  for (let i = 1; i < len; i++) {
    preIndex = i - 1;
    current = arr[i];
    // 大于新元素，将该元素移到下一位置
    while (preIndex >= 0 && arr[preIndex] > current) {
      arr[preIndex + 1] = arr[preIndex];
      preIndex--;
    }
    arr[preIndex + 1] = current;
  }
  return arr;
}

希尔排序(Shell Sort)

希尔排序之所以叫希尔排序，因为它就希老爷子(Donald Shell)创造的。希尔排序对插入做了很大的改善。核心理念与插入排序的不同之处在于，它会优先比较距离较远的元素，而不是相邻的元素。当开始用这个算法遍历数据集时，所有元素之间的距离会不断减少，直到处理到数据的末尾。

function shellSort(arr) {
  const len = arr.length;
  let gap = Math.floor(len / 2);

  while (gap > 0) {
    for (let i = gap; i < len; i++) {
      const temp = arr[i];

      let j = i;
      while (j >= gap && arr[j - gap] > temp) {
        arr[j] = arr[j - gap];
        j -= gap;
      }
      arr[j] = temp;
    }
    gap = Math.floor(gap / 2);
  }
  return arr;
}

快速排序(Quick Sort)

快速排序一般用来处理大数据集，速度比较快。快速排序通过递归的方式，将数据依次分为包含较小元素和较大元素的不同子序列。

实现原理

这个算法首先要在列表中选择一个元素作为基准值，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面。这个基准值一般有 4 种取法：

无脑拿第一个元素
无脑拿最后一个元素
无脑拿中间的元素
随便拿一个

下面的解法基于取最后一个元素实现：

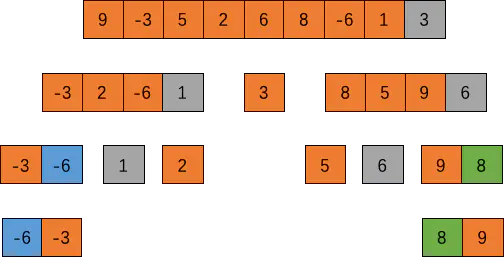
function partition(arr, low, high) {
  let i = low - 1; // 较小元素的索引
  const pivot = arr[high];

  for (let j = low; j < high; j++) {
    // 当前的值比 pivot 小
    if (arr[j] < pivot) {
      i++;
      [arr[i], arr[j]] = [arr[j], arr[i]] 
    }
  }
  [arr[i + 1], arr[high]] = [arr[high], arr[i + 1]]
  return i + 1;
}

function quickSort(arr, low, high) {
  if (low < high) {
    const pi = partition(arr, low, high) 
    quickSort(arr, low, pi - 1) 
    quickSort(arr, pi + 1, high) 
  }
  return arr;
}

归并排序(Merge Sort)

归并排序是把一系列排好序的子序列合并成一个大的完整有序序列。

实现原理

把长度为 n 的输入序列分成两个长度为 n / 2 的子序列，载对这两个子序列分别采用归并排序，最后将两个排序好的子序列合并成一个最终的排序序列。

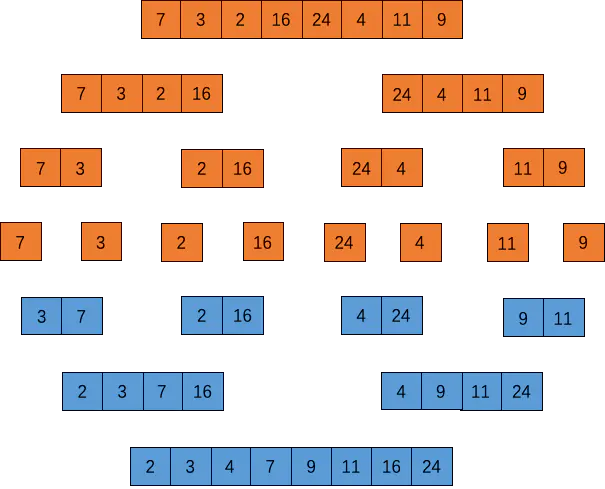
代码

function mergeSort(arr) {
  const len = arr.length;
  if (arr.length > 1) {
    const mid = Math.floor(len / 2); // 对半分
    const L = arr.slice(0, mid);
    const R = arr.slice(mid, len);

    let i = 0;
    let j = 0;
    let k = 0;

    mergeSort(L); // 对左边的进行排序
    mergeSort(R); // 对右边的进行排序

    while (i < L.length && j < R.length) {
      if (L[i] < R[j]) {
        arr[k] = L[i];
        i++;
      } else {
        arr[k] = R[j];
        j++
      }
      k++;
    }

    // 检查是否有剩余项
    while (i < L.length) {
      arr[k] = L[i];
      i++;
      k++;
    }

    while (j < R.length) {
      arr[k] = R[j];
      j++;
      k++;
    }
  }
  return arr;
}

本章节将分为 3 个部分：

Part 1
- 合并两个有序数组 🌟
- 第一个错误的版本 🌟
- 搜索旋转排序数组 🌟🌟
Part 2
- 在排序数组中查找元素的第一个和最后一个位置 🌟🌟
- 数组中的第K个最大元素 🌟🌟
- 颜色分类 🌟🌟
Part 3
- 前K个高频元素 🌟🌟
- 寻找峰值 🌟🌟
- 合并区间 🌟🌟
Part 4
- 搜索二维矩阵 || 🌟🌟
- 计算右侧小于当前元素的个数 🌟🌟

合并两个有序数组、第一个错误的版本

合并两个有序数组

给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。

说明:

初始化 nums1 和 nums2 的元素数量分别为 m 和 n。你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。

示例

输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

方法一双指针从前往后遍历

思路

先简化问题，从合并数组简化成合并两个元素。分别从两个数组中取出一个元素进行比较，比较完后将较小元素合并进结果数组，较大元素继续和另一个数组中取的下一个元素比较，如此循环，直到某个数组中的元素都被比较过时，剩下的数组中未被比较过的元素直接按顺序放到结果数组中。

详解

定义两个指针 j、k，分别指向当前 nums1 与 nums2 数组中第一个元素的下标，定义一个 result 数组存放合并结果
比较 nums1[j] 和 nums2[k] 两个元素，将较小元素 push 进 result 中
1. 指向较小元素的指针加 1，取出上次较大元素继续比较，循环第 2 步
2. 当某个数组中的元素都被比较过了，将另一数组剩余元素直接 push 到 result 中，因为两个数组都是有序数组，剩下的肯定是较大值

代码

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void}
 */
const merge = function (nums1, m, nums2, n) {
  // 暂存 merge 结果
  const result = [];
  // 定义两个指针 j、k，分别指向当前 nums1 与 nums2 数组中正在比较值的数组下标，从前往后
  let j = 0; let k = 0;
  // 遍历 nums1 和 nums2 数组，遍历完一个数组后跳出循环
  while (j < m && k < n) {
    // 比较 nums1 中取的值与 nums2 中取的值，将较小值 push 到结果数组中
    // 并将下标往后加一，下次循环取后一个值进行比较
    if (nums1[j] > nums2[k]) {
      result.push(nums2[k]);
      k++;
    } else {
      result.push(nums1[j]);
      j++;
    }
  }

  // nums1 或 nums2 中有一个数组未遍历完全
  if (result.length < m + n) {
    // 如果 nums1 遍历完了，则说明 nums2 未遍历完全，
    // 将 nums2 中剩余未比较的数据直接 push 到 merge 结果数组中
    // 反之亦然
    if (j === m) {
      result.push(...nums2.slice(k, n));
    } else {
      result.push(...nums1.slice(j, m));
    }
  }
  // 清空 nums1，将 merge 结果 push 到 nums1 中
  nums1.splice(0, nums1.length);
  nums1.push(...result);
};

复杂度分析

时间复杂度： O(m + n)O(m+n)

最多遍历 m + n -1m+n−1 次，所以时间复杂度为 O(m + n)O(m+n)
空间复杂度：O(m)O(m)

开辟新的空间存放 nums1 数组，所以空间复杂度为 O(m)O(m)

方法二双指针从后往前遍历

思路

先简化问题，从合并数组简化成合并两个元素。因为 nums1 数组长度可以存放最后排序好的元素，所以可以从后往前取两个数组的元素进行比较，从 nums1 数组的最后开始存放较大元素。较小值继续与新取出的元素进行比较，如此循环直到某个数组中的元素全部被比较过，可得最终结果。

详解

1.定义一个指针 p，指向 nums1 数组最后一个位置(m + n - 1)。 2.比较 nums1[m - 1] 和 nums2[n - 1] 两个元素，将较大元素放到 nums1[p] 中 3.指针 p 往前移动一位，，较大元素所在数组往前继续取出一个元素与上次较小元素进行比较，将较大元素放到 nums1[p] 中 4.循环第 3 步，直到某个数组中的元素全部被比较过，因为 nums1 和 nums2 数组都是有序数组，所以另一数组未比较的元素肯定是较小的那部分元素，直接将剩余元素放到 nums1 的头部

代码

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void}
 */
const merge = function (nums1, m, nums2, n) {
  let currentInsertIndex = nums1.length - 1;
  while (currentInsertIndex >= 0 && n > 0 && m > 0) {
    if (nums1[m - 1] > nums2[n - 1]) {
      nums1[currentInsertIndex--] = nums1[m - 1];
      m--;
    } else {
      nums1[currentInsertIndex--] = nums2[n - 1];
      n--;
    }
  }

  // nums2 未遍历完成，将 nums2 中剩余未遍历的数据插入到 nums1 头部
  // nums1 未遍历完成不用关心，已排序好了
  if (n > 0) {
    nums1.splice(0, n, ...nums2.slice(0, n));
  }
};

复杂度分析

时间复杂度：O(m + n)O(m+n)

最多遍历 m + n - 1m+n−1 次，所以时间复杂度为 O(m + n)O(m+n)
空间复杂度： O(1)O(1)

不需要开辟新的空间，所以空间复杂度为 O(1)O(1)

方法三利用 array.sort()方法

思路

直接合并两个数组并排序

详解

1.将 nums1 后面的占位删除并将 nums2 合并 2.用 array.sort() 方法排序

代码

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void}
 */
const merge = function (nums1, m, nums2, n) {
  // 两数组合并，将 nums1 后面的占位删除并放入 nums2
  nums1.splice(m, n, ...nums2);
  // 排序
  nums1.sort((a, b) => a - b);
};

复杂度分析

时间复杂度：O(nlogn)O(nlogn)

排序在 v8 引擎下的平均时间复杂度为 O(nlogn)O(nlogn)
空间复杂度：O(nlogn)O(nlogn)

排序在 v8 引擎下的平均空间复杂度为 O(nlogn)O(nlogn)

第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例

给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。

方法一暴力法[超出时间限制]

思路

直接for循环找第一个错误版本。

代码

const solution = function(isBadVersion) {
  return function firstBadVersion (n) {
    for (let i = 1; i < n; i++) {
      if (isBadVersion(i)) {
        return i;
      }
    }
    return n;
  }
};

复杂度分析

时间复杂度：O(n)O(n)

该方法需要遍历每一个元素，需要耗费O(n)O(n)时间，当遇见版本特别多的时候O(n)的时间，因此改方法时间复杂度为O(n)O(n)。
空间复杂度：O(1)O(1)

该方法没有申请额外的空间，所以空间复杂度为O(1)O(1)

方法二二分法

思路

前一种方法需要遍历每一个元素，这样如果元素特别多的时候会耗时过多，这个时候通过二分法也就是折半法(有序数组中查找特定元素的搜索算法)来查找元素。

二分法思路：

首先，从数组的中间元素开始搜索，如果该元素正好是目标元素，则搜索过程结束，否则执行下一步。
如果目标元素大于/小于中间元素，则在数组大于/小于中间元素的那一半区域查找，然后重复步骤（1）的操作。
如果某一步数组为空，则表示找不到目标元素。

这样可以避免无差别遍历降低遍历耗时。

详解

确定数组左边边界值和右边边界值，找到边界值的中间值
比较中间值是否是错误版本，如果是则右边边界值=中间值-1，再找中间值比较。如果不是错误版本则左侧边界值=中间值+1，再找左侧值和右侧值之间的中间值比较，这样重复下去
当左侧边界值>右侧边界值得时候，说明右侧已经全是错误版本了，当前左侧的值就是临界值

代码

const solution = function(isBadVersion) {
  return function firstBadVersion (n) {
    let left = 1;
    let right = n;
    while (left <= right) {
      const mid = Math.floor(left + (right - left) / 2);
      if (isBadVersion(mid)) {
        right = mid - 1;
      } else {
        left = mid + 1;
      }
    }
    return left;
  }
}

复杂度分析

时间复杂度为: O(\log_2(n))O(log2(n))

对于n个元素的情况(去掉常数)

第一次二分：n/2n/2

第二次二分：n/2^2= n/4n/22=n/4、…

m次二分：n/(2^m)n/(2m)

在最坏情况下是在排除到只剩下最后一个值之后得到结果，所以为n/(2^m)n/(2m)=1，得到 2^m=n2m=n

所以时间复杂度为：O(\log_2(n))O(log2(n))
空间复杂度：O(1)O(1) 该方法没有申请额外的空间，所以空间复杂度为O(1)O(1)
如果对大家有帮助，请三连支持一下！
有问题欢迎评论区留言，及时帮大家解决！