理解归并排序的两种方法(超详细)

news2024/11/24 6:28:04

目录

前言

一.方法一：归并排序

1.1 归并思路

1.1.1 递归(分解)

1.1.2 区间(排序)

1.1.3 合并拷贝回原数组(合并)

二.归并排序过程

2.1 递归(分解)图解

2.2 归并有序区间(排序)图解

2.2.1 单独一趟排序

2.2.2 有序区间递归排序

 2.2.3 数组拷贝(合并)

2.3 归并全部代码

三.方法二：归并排序(非递归)

3.1 归并思路(非递归)

3.1.1 使用gap分割

3.1.2 比较合并

3.1.3 拷贝回原数组

3.2 归并过程(非递归)

3.2.1 多趟gap

3.2.2 合并过程

 3.3.3 归并(非递归)全部代码

前言

结合图文剖析归并排序的思路；学习分治法、递归思想、gap调整区间优化。

  1. 分治法（Divide and Conquer）：归并排序是一种分治算法，它将问题分解成多个小问题，解决这些小问题，然后将它们的解决方案组合起来解决原始问题。

  2. 递归（Recursion）：归并排序的实现通常依赖于递归，这是一种在函数内部调用自身的方法。递归是解决某些问题（如树的遍历、排序等）的强大工具。

  3. 稳定性（Stability）：归并排序是一种稳定的排序算法，这意味着相等的元素在排序后保持它们原始的相对顺序。这对于某些应用场景非常重要。

  4. 时间复杂度（Time Complexity）：归并排序的最坏、平均和最佳时间复杂度都是 O(nlog⁡n)O(nlogn)，这使得它在大多数情况下都表现良好。

  5. 空间复杂度（Space Complexity）：归并排序需要 O(n)O(n) 的额外空间来存储合并过程中的临时数组，这可能限制了它在空间受限的环境中的使用。

  6. 算法效率（Algorithm Efficiency）：通过学习归并排序，您可以更好地理解不同排序算法的效率和适用场景。

  7. 代码实现：您将学会如何实现一个有效的归并排序算法，包括如何合并两个已排序的数组以及如何递归地分解和排序数组。

  8. 调试技巧（Debugging Skills）：在实现归并排序的过程中，您可能会遇到数组越界、栈溢出等错误，学习如何解决这些问题可以提高您的调试技能。

  9. 内存管理（Memory Management）：在非递归版本的归并排序中，您需要手动管理内存，包括分配和释放，这有助于您理解程序的内存使用情况。

  10. 优化（Optimization）：了解如何优化归并排序，比如在小数组中使用插入排序以减少递归调用的开销。

  11. 算法适用性（Algorithm Applicability）：知道何时使用归并排序是合适的，例如在大数据集排序或者需要稳定排序的场合。

  12. 并行计算（Parallel Computing）：归并排序可以很容易地并行化，因为它的分治结构天然适合多线程或多处理器系统。

一.方法一：归并排序

1.1 归并思路

1.1.1 递归(分解)

1.先递归(分解)，把问题分为子问题，

1.1.2 区间(排序)

2.把数组分割为不同区间（子问题）进行两区间排序

1.1.3 合并拷贝回原数组(合并)

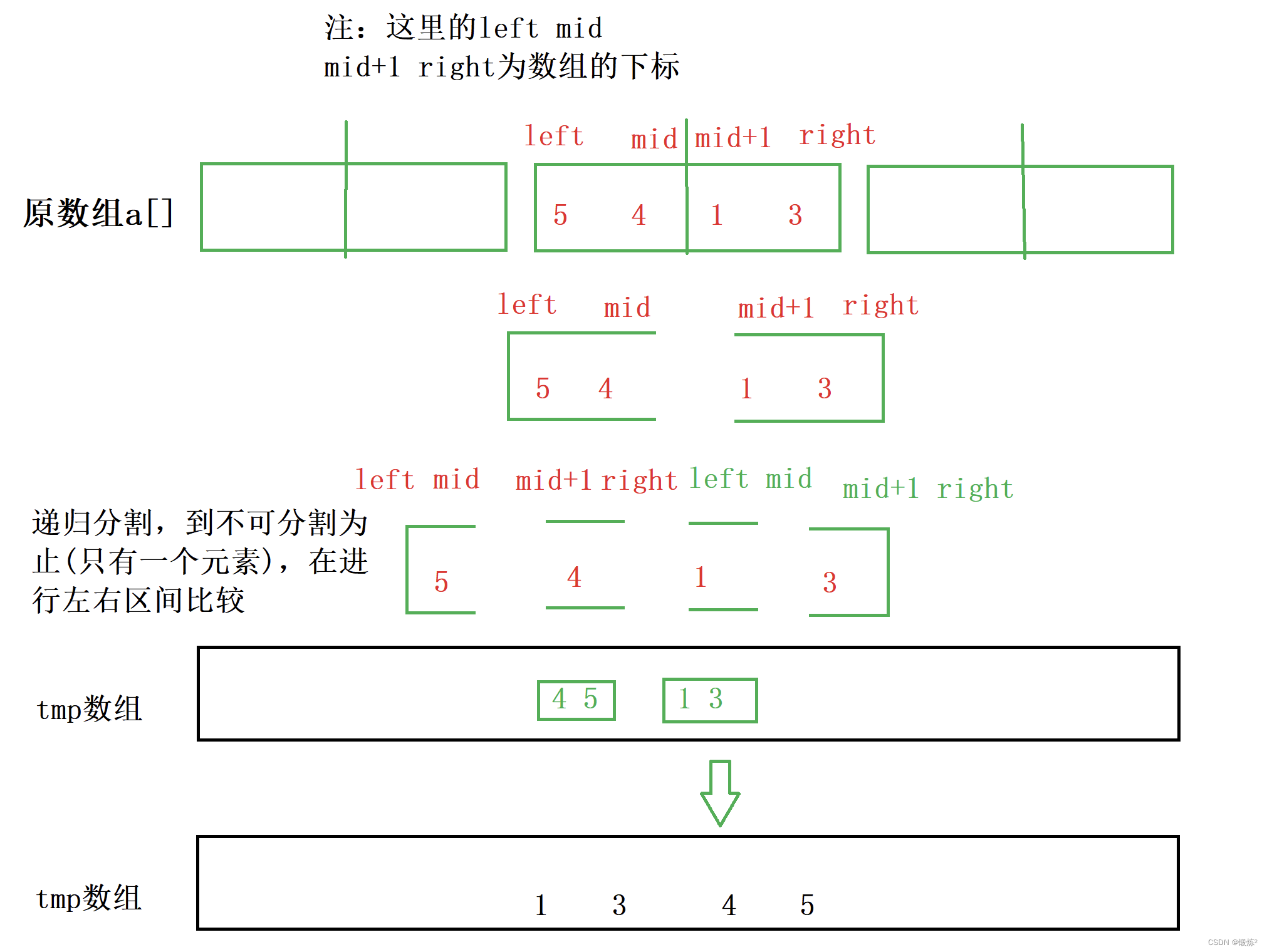
把左右区间进行排序。注意：排序过程为：比较左右区间，排序好的先放入临时数组tmp中，再把数组tmp中的内容拷贝到原数组a中

二.归并排序过程

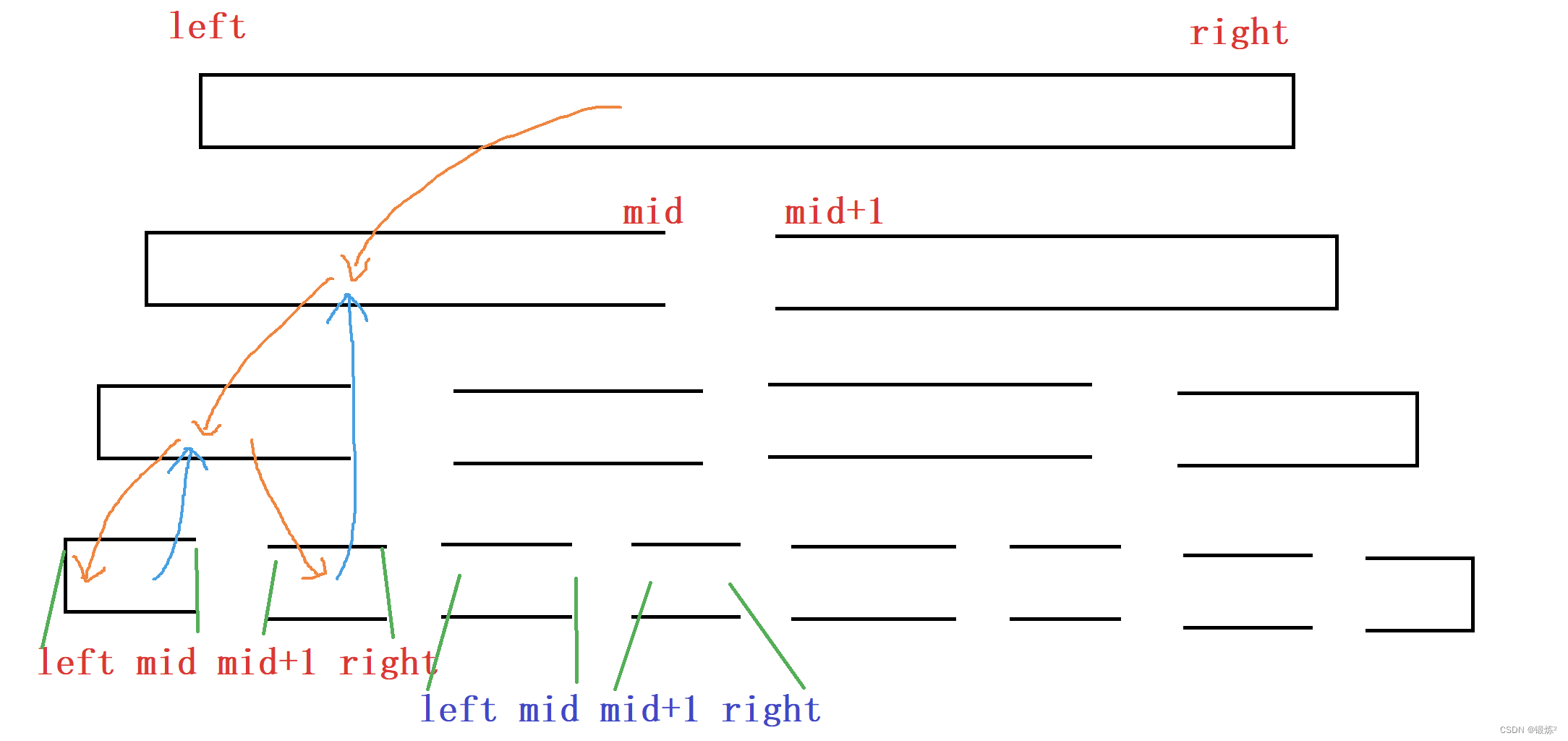
2.1 递归(分解)图解

//递归到最低层
	if (left >= right)
		return;
	//[left,mid][mid+1,right]有序，则可以合并，现在无序，子问题解决
	int mid = (left + right) / 2;
	MergeSort(a, left, mid, tmp);
	MergeSort(a, mid + 1, right, tmp);

递归过程如下：

如上图中的left mid ,当left>=right 时(left左区间大于或等于right右区间，也就是递归分解到个元素)；此时我们分解已经为个元素了，接下来要做的事情是：归并[left,mid][mid+1,right]有序

2.2 归并有序区间(排序)图解

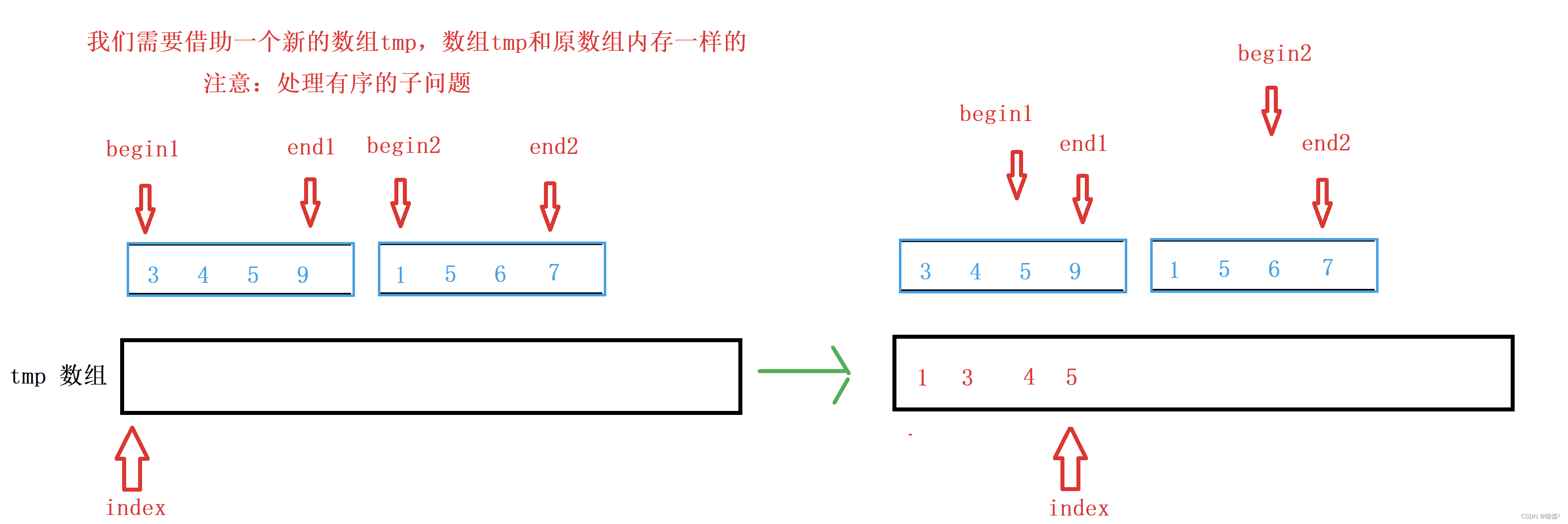
2.2.1 单独一趟排序
	//归并[left,mid][mid+1,right]有序
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}
	

	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];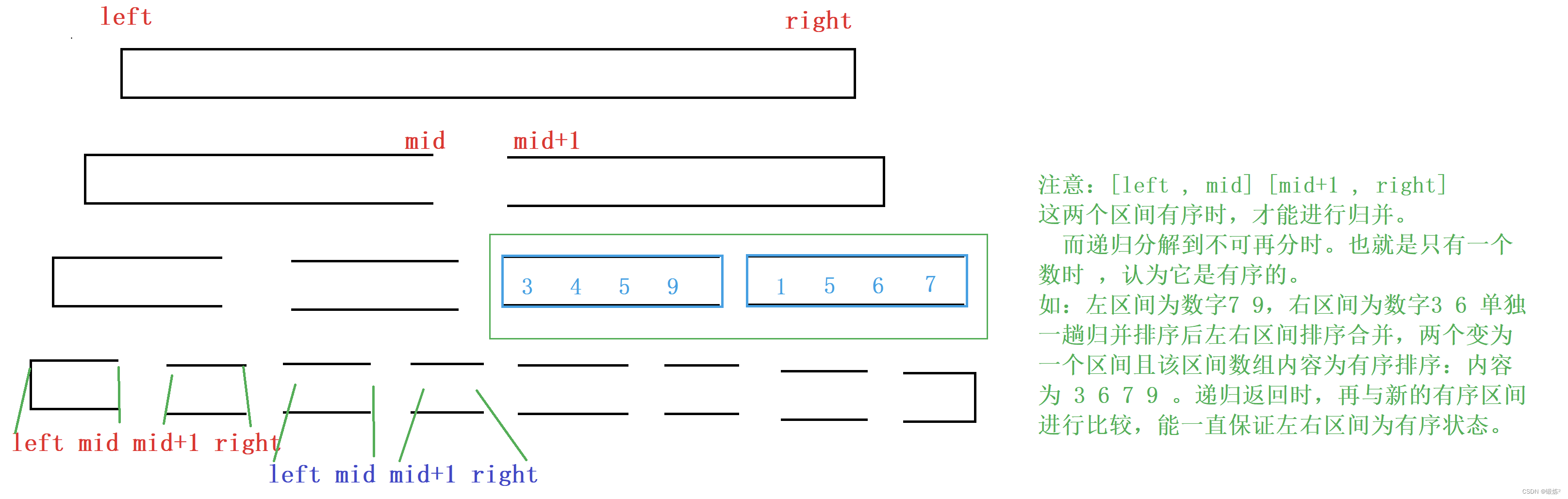
	}

​编辑

注意：[left , mid] [mid+1 , right]
这两个区间有序时，才能进行归并。
        而递归分解到不可再分时。也就是只有一个数时 ，认为它是有序的。
如：左区间为数字7 9，右区间为数字3 6 单独一趟归并排序后左右区间排序合并，2个区间变为1个区间且该合并后的区间数组内容为有序的，内容为 3 6 7 9 。递归返回时，该区间再与新的有序区间进行比较，能一直保证左右区间为有序状态，即满足归并排序的要求。

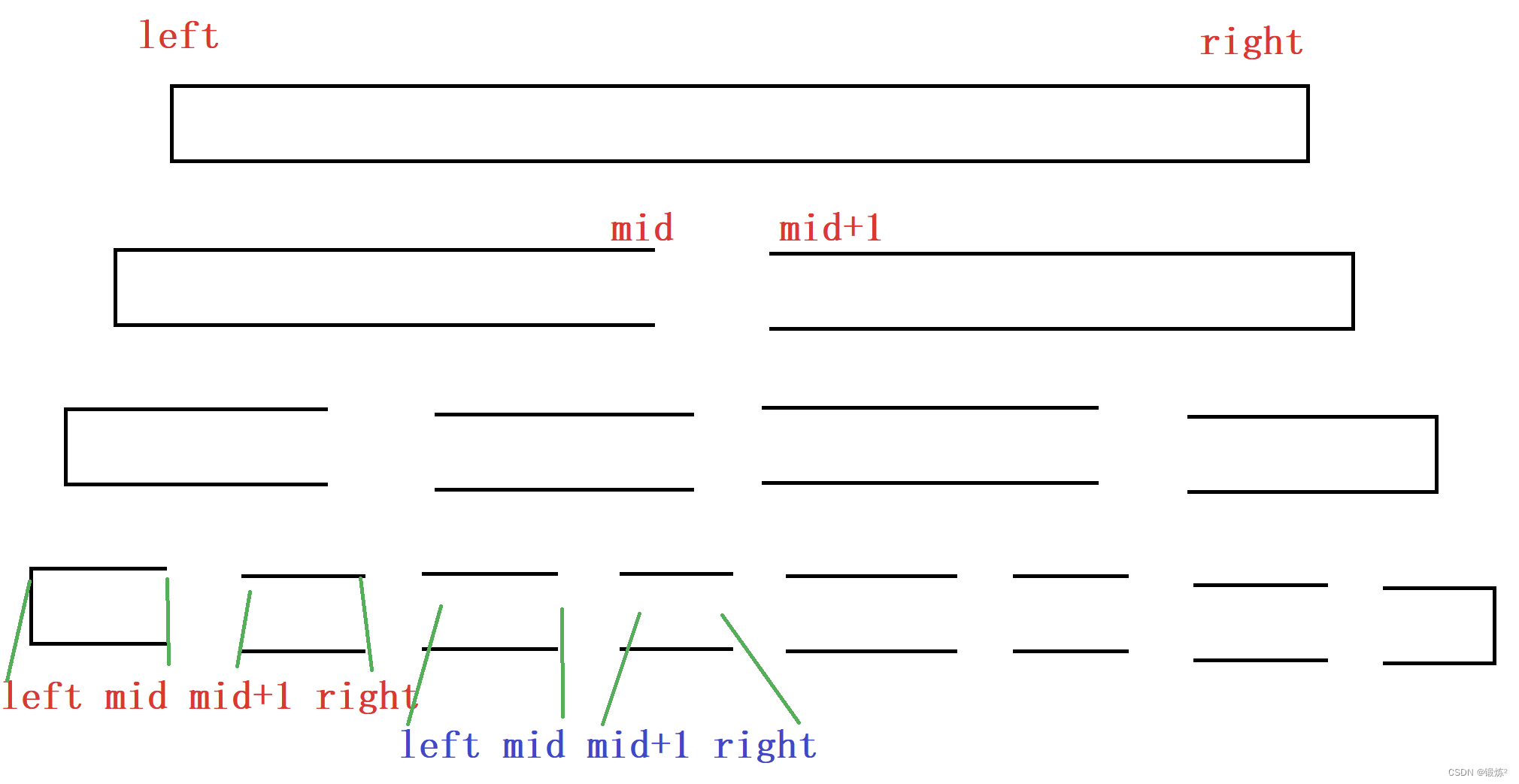
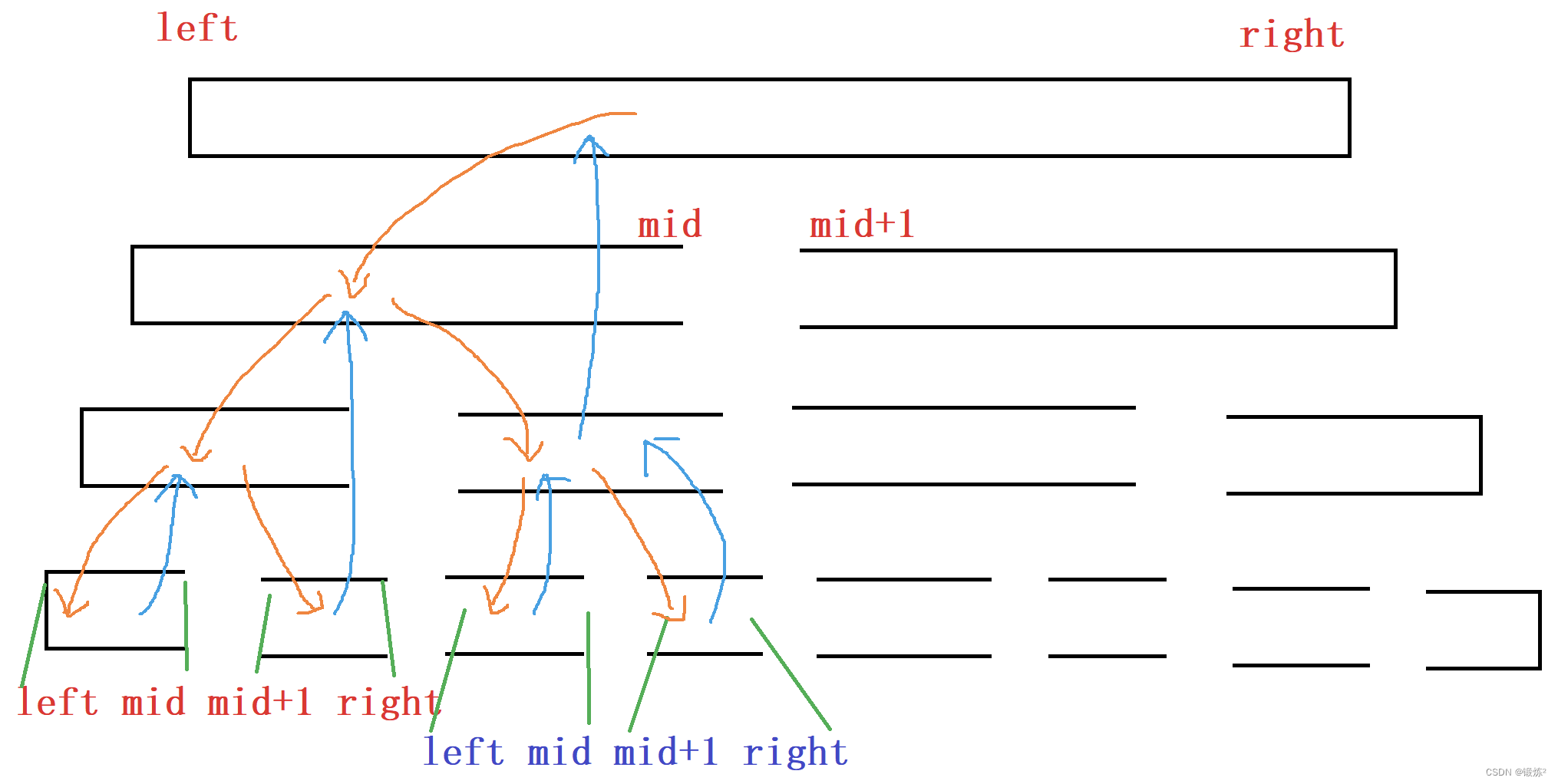
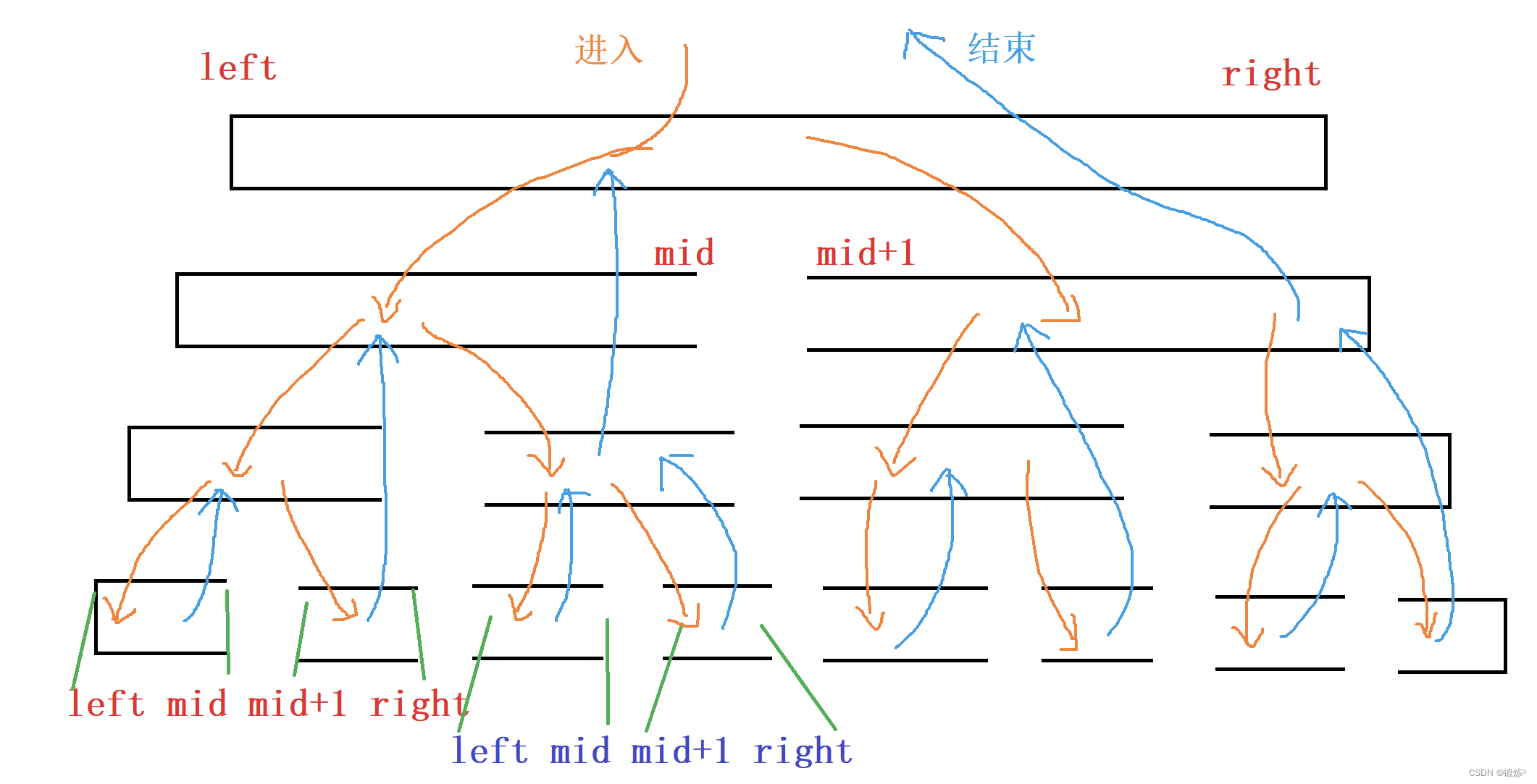
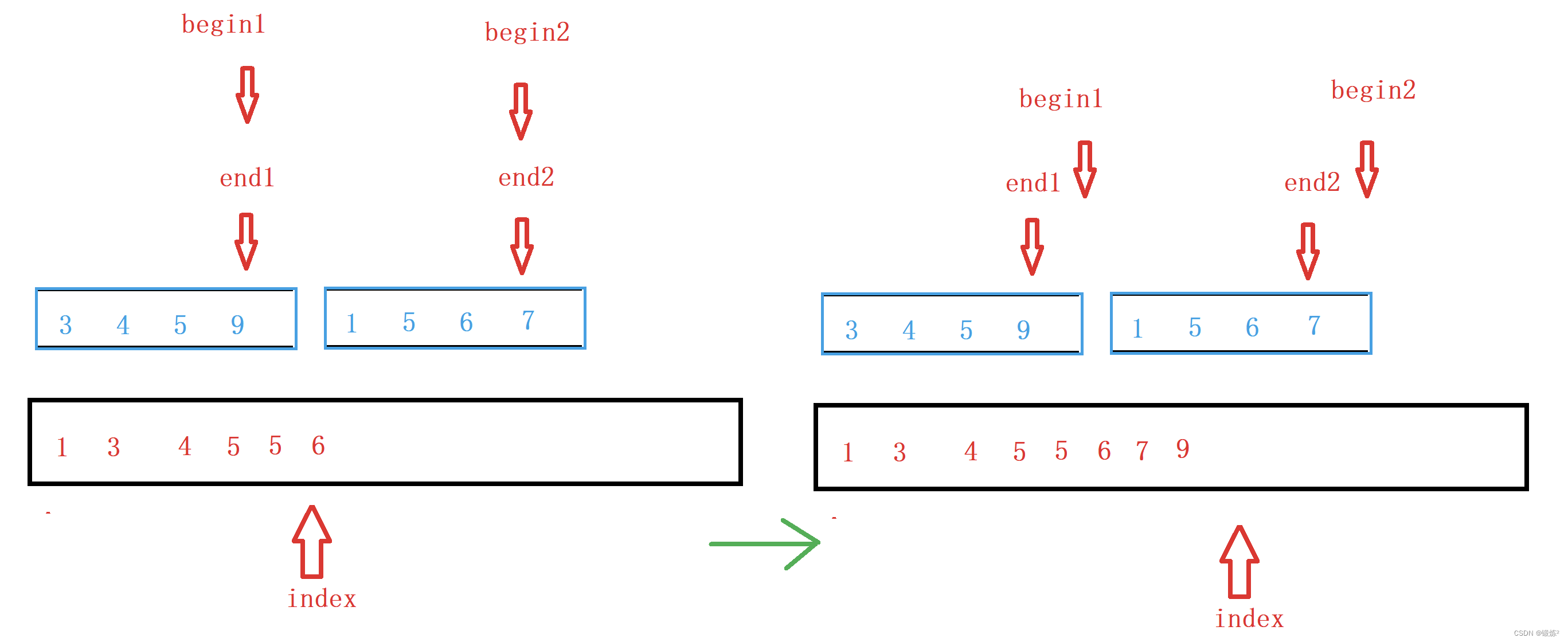
2.2.2 有序区间递归排序

那么递归排序(前面是单趟排序，这里是多趟排序)中，子问题解决后，递归返回

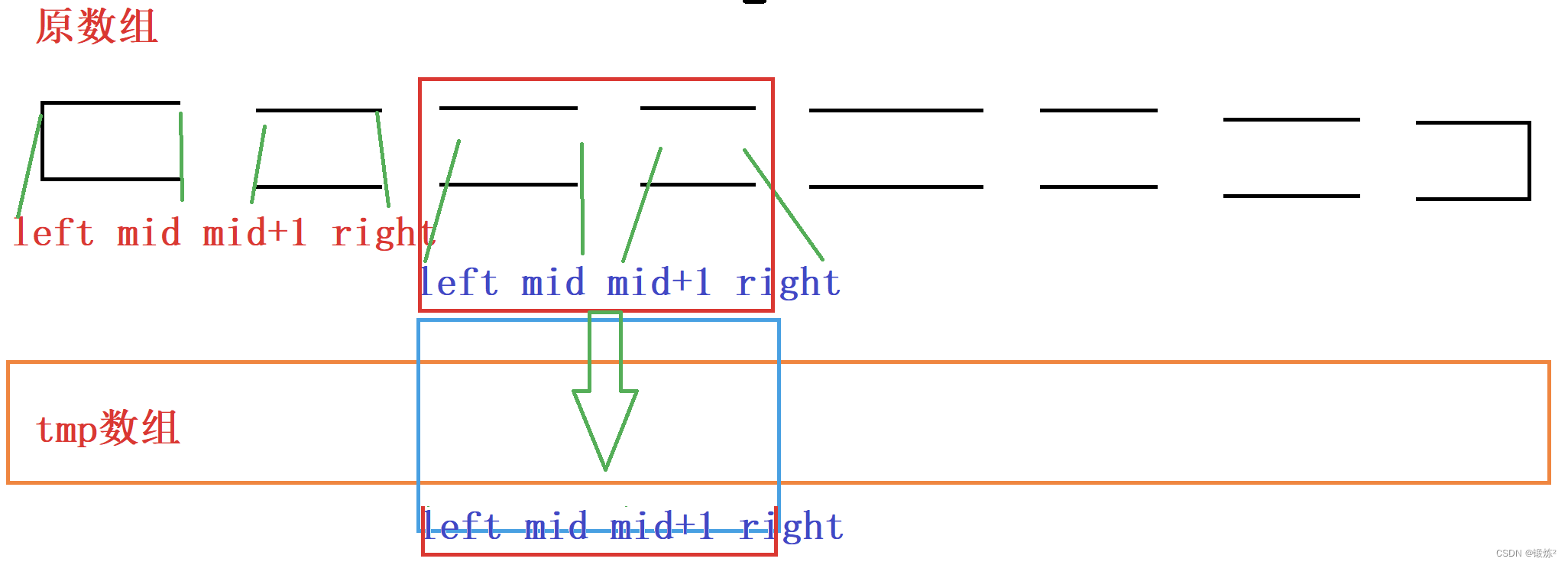
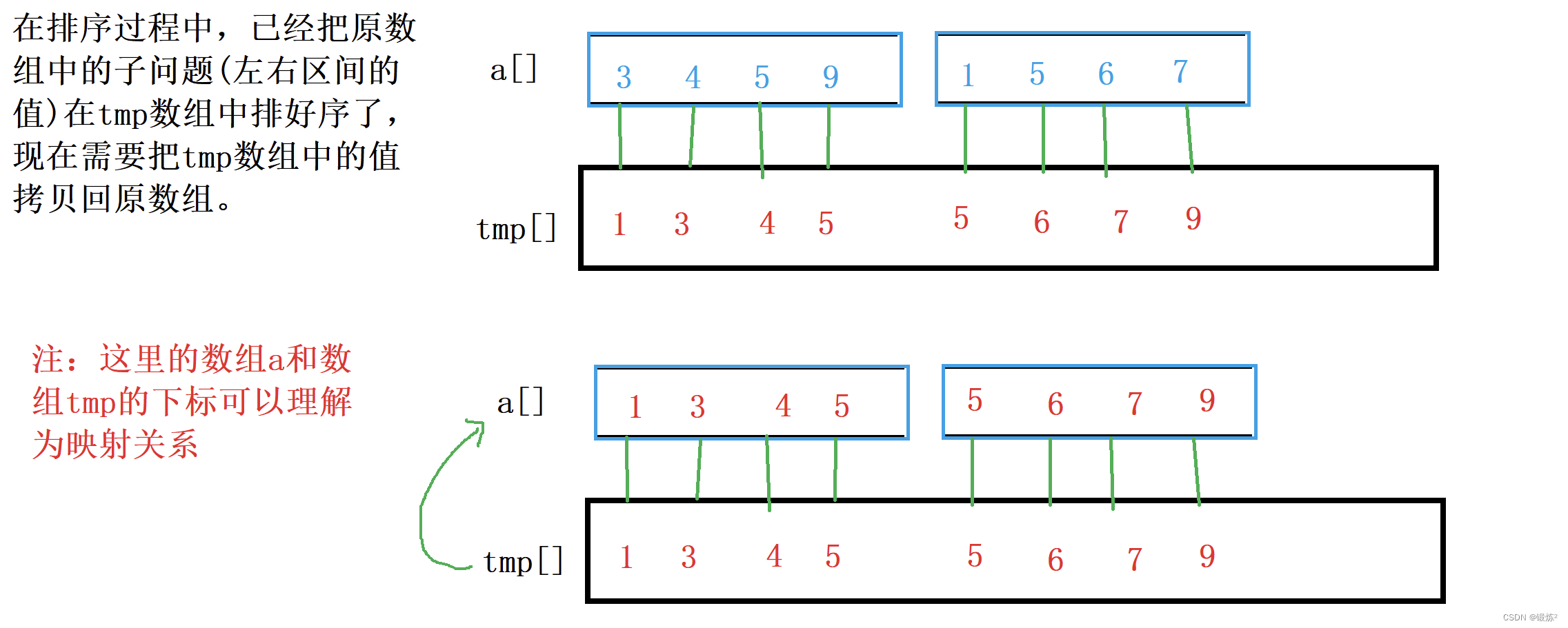
 2.2.3 数组拷贝(合并)
	//把数组tmp中的数据拷贝到原数组a中
	for (int i = left; i <= right; i++)
	{
		a[i] = tmp[i];
	}

这里合并拷贝完，接着就会返回上一层调用。也就是接着处理上一层、左右区间排序好的、数据更多的有序子问题

2.3 归并全部代码

归并排序，采用分治法，这里的归并排序通过(分解、排序、合并)，不断解决子问题：进行排序也就是归并排序

void PrintfArr(int*a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}


void MergeSort(int*a, int left, int right, int*tmp)
{
	//递归到最低层
	if (left >= right)
		return;
	//[left,mid][mid+1,right]有序，则可以合并，现在无序，子问题解决
	int mid = (left + right) / 2;
	MergeSort(a, left, mid, tmp);
	MergeSort(a, mid + 1, right, tmp);


	//归并[left,mid][mid+1,right]有序
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;

	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}
	

	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}

	//把数组tmp中的数据拷贝到原数组a中
	for (int i = left; i <= right; i++)
	{
		a[i] = tmp[i];
	}
}

void TestMergeSort()
{
	int a[] = { 3,4,2,1,5,7,8,9,4,67,2,4,9,0,10 };
	PrintfArr(a, sizeof(a) / sizeof(a[0]));
	int* tmp = (int*)malloc(sizeof(int) * (sizeof(a) / sizeof(a[0])));

	MergeSort(a, 0, sizeof(a) / sizeof(a[0])-1, tmp);
	PrintfArr(a, sizeof(a) / sizeof(a[0]));
	
	
}
int main()
{
	TestMergeSort();
	return 0;
}

三.方法二：归并排序(非递归)

3.1 归并思路(非递归)

3.1.1 使用gap分割

使用gap进行数组的分割处理，

3.1.2 比较合并

这里需要注意

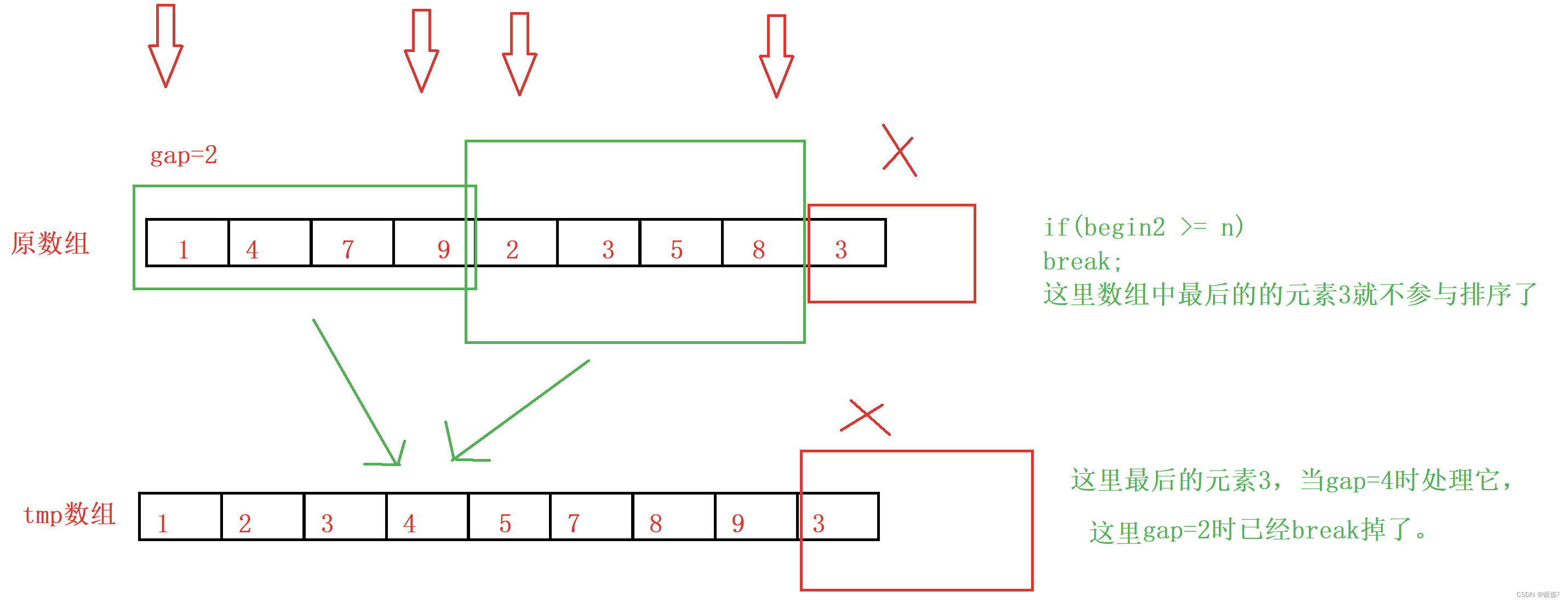
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//[i, i + gap -1][i + gap, i + 2*gap - 1]
			//修正区间 1.只有一组：
			if (begin2 >= n)
			{
				break;
			}
			//修正区间 2.有两组：右边组没满
			if (end2 >= n)
			{
				end2 = n - 1;
			}

情况一：只有左边一组(begin2到end2没数据)不需要合并，使用break跳过

这里就不对数组中最后的元素3进行合并了，等到后面gap扩大再处理。

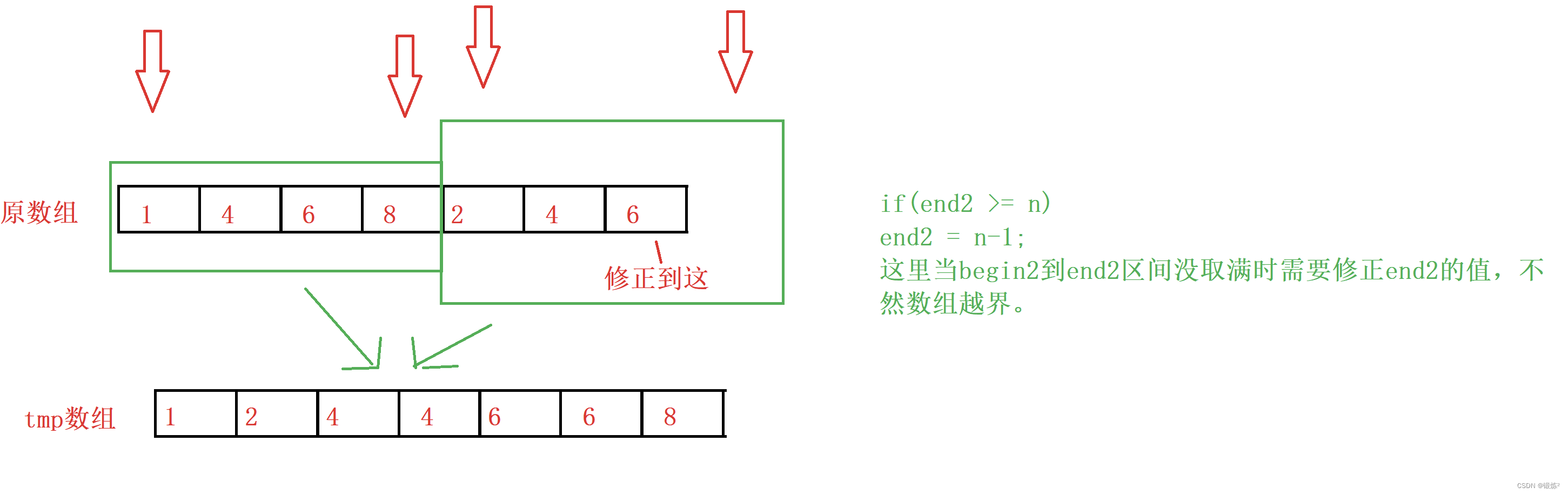
情况二：含两组数据[i, i + gap -1][i + gap, i + 2*gap - 1]但是右边区间数据没放满，需要修正区间

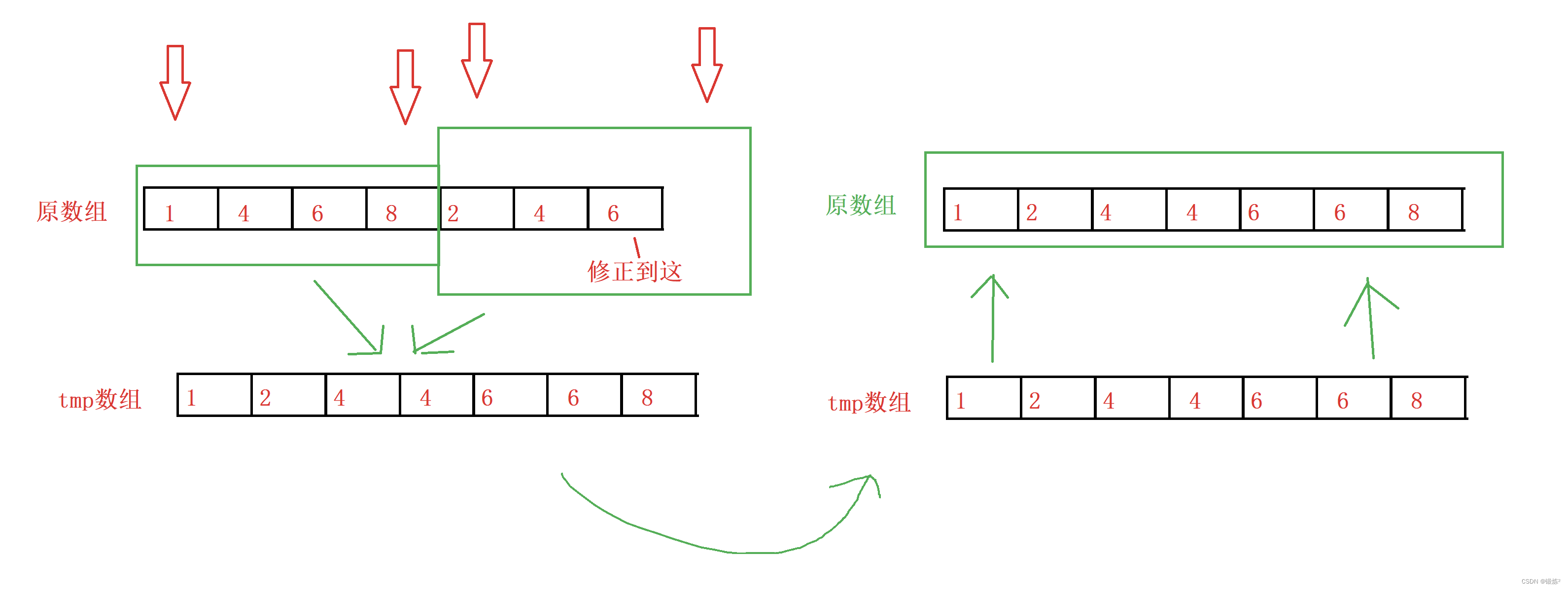
3.1.3 拷贝回原数组

把tmp数组中的内容拷贝回原数组中

3.2 归并过程(非递归)

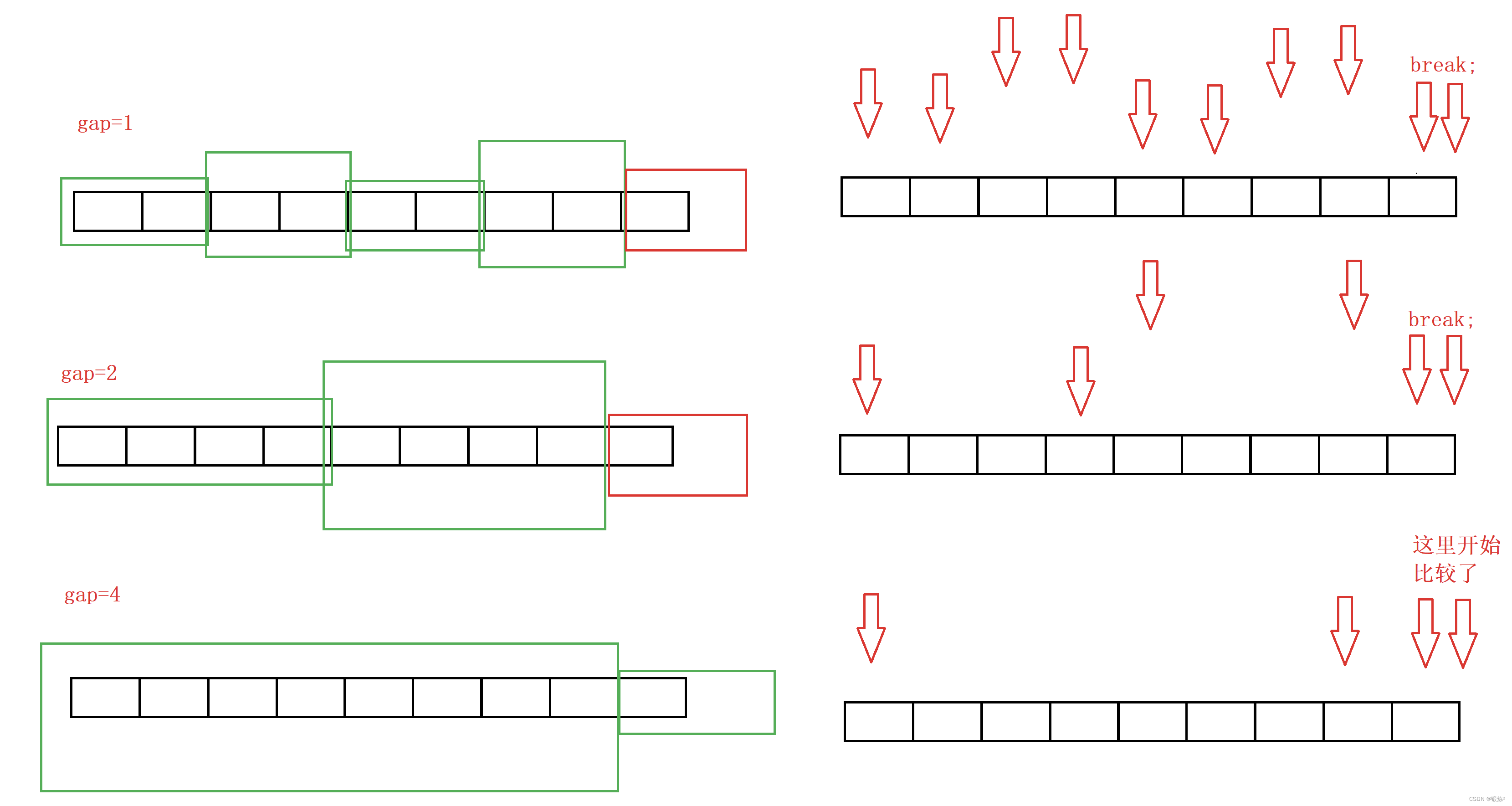
3.2.1 多趟gap

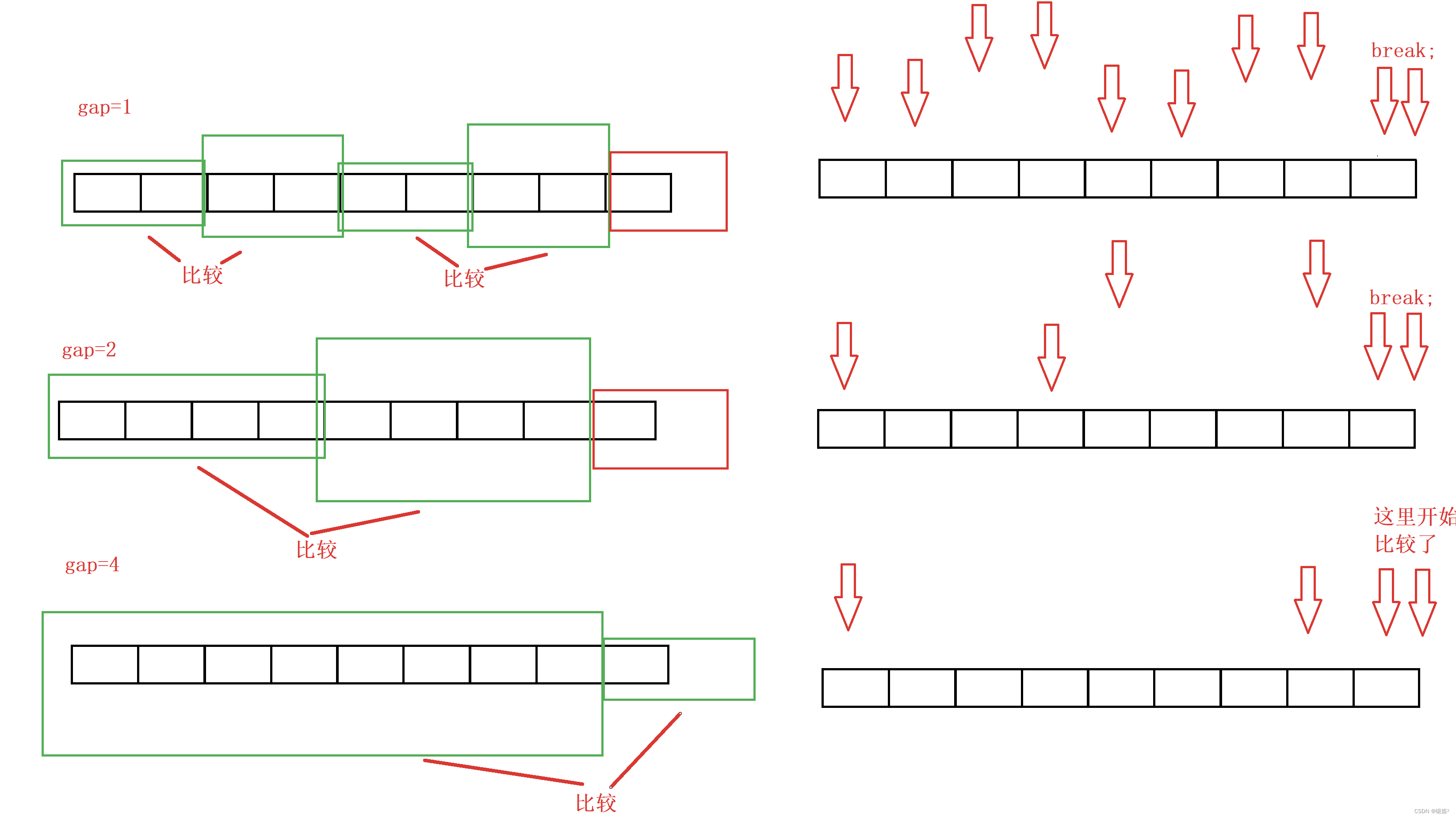
使用多趟gap，对数组需要排序的内容进行调整，这里的gap=gap*2；使用gap的2倍增长模拟归并排序，这里就没有使用递归的方法了。仅仅是数组内存的操作。

void MergeSortNonR(int* a, int n, int* tmp)
{
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;


			//[i, i + gap -1][i + gap, i + 2*gap - 1]
			//修正区间 1.只有一组：
			if (begin2 >= n)
			{
				break;
			}
			//修正区间 2.有两组：右边组没满
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			MergeArr(a, begin1, end1, begin2, end2, tmp);
		}
		gap *= 2;
	}
}

3.2.2 合并过程

通过左右区间进行比较，随着前面的gap的倍数增大，合并过程中的左右区间比较的范围也程倍数增长。2:2合成4    4:4合成8    8:8合成16.........若区间越界则需要处理。

MergeArr(int* a, int begin1, int end1, int begin2, int end2, int*tmp)
{
	int index = begin1;
	int begin = begin1, end = end2;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}

	//拷贝回原数组
	for (int i = begin; i <= end; i++)
	{
		a[i] = tmp[i];
	}

}

 3.3.3 归并(非递归)全部代码

归并排序(非递归全部代码)

void PrintfArry(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}



MergeArr(int* a, int begin1, int end1, int begin2, int end2, int*tmp)
{
	int index = begin1;
	int begin = begin1, end = end2;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}

	//拷贝回原数组
	for (int i = begin; i <= end; i++)
	{
		a[i] = tmp[i];
	}

}

void MergeSortNonR(int* a, int n, int* tmp)
{
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;


			//[i, i + gap -1][i + gap, i + 2*gap - 1]
			//修正区间 1.只有一组：
			if (begin2 >= n)
			{
				break;
			}
			//修正区间 2.有两组：右边组没满
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			MergeArr(a, begin1, end1, begin2, end2, tmp);
		}
		gap *= 2;
	}
}


void TestMergeSortNonR()
{
	int a[] = { 24,67,2,478,2,58,0,43,2,2,561,1,1,3,5,76 };
	int* tmp = malloc(sizeof(int) * sizeof(a) / sizeof(a[0]));
	PrintfArry(a, sizeof(a) / sizeof(a[0]));
	if (tmp == NULL)
		printf("malloc error");

	MergeSortNonR(a,sizeof(a)/sizeof(a[0]),tmp);
	PrintfArry(a, sizeof(a) / sizeof(a[0]));

	free(tmp);
}

int main()
{
	TestMergeSortNonR();
	return 0;	
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1627034.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

开箱机选型攻略：如何挑选适合你的自动化设备?

开箱机选型攻略：如何挑选适合你的自动化设备?

在如今快节奏的生产环境中&#xff0c;自动化设备的运用已成为企业提升效率、降低成本的关键。开箱机作为自动化生产线上的重要一环&#xff0c;其选型对于企业来说至关重要。星派将为您提供一份开箱机选型攻略&#xff0c;帮助您挑选出最适合自己的自动化设备。 一、了解开箱…
阅读更多...
从 Apache Doris 到 SelectDB Cloud：云原生架构下的弹性能力揭秘

从 Apache Doris 到 SelectDB Cloud：云原生架构下的弹性能力揭秘

随着云时代的到来&#xff0c;越来越多企业开始在公有云、私有云乃至 K8s 容器平台构建实时数据平台。云计算基础设施的革新&#xff0c;促使着数据仓库朝着云原生的方向发展。而用户日益复杂的业务负载和降本增效的需求&#xff0c;对于系统资源的精细化管理和成本效益等方面提…
阅读更多...
一种利用合法工具渗透的新型方法

一种利用合法工具渗透的新型方法

摘要 黑客在执行各种攻击步骤时倾向于优先选择合法工具&#xff0c;因为这些工具能帮助他们规避检测系统&#xff0c;同时将恶意软件开发成本降至最低。网络扫描、捕获进程内存转储、数据外泄、远程运行文件&#xff0c;甚至加密驱动器——所有这些都可以通过可信软件完成。为了…
阅读更多...
ubuntu查看opencveigen

ubuntu查看opencveigen

ubuntu查看opencv&eigen&cmake版本的方法 eigen eigen版本号在/usr/include/eigen3/Eigen/src/Core/util/Macros.h文件中&#xff0c;下图代表版本3.3.7 opencv版本 pkg-config --modversion opencv4也可能最后的字符串是opencv2&#xff0c;opencv
阅读更多...
R基本的数据管理

R基本的数据管理

一&#xff0c;创建变量 创建一个数据框 > myData<-data.frame(x1c(1,2,3,4,5,6),x2c(6,5,67,8,9,0)) > myDatax1 x2 1 1 6 2 2 5 3 3 67 4 4 8 5 5 9 6 6 0增加一列为两者的和 > myData$sum<-myData$x1myData$x2 > myDatax1 x2 sum 1 1 6 …
阅读更多...
3d合并的模型为什么没有模型---模大狮模型网

3d合并的模型为什么没有模型---模大狮模型网

在3D建模中&#xff0c;合并模型是常见的操作&#xff0c;它可以将多个模型合并成一个整体。然而&#xff0c;有时候在合并后却发现部分模型消失了&#xff0c;这可能会让人感到困惑和失望。本文将探讨为什么合并的3D模型中会出现没有模型的情况&#xff0c;并提供一些解决方法…
阅读更多...
【Unity动画系统】动画基本原理与Avater骨骼复用

【Unity动画系统】动画基本原理与Avater骨骼复用

动画基本原理 动画片段文件是一个描述物体变化状态的文本文件 在Unity中创建的资源文件大多都是YAML语言编写的文本文件 Curves表示一种变化状态&#xff0c;为空的话则没有记录任何内容 位置变化后的旋转变化状态&#xff1a; 动画文件里的Path名字要相同才能播放相同的动画 …
阅读更多...
数据结构与算法解题-20240426

数据结构与算法解题-20240426

这里写目录标题 面试题 08.04. 幂集367. 有效的完全平方数192. 统计词频747. 至少是其他数字两倍的最大数718. 最长重复子数组 面试题 08.04. 幂集 中等 幂集。编写一种方法&#xff0c;返回某集合的所有子集。集合中不包含重复的元素。 说明&#xff1a;解集不能包含重复的子…
阅读更多...
稳态视觉诱发电位 (SSVEP) 分类学习系列 (3) :3DCNN

稳态视觉诱发电位 (SSVEP) 分类学习系列 (3) :3DCNN

稳态视觉诱发电位分类学习系列:3DCNN 0. 引言1. 主要贡献2. 提出的方法2.1 解码主要步骤2.2 网络具体结构2.3 迁移策略 3. 结果和讨论3.1 数据集1上的结果3.2 数据集2上的结果3.3 零填充 4. 总结欢迎来稿 论文地址&#xff1a;https://www.sciencedirect.com/science/article/a…
阅读更多...
[最新]CentOS7设置开机自启动Hadoop集群

[最新]CentOS7设置开机自启动Hadoop集群

安装好Hadoop后我们可以使用开机自启动的方式&#xff0c;节约敲命令的时间。注意是centOS7版本!!!和centOS6版本区别非常大!!! 1、切换到系统目录 [rootmaster ~]# cd /etc/systemd [rootmaster systemd]# ll total 32 -rw-r--r-- 1 root root 720 Jun 30 23:11 bootcha…
阅读更多...
微信小程序：6.事件

微信小程序：6.事件

什么事事件 事件就是渲染层到逻辑层的通讯方式&#xff0c;比如提交表单&#xff0c;按钮点击都可以看作一个事件。 小程序中常用的事件 事件对象属性列表 当事件回调时&#xff0c;会收到一个事件对象event&#xff0c;他详细属性如夏表所示&#xff1a; target和curren…
阅读更多...
网络安全实训Day16

网络安全实训Day16

网络空间安全实训-渗透测试 漏洞扫描 定义 扫描和探测目标范围内的主机存在哪些安全漏洞&#xff0c;或扫描目标范围内的那些主机存在某个指定的漏洞 漏扫工具 AWVS APPScan MSF 使用MSF扫描漏洞并利用 1.搜索需要的攻击模块 search ms17-010 2.使用攻击模块 use 模块名称…
阅读更多...
改ip地址软件手机怎么弄？分享操作指南与注意事项

改ip地址软件手机怎么弄？分享操作指南与注意事项

随着移动互联网的普及&#xff0c;手机已成为我们日常生活中不可或缺的工具。在某些情况下&#xff0c;我们可能需要更改手机的IP地址&#xff0c;以满足特定的网络需求或实现某些功能。然而&#xff0c;对于许多用户来说&#xff0c;如何在手机上更改IP地址可能是一个相对陌生…
阅读更多...
【Android】 网络技术

【Android】 网络技术

前言 本文用于记录Android网络技术的使用&#xff0c; 包括我们如何发起一条HTTP请求、解析XML、JOSN格式的数据以及最好用的网络库Retrofit。 使用HTTP协议访问网络 关于HTTP协议的工作原理&#xff0c;我们只需要知道客户端向服务器发起一条HTTP请求&#xff0c;服务器接收…
阅读更多...
HarmonyOS开发案例：【rating组件】

HarmonyOS开发案例：【rating组件】

介绍 将引导开发者使用rating组件实现星级打分功能。 相关概念 [rating组件]&#xff1a;评分条&#xff0c;可根据用户判断进行打分。 环境搭建 软件要求 [DevEco Studio]版本&#xff1a;DevEco Studio 3.1 Release及以上版本。OpenHarmony SDK版本&#xff1a;API vers…
阅读更多...
预见预判|AIRIOT智慧交通管理解决方案

预见预判|AIRIOT智慧交通管理解决方案

随着机动车保有量的逐步增加&#xff0c;城市交通压力日益增大。同时&#xff0c;新能源车辆的快速发展虽然带来了环保效益&#xff0c;但也因不限号政策而进一步加剧了道路拥堵问题。此外&#xff0c;各类赛事和重大活动的交通管制措施也时常导致交通状况复杂多变。面对这些挑…
阅读更多...
Linux--MyMiniTry--Vim

Linux--MyMiniTry--Vim

首先下载好vim,我们可以按以下的方式进行光标的移动&#xff08;也可以回车进行换行&#xff09; &#xff08;--> 进入教程&#xff09; &#xff08;初始的时候没有文本&#xff0c;你怎么按都没有用&#xff09; &#xff08;我们要先按 i &#xff0c;进行插入文本才…
阅读更多...
maven修改默认编码格式为UTF-8

maven修改默认编码格式为UTF-8

执行mvn -version查看maven版本信息发现&#xff0c;maven使用的编码格式为GBK。 为什么想到要修改编码格式呢&#xff1f;因为idea中我将文件格式统一设置为UTF-8&#xff08;如果不知道如何修改文件编码&#xff0c;可以参考文末&#xff09;&#xff0c;然后使用maven打包时…
阅读更多...
[GXYCTF 2019]BabyUpload

[GXYCTF 2019]BabyUpload

过滤 <? 且后缀不能有 php 上传1.jpg文件&#xff0c;内容为&#xff1a; <script languagephp>eval($_POST[cmd]);</script> 但文件后缀为.jpg&#xff0c;蚁剑不能连接。那怎么办呢&#xff1f; .htaccess文件&#xff1a;解析.jpg文件中的php代码 &#xf…
阅读更多...
LLaMA-Factory参数的解答（命令，单卡，预训练）

LLaMA-Factory参数的解答（命令，单卡，预训练）

前面这个写过&#xff0c;但觉得写的不是很好&#xff0c;这次是参考命令运行脚本&#xff0c;讲解各个参数含义。后续尽可能会更新&#xff0c;可以关注一下专栏&#xff01;&#xff01; *这是个人写的参数解读&#xff0c;我并非该领域的人如果那个大佬看到有参数解读不对或…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023