我们今天接着来看二叉树的操作，如果还没有看过上一篇的可以点击这里：

https://blog.csdn.net/qq_67693066/article/details/138163494

统计叶子结点个数

叶子结点就是左右孩子都没有的结点：
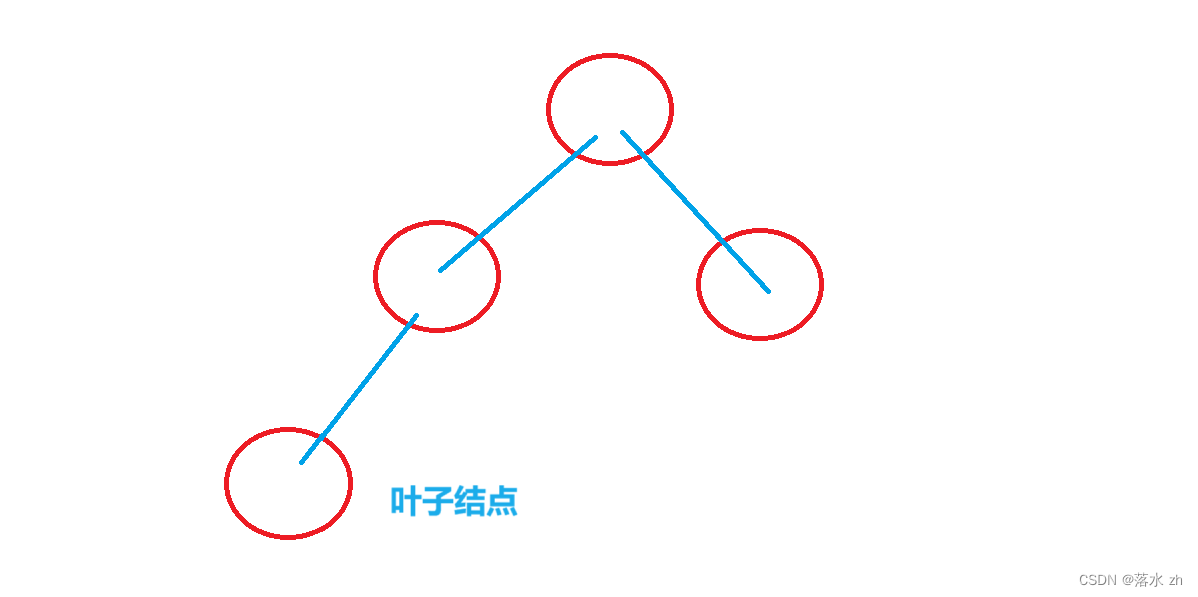判断叶子结点就是判断是否有左右孩子，如果都没有就为叶子结点：

        if(root->_leftChild== nullptr && root->_rightChild == nullptr)
        {
            return 1;
        }

除了判断本身是否为叶子结点，我们也要到它的左右子树去看是否有叶子结点：

       if(root->_leftChild== nullptr && root->_rightChild == nullptr)
        {
            return 1;
        }

        return _TotalLeaves(root->_leftChild) +
        _TotalLeaves(root->_rightChild);

同时，我们要防止空树的情况：

    //叶子结点
    int _TotalLeaves( _Node* const& root)
    {
        if(root == nullptr)
        {
            return 0;
        }

        if(root->_leftChild== nullptr && root->_rightChild == nullptr)
        {
            return 1;
        }

        return _TotalLeaves(root->_leftChild) +
        _TotalLeaves(root->_rightChild);
    }

我们再封装一次：

    //叶子结点个数
    int TotalLeaves()
    {
        return _TotalLeaves(_root);
    }

我们可以测试一下：

#include "BTree.h"

int main()
{
    BTree<int> bt;

    bt.Insert(20);
    bt.Insert(12);
    bt.Insert(35);
    bt.Insert(22);
    bt.Insert(1);

    bt.PrveOrder();
    std::cout<<std::endl;
    bt.InOrder();
    std::cout<<std::endl;
    bt.PostOrder();
    std::cout<<std::endl;

    std::cout <<"叶子结点个数：" << bt.TotalLeaves() << std::endl;

    return 0;
}

统计结点个数

统计结点个数，相对来说更简单，只要是一个结点，我们就返回1，表示一个结点：

    //统计结点个数
    int _NodeNumbers( _Node* const& root)
    {
        //防止空树的情况
        if(root == nullptr)
        {
            return 0;
        }

        return 1;
    }

统计完当前结点，还要统计它的左右子树的结点个数：

    int _NodeNumbers( _Node* const& root)
    {
        //防止空树的情况
        if(root == nullptr)
        {
            return 0;
        }

        return 1 + _NodeNumbers(root->_leftChild)
        + _NodeNumbers(root->_rightChild); //本身 + 它的左右子树
    }

#include "BTree.h"

int main()
{
    BTree<int> bt;

    bt.Insert(20);
    bt.Insert(12);
    bt.Insert(35);
    bt.Insert(22);
    bt.Insert(1);

    bt.PrveOrder();
    std::cout<<std::endl;
    bt.InOrder();
    std::cout<<std::endl;
    bt.PostOrder();
    std::cout<<std::endl;

    std::cout <<"叶子结点个数：" << bt.TotalLeaves() << std::endl;
    std::cout <<"结点个数：" << bt.NodeNumber() << std::endl;

    return 0;
}

层序遍历

层序遍历是一种较为特殊的遍历方式，它不依靠根，左子树，右子树的顺序，它是依靠二叉树的层数来遍历：

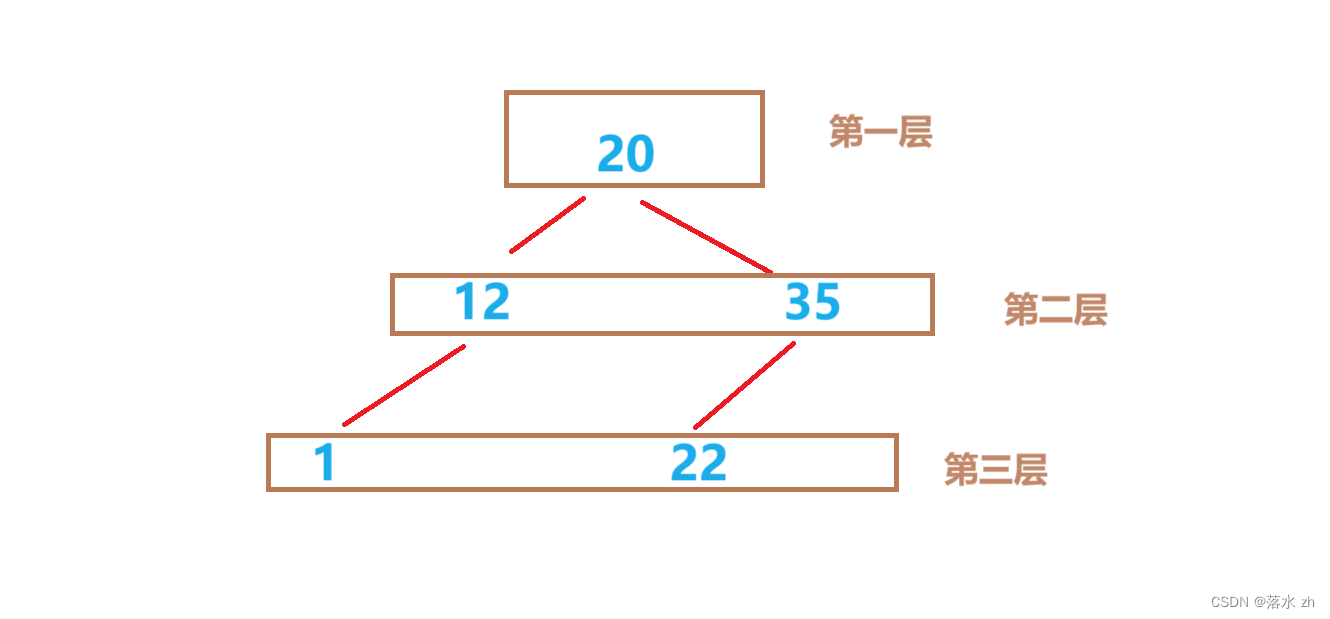
层次遍历是依次遍历各层的元素的算法，这种算法遍历出来就是每层的元素顺序。

层次遍历算法中我们要借助我们之前学过的数据结构——队列，因为在层次遍历算法中，我们依次要打印左孩子，右孩子，所以我们借助队列的性质，先入左孩子，然后出队时，左孩子最先被处理：

首先，每一层我们都可以用一个vector来储存：

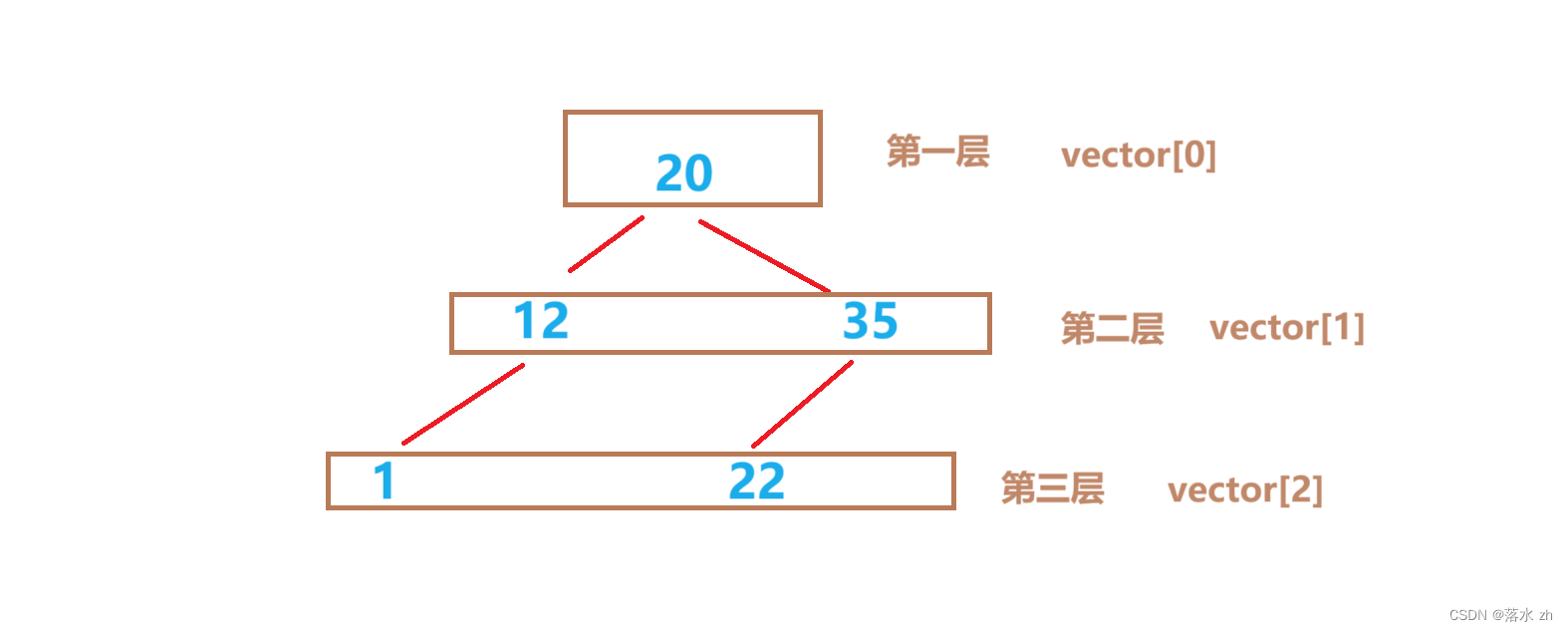
然后用一个大的vector来储存这些vector：

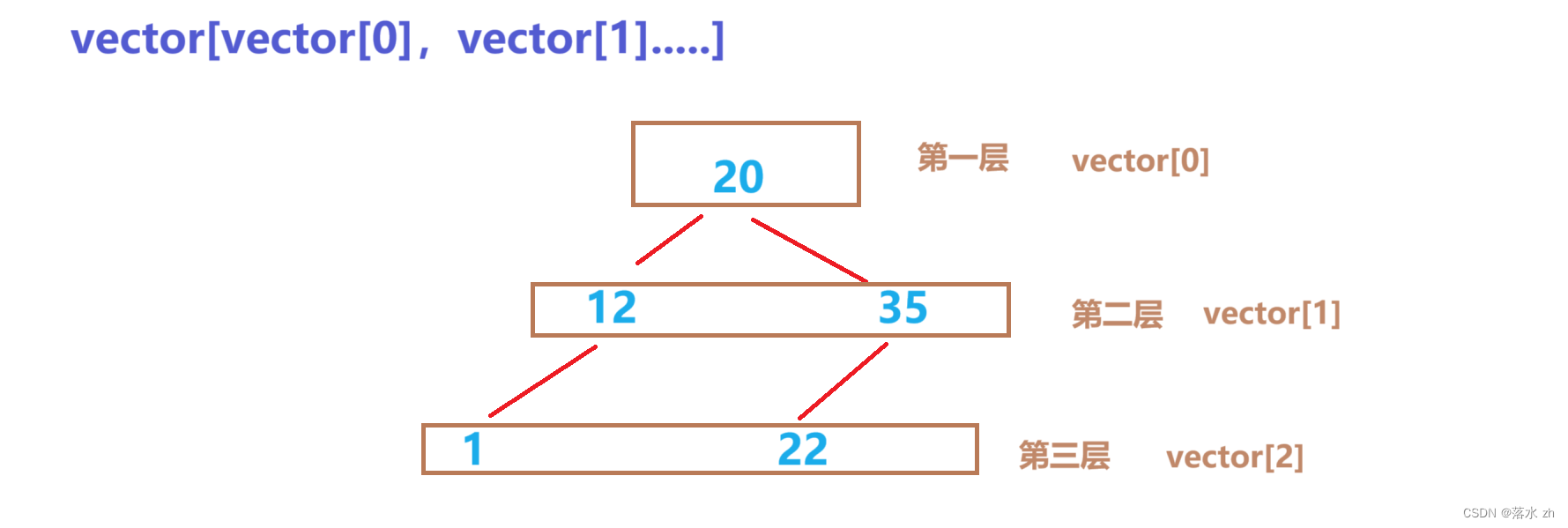
然后我们用queue先压入根节点：
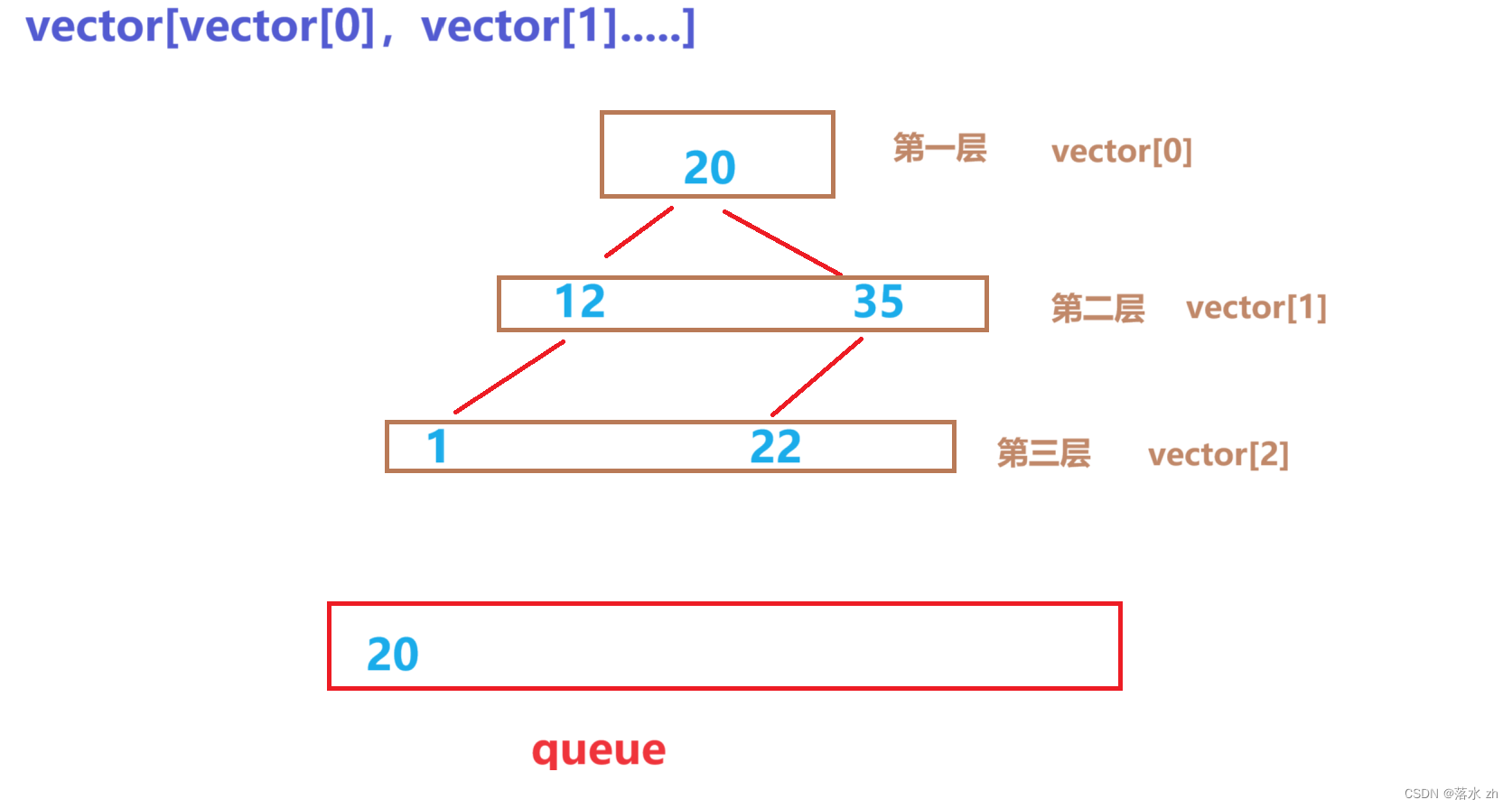然后20是第一层的vector，我们就压入第一层的vector：
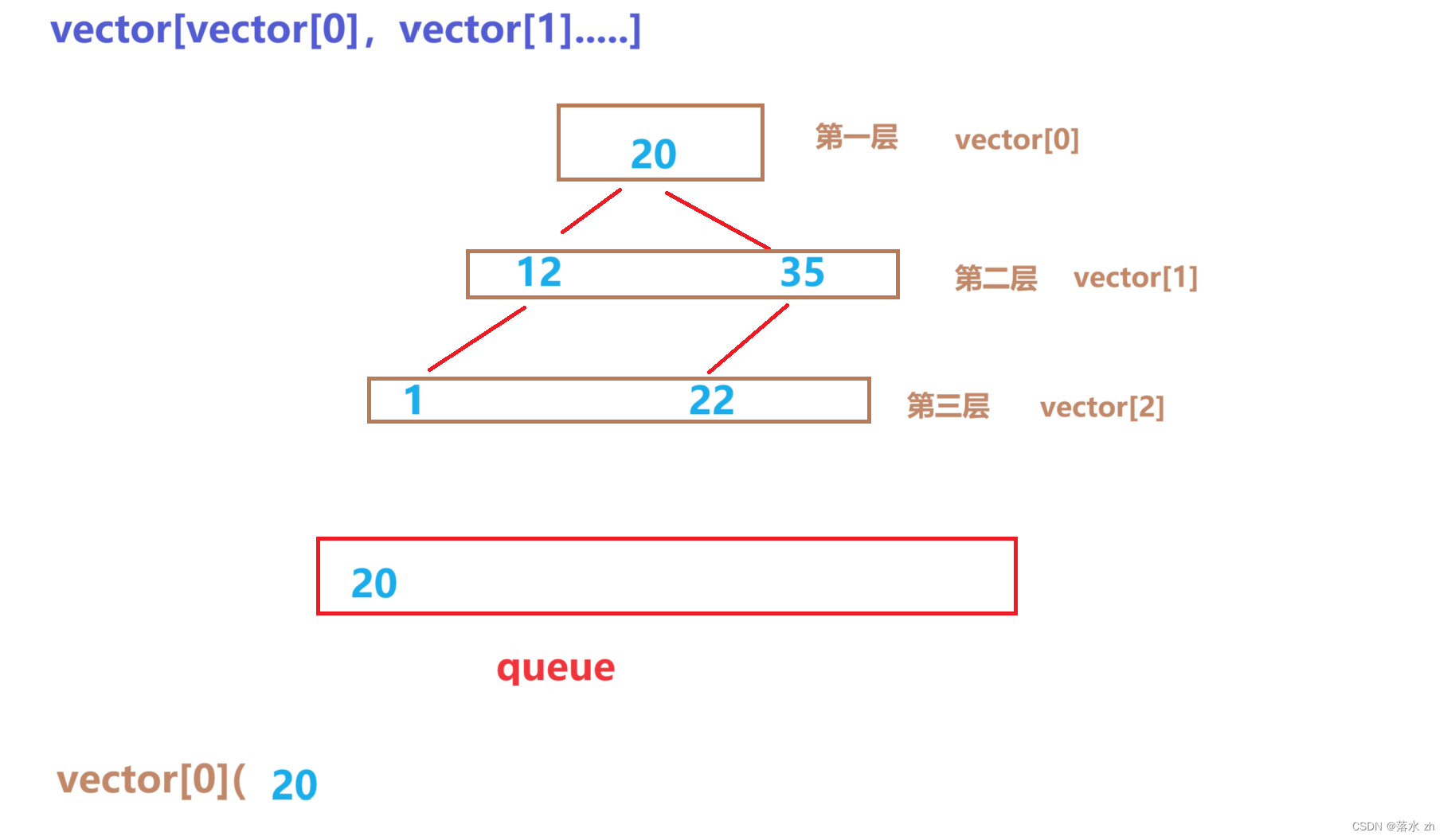然后弹出20，将20的左孩子右孩子压入queue中：

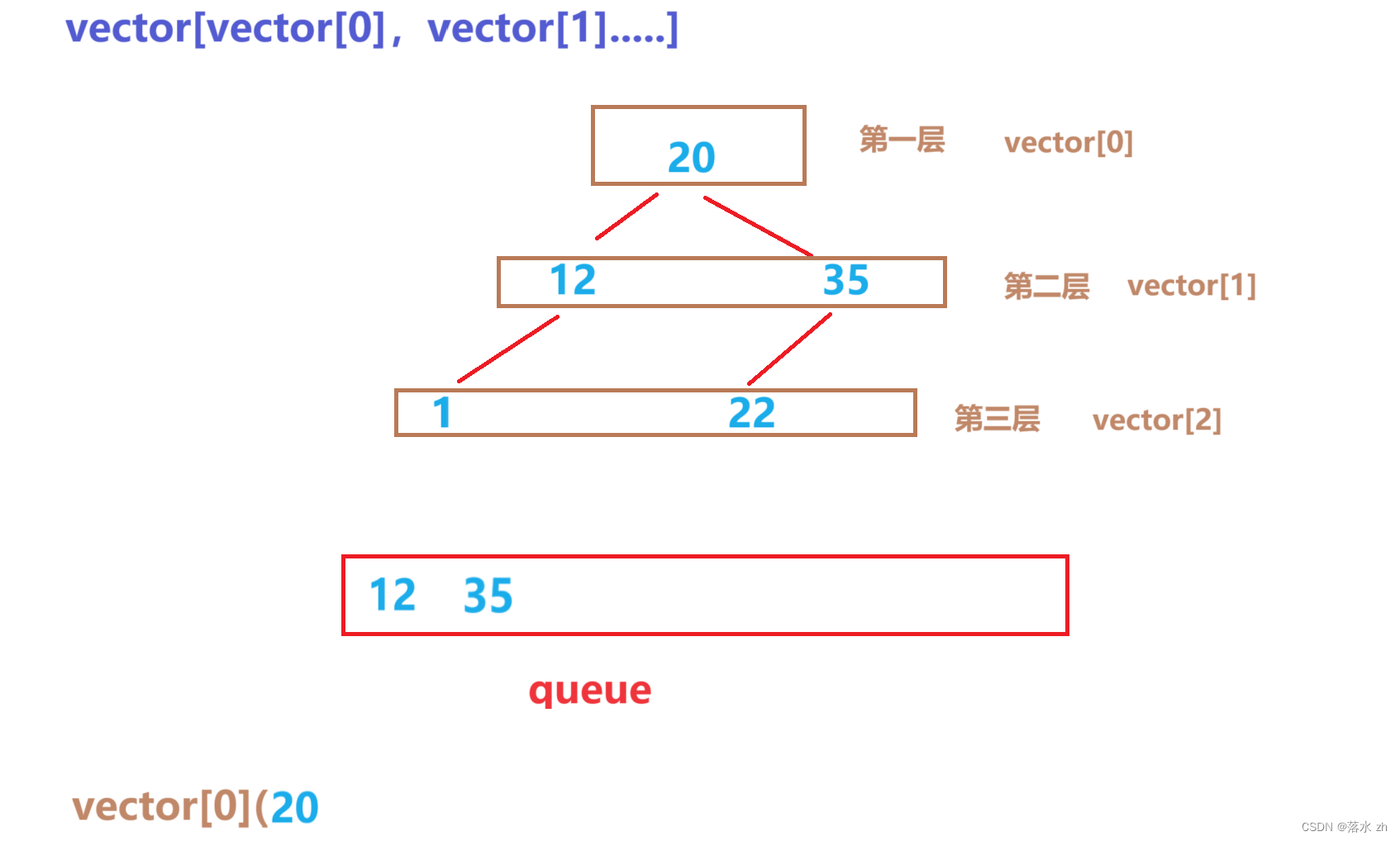
然后将12压入vector[1]，然后将12的左右孩子压入queue：

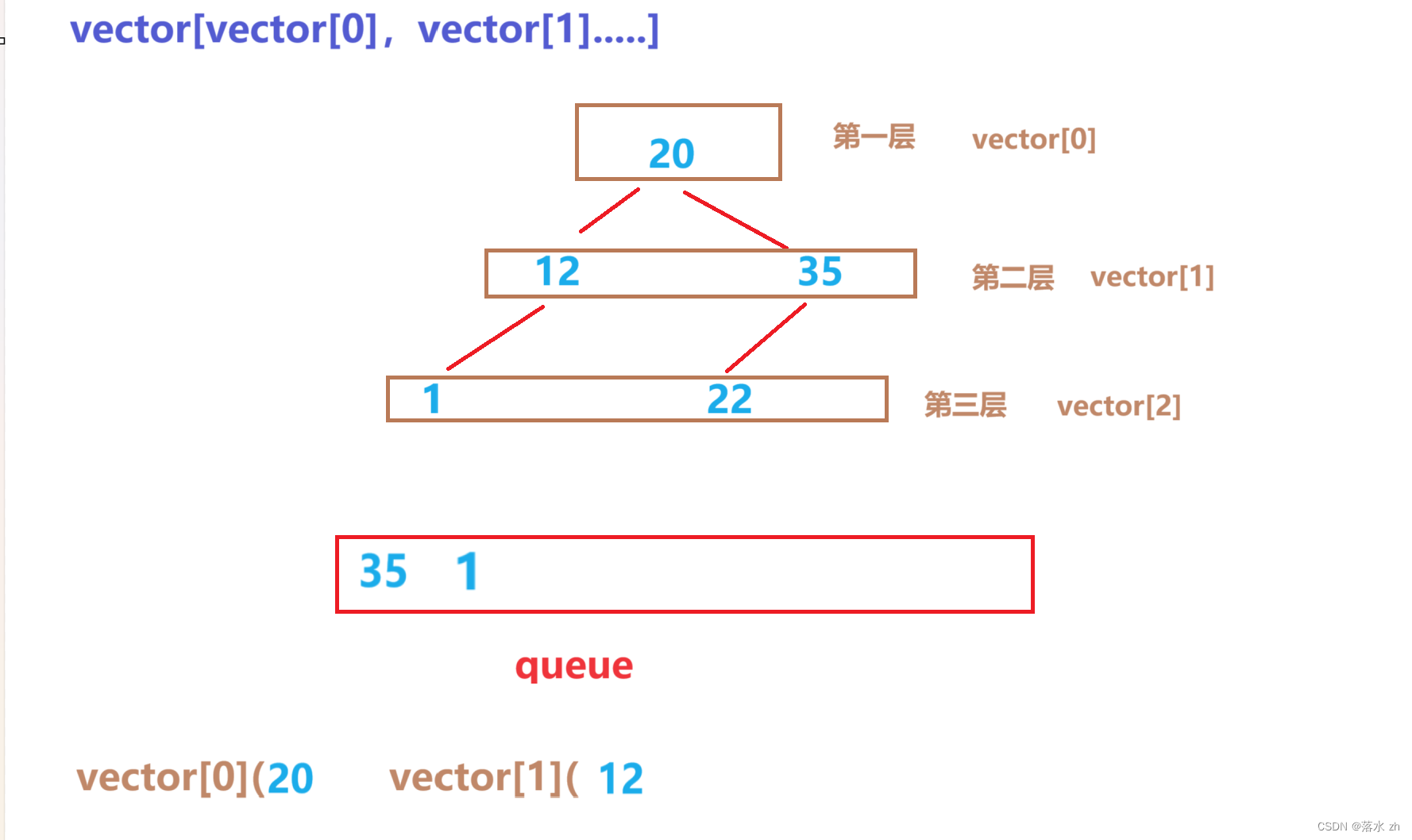然后将35压入vector[1]中，然后同样将35的左右孩子压入queue：
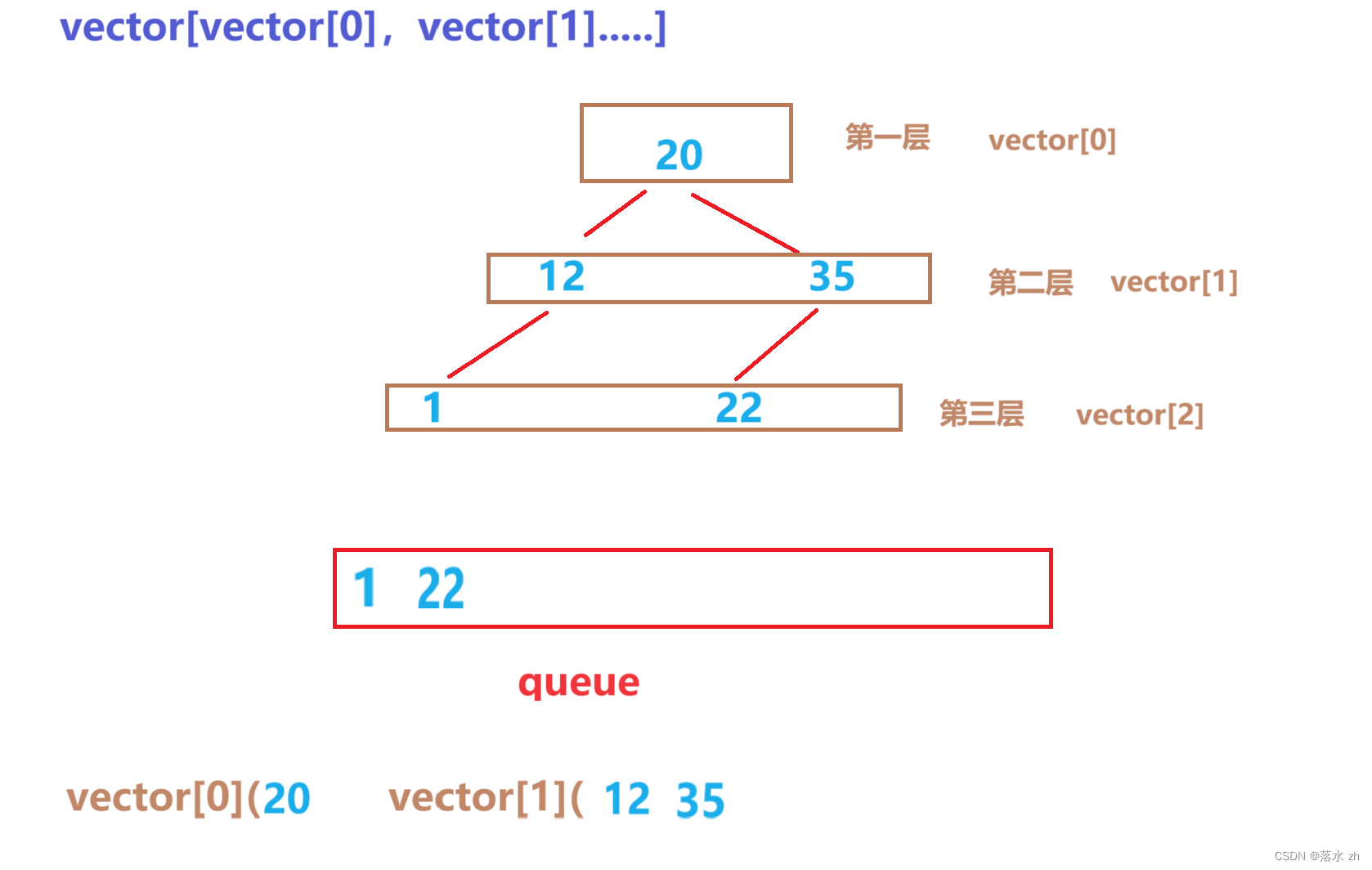然后同样的方法，将剩下的元素压入下一层的vector。了解了思想之后，我们开始写代码：

非递归方式

    // 定义一个函数 LevelOrder，用于实现二叉树的层序遍历
    std::vector<std::vector<T>> _LevelOrder(_Node* const& root)
    {

        // 初始化结果容器，用于存放层序遍历得到的数据，每一层数据作为一个子向量存入
        std::vector<std::vector<T>> result;
        // 使用队列辅助遍历，初始时仅包含根节点
        std::queue<_Node*> queue;

        // 如果根节点为空，则直接返回空结果集
        if (!root)
        {
            return result;
        }

        // 将根节点压入队列
        queue.push(root);
        
        // 当队列非空时，继续进行遍历
        while (!queue.empty())
        {
            // 初始化一个临时向量，用于存储当前层的所有节点数据
            std::vector<T> curResult;

            // 记录当前层队列的大小（即节点数）
            int curSize = queue.size();
            // 遍历当前层的所有节点
            for (int i = 0; i < curSize; i++)
            {
                // 弹出队首节点
                _Node* front = queue.front();
                queue.pop();

                // 将当前节点的数据添加到当前层结果向量中
                curResult.push_back(front->_data);

                // 若当前节点有左子节点，将其压入队列，等待下一层遍历
                if (front->_leftChild)
                    queue.push(front->_leftChild);

                // 若当前节点有右子节点，将其压入队列，等待下一层遍历
                if (front->_rightChild)
                    queue.push(front->_rightChild);
            }

            // 将当前层遍历结果添加到总结果集中
            result.push_back(curResult);
        }

        // 遍历完成后，返回层序遍历结果集
        return result;
    }

递归方式

除了非递归方式，我们发现上面的方式都是一个模子里面刻出来的，所以我们也可以用递归的方式：

如果用递归方式，我们就不用队列来辅助了，因为每一次递归都会开一个新的函数栈帧，我们可以利用这个栈帧来区分层次：

// 定义一个成员函数 LevelOrder，用于获取二叉树的层序遍历结果
std::vector<std::vector<T>> LevelOrder()
{
    // 初始化结果容器，用于存放层序遍历得到的数据，每一层数据作为一个子向量存入
    std::vector<std::vector<T>> result;

    // 调用辅助递归函数，从根节点开始遍历
    LevelOrderHelper(_root, 0, result);

    // 返回层序遍历结果集
    return result;
}

// 定义一个私有辅助递归函数 LevelOrderHelper，用于实现二叉树的层序遍历
void LevelOrderHelper(_Node* root, int level, std::vector<std::vector<T>>& result)
{
    // 如果当前节点为空，直接返回
    if (!root)
    {
        return;
    }

    // 如果当前层级超出了结果容器的范围，添加一个新的子向量
    if (result.size() <= level)
    {
        result.push_back(std::vector<T>());
    }

    // 将当前节点的数据添加到对应层级的子向量中
    result[level].push_back(root->_data);

    // 递归遍历左子树，传入下一层级编号
    LevelOrderHelper(root->_leftChild, level + 1, result);

    // 递归遍历右子树，传入下一层级编号
    LevelOrderHelper(root->_rightChild, level + 1, result);
}

这段代码定义了一个成员函数 LevelOrder，用于获取当前二叉树的层序遍历结果。它首先初始化一个结果容器，然后调用私有辅助递归函数 LevelOrderHelper，从根节点开始遍历，并将遍历结果存储在结果容器中。最后返回这个结果容器。

辅助递归函数 LevelOrderHelper 接收当前节点、所在层级以及结果容器作为参数。递归过程中，首先检查当前节点是否为空，若为空则直接返回。接着检查当前层级是否已存在于结果容器中，若不存在则添加一个新子向量。然后将当前节点数据添加到对应层级的子向量中。最后分别递归遍历左、右子树，传入下一层级编号。