🔗 运行环境:Matlab
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天更新系列——对二维或三维散点数据插值函数scatteredInterpolant💗
📆 最近更新:2024 年 04 月 25 日,左手の明天的第 326 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####
使用 scatteredInterpolant 对散点数据的二维或三维数据集执行插值。scatteredInterpolant 返回给定数据集的差值 F。可以计算一组查询点(例如二维 (xq,yq))处的 F 值,以得出插入的值 vq = F(xq,yq)。
目录
函数描述
输入参数
x, y, z — 样本点
P — 样本点数组
v — 样本点处的函数值
Method — 插值方法
ExtrapolationMethod — 外插方法
示例
二维插值
三维插值
替代样本值
比较散点数据的插值方法
在查询点进行多组值插值
函数描述
F = scatteredInterpolant
F = scatteredInterpolant(x,y,v)x 和 y 指定样本点的 (x,y) 坐标。v 包含与点 (x,y) 关联的样本值。
F = scatteredInterpolant(x,y,z,v)
F = scatteredInterpolant(P,v)P 的行包含 v 中值的 (x, y) 或 (x, y, z) 坐标。
F = scatteredInterpolant(___,Method)'nearest'、'linear' 或 'natural'。在前三个语法中的任意一个中指定 Method 作为最后一个输入参量。
F = scatteredInterpolant(___,Method,ExtrapolationMethod)Method 和 ExtrapolationMethod 作为最后两个输入参量。
-
Method可以是'nearest'、'linear'或'natural'。 -
ExtrapolationMethod可以是'nearest'、'linear'或'none'。
输入参数
x, y, z — 样本点
样本点,指定为列向量,其行数与 v 相同。样本点应该是唯一的。但是,如果样本点包含重复项,scatteredInterpolant 将显示警告并将重复项合并为单个点。
P — 样本点数组
样本点数组,指定为 m×n 的矩阵,其中 m 是点数,n 是这些点所在空间的维度。P 的各行包含样本点的 (x, y) 或 (x, y, z) 坐标。样本点应该是唯一的。
v — 样本点处的函数值
样本点处的函数值,指定为向量或矩阵。对于二维数据,v = F(x,y)。对于三维数据,v = F(x,y,z)。
-
要使用一组值进行插值,请将
v指定为向量,其中行数与样本点数相同。 -
要使用多组值进行插值,请将
v指定为矩阵,其中行数与样本点数相同。v中的每列表示不同函数在样本点的值。例如,如果x和y是包含 10 个元素的列向量,则可以将v指定为 10×4 矩阵以使用四组不同值进行插值。
Method — 插值方法
插值方法,指定为下列选项之一。
| 方法 | 描述 | 连续性 |
|---|---|---|
'linear'(默认值) | 线性插值 | C0 |
'nearest' | 最近邻点插值 | 不连续 |
'natural' | 自然邻点插值 | C1(样本点处除外) |
ExtrapolationMethod — 外插方法
外插法,指定为下列选项之一。
| ExtrapolationMethod | 描述 |
|---|---|
'linear' | 基于边界梯度的线性外插。 |
'nearest' | 最近邻点外插。此方法的计算结果为最近邻点的值。 |
'none' | 无外插。 |
示例
二维插值
定义一些样本点,并计算这些位置的三角函数的值。这些点是用于插值的样本值。
t = linspace(3/4*pi,2*pi,50)';
x = [3*cos(t); 2*cos(t); 0.7*cos(t)];
y = [3*sin(t); 2*sin(t); 0.7*sin(t)];
v = repelem([-0.5; 1.5; 2],length(t));创建插值。
F = scatteredInterpolant(x,y,v);计算位于查询位置 (xq, yq) 处的插值。
tq = linspace(3/4*pi+0.2,2*pi-0.2,40)';
xq = [2.8*cos(tq); 1.7*cos(tq); cos(tq)];
yq = [2.8*sin(tq); 1.7*sin(tq); sin(tq)];
vq = F(xq,yq);绘制结果。
plot3(x,y,v,'.',xq,yq,vq,'.'), grid on
title('Linear Interpolation')
xlabel('x'), ylabel('y'), zlabel('Values')
legend('Sample data','Interpolated query data','Location','Best')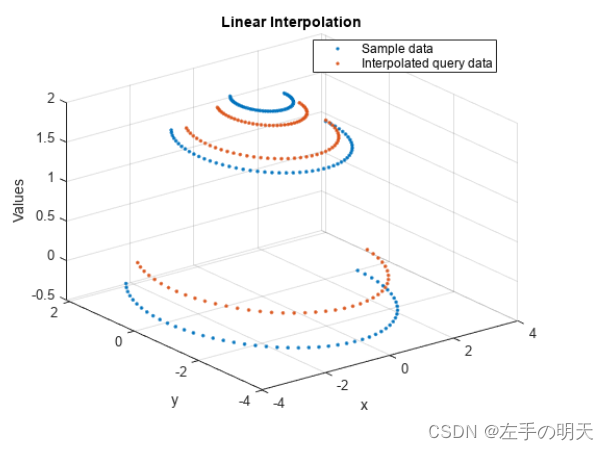
三维插值
为一组散点样本点创建插值,然后计算一组三维查询点处的插值。
定义 200 个随机点并对三角函数采样。这些点是用于插值的样本值。
rng default;
P = -2.5 + 5*rand([200 3]);
v = sin(P(:,1).^2 + P(:,2).^2 + P(:,3).^2)./(P(:,1).^2+P(:,2).^2+P(:,3).^2);创建插值。
F = scatteredInterpolant(P,v);计算位于查询位置 (xq,yq,zq) 处的插值。
[xq,yq,zq] = meshgrid(-2:0.25:2);
vq = F(xq,yq,zq);绘制结果的切片。
xslice = [-.5,1,2];
yslice = [0,2];
zslice = [-2,0];
slice(xq,yq,zq,vq,xslice,yslice,zslice) 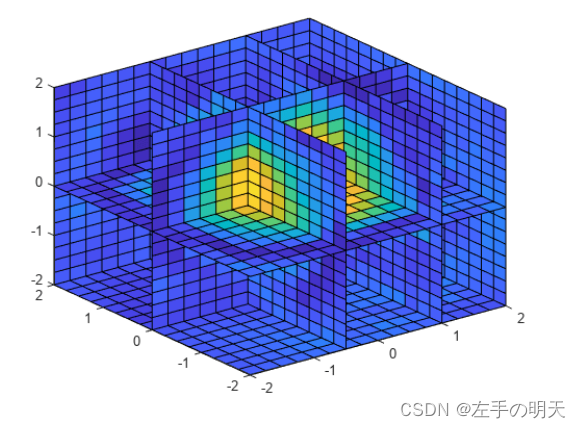
替代样本值
在需要更改位于样本点处的值时替换 Values 属性中的元素。由于原始三角剖分没有改变,因此在计算新插值时可立即获得结果。
创建 50 个随机点并对指数函数进行采样。这些点是用于插值的样本值。
rng('default')
x = -2.5 + 5*rand([50 1]);
y = -2.5 + 5*rand([50 1]);
v = x.*exp(-x.^2-y.^2);创建插值。
F = scatteredInterpolant(x,y,v)F =
scatteredInterpolant with properties:
Points: [50x2 double]
Values: [50x1 double]
Method: 'linear'
ExtrapolationMethod: 'linear'
在 (1.40,1.90) 处计算插值。
F(1.40,1.90)ans = 0.0069
更改插值样本值,并重新计算同一点处的插值。
vnew = x.^2 + y.^2;
F.Values = vnew;
F(1.40,1.90)ans = 5.6491
比较散点数据的插值方法
比较 scatteredInterpolant 提供的几种不同插值算法的结果。
创建包含 50 个散点的样本数据集。这里有意使用较少的点数量,目的是为了突出插值方法之间的差异。
x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);
v = sin(x).^4 .* cos(y);创建插值和查询点网格。
F = scatteredInterpolant(x,y,v);
[xq,yq] = meshgrid(-3:0.1:3);使用 'nearest'、'linear' 和 'natural' 方法绘制结果图。每当插值方法更改时,都需要重新查询插值以获取更新后的结果。
F.Method = 'nearest';
vq1 = F(xq,yq);
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq1)
title('Nearest Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')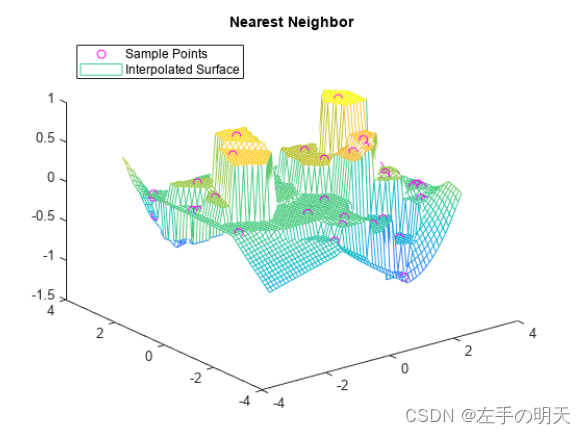
F.Method = 'linear';
vq2 = F(xq,yq);
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq2)
title('Linear')
legend('Sample Points','Interpolated Surface','Location','NorthWest')
F.Method = 'natural';
vq3 = F(xq,yq);
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq3)
title('Natural Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')
绘制精确解。
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,sin(xq).^4 .* cos(yq))
title('Exact Solution')
legend('Sample Points','Exact Surface','Location','NorthWest')
在查询点进行多组值插值
在相同的查询点对多个数据集进行插值。
创建一个包含 50 个散点的样本数据集,由样本点向量 x 和 y 表示。
rng("default")
x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);要对多个数据集进行插值,请创建一个矩阵,其中每列表示不同函数在样本点的值。
s1 = sin(x).^4 .* cos(y);
s2 = sin(x) + cos(y);
s3 = x + y;
s4 = x.^2 + y;
v = [s1 s2 s3 s4];创建查询点向量,指示为 v 中的每组值执行插值的位置。
xq = -3:0.1:3;
yq = -3:0.1:3;创建插值 F。
F = scatteredInterpolant(x,y,v)F =
scatteredInterpolant with properties:
Points: [50x2 double]
Values: [50x4 double]
Method: 'linear'
ExtrapolationMethod: 'linear'
计算位于查询位置的插值。Vq 的每页都包含 v 中对应数据集的插值。
Vq = F({xq,yq});
size(Vq)ans = 1×3
61 61 4
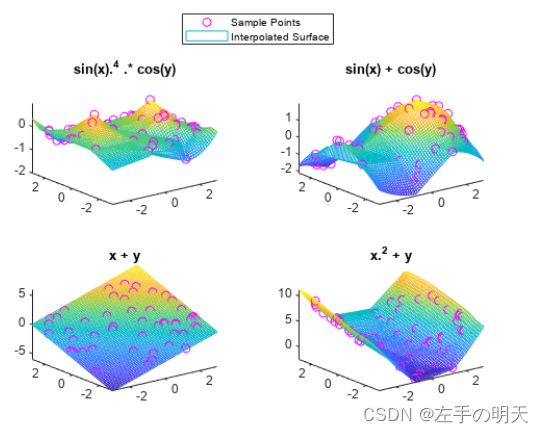
绘制每个数据集的插值。
tiledlayout(2,2)
nexttile
plot3(x,y,v(:,1),'mo')
hold on
mesh(xq,yq,Vq(:,:,1)')
title("sin(x).^4 .* cos(y)")
nexttile
plot3(x,y,v(:,2),'mo')
hold on
mesh(xq,yq,Vq(:,:,2)')
title("sin(x) + cos(y)")
nexttile
plot3(x,y,v(:,3),'mo')
hold on
mesh(xq,yq,Vq(:,:,3)')
title("x + y")
nexttile
plot3(x,y,v(:,4),'mo')
hold on
mesh(xq,yq,Vq(:,:,4)')
title("x.^2 + y")
lg = legend("Sample Points","Interpolated Surface");
lg.Layout.Tile = "north";