0.概述

介绍有序向量二分查找算法的改进思路和原理、实现方式、复杂度分析。

1.语义定义

在有序向量区间V[lo,hi)中，约定search()接口返回不大于e的最后一个元素。

2. 二分查找（版本A）

2.1 原理

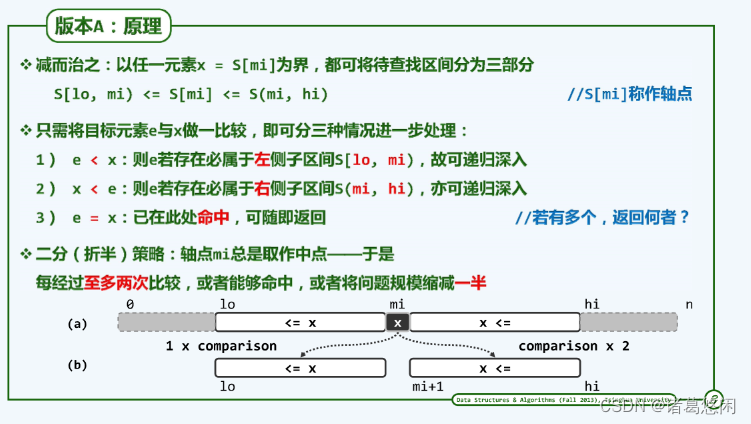
每经过至多两次比较操作，可以将查找问题简化为一个规模更小的新问题。如此，借助递归机制即可便捷地描述和实现此类算法。

2.2 实现

算法思想：减而治之

// 二分查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> 
static Rank binSearch ( T* A, T const& e, Rank lo, Rank hi ) {
	while ( lo < hi ) { //每步迭代可能要做两次比较判断，有三个分支
		Rank mi = ( lo + hi ) >> 1; //以中点为轴点
		if ( e < A[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
		else if ( A[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
		else return mi; //在mi处命中
	} //成功查找可以提前终止
	return -1; //查找失败
} //有多个命中元素时，不能保证返回秩最大者；查找失败时，简单地迒回-1，而且能指示失败的位置

• 通过快捷的整数移位操作回避了相对更加耗时的除法运算。
• 通过引入lo、hi和mi等变量，将减治算法通常的递归模式改成了迭代模式。（递归消除）

2.3 复杂度

随着迭代的不断深入，有效的查找区间宽度将按1/2的比例以几何级数的速度递减。经过至多log2(hi - lo)步迭代后，算法必然终止。故总体时间复杂度不超过：
O($lo{g}_2(hi-lo)$) = O(logn)
上图中的递归公式也可得出这个结论，递推公式不熟悉的可以看递推分析。

顺序查找算法的O(n)复杂度相比无序向量的查找find()无序向量，O(logn)几乎改进了一个线性因子（任意c > 0,logn = O($n^c$)）。

2.4 查找长度

查找算法的整体效率主要地取决于其中所执行的元素大小比较操作的次数，即所谓查找长度。

通常，需分别针对成功与失败查找，从最好、最坏、平均等角度评估

结论：版本A二分查找成功、失败时的平均查找长度均大致为O（1.5logn）

3.Fibonacci查找

3.1 改进思路

解决问题的思路：

1. 其一，调整前、后区域的宽度，适当地加长（缩短）前（后）子向量 （此方法本次采用）
2. 其二，统一沿两个方向深入所需要执行的比较次数，比如都统一为一次（此方法后面改进版本采用）

3.2 黄金分割

实际上，减治策略本身并不要求子向量切分点mi必须居中，故按上述改进思路，不妨按黄金分割比来确定mi。

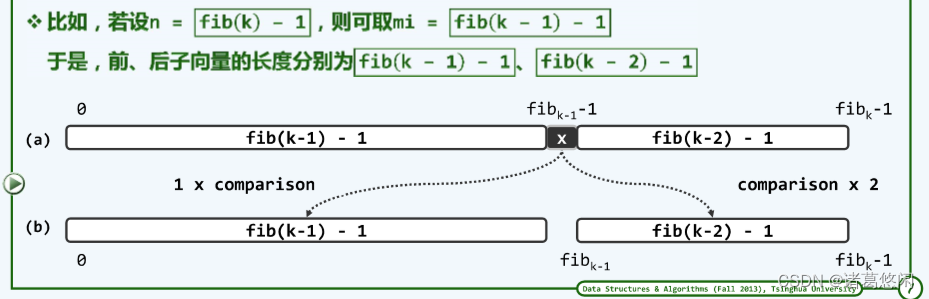
3.3 实现

算法思路：减治策略——黄金分割比来确定mi

#include "..\fibonacci\Fib.h" //引入Fib数列类
// Fibonacci查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch ( T* A, T const& e, Rank lo, Rank hi ) {
	Fib fib ( hi - lo ); //用O(log_phi(n = hi - lo)时间创建Fib数列
	while ( lo < hi ) { //每步迭代可能要做两次比较判断，有三个分支
		while ( hi - lo < fib.get() ) fib.prev(); //通过向前顺序查找（分摊O(1)）——至多迭代几次？
		Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点
		if ( e < A[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
		else if ( A[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
		else  return mi; //在mi处命中
	} //成功查找可以提前终止
	return -1; //查找失败
} //有多个命中元素时，不能保证返回秩最大者；失败时，简单地迒回-1，而且能指示失败的位置

对Fib数不清楚得可以看算法设计优化——Fibonacci数

3.4 复杂度分析

进入循环之前调用构造器Fib(n = hi - lo)，将初始长度设置为“不小于n的最小Fibonacci项”。这一步所需花费的O($lo{g}_{\varphi }$n)时间，分摊到后续O($lo{g}_{\varphi }$n)步迭代中，并不影响算法整体的渐进复杂度。

3.5 平均查找长度

结论：O(1.44∙log2n)

4. 二分查找（版本B）

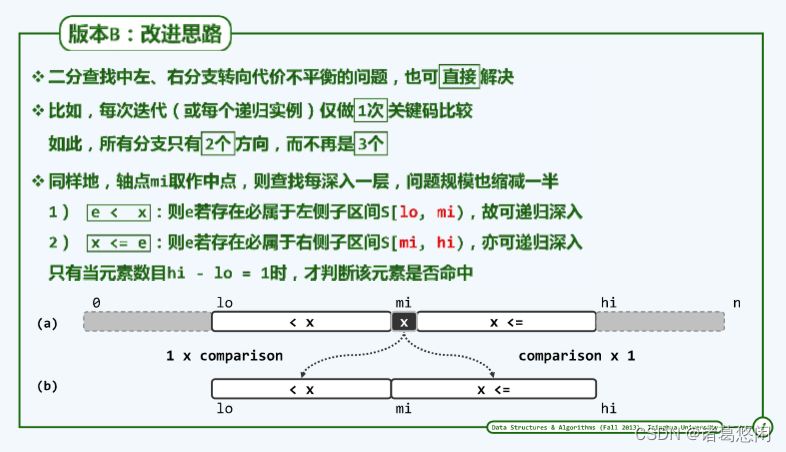
4.1 改进思路

与二分查找算法的版本A基本类似。不同之处是，在每个切分点A[mi]处，仅做一次元素比较。

4.2 实现

// 二分查找算法（版本B）：在有序向量癿匙间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> 
static Rank binSearch ( T* A, T const& e, Rank lo, Rank hi ) {
	while ( 1 < hi - lo ) { //每步迭代仅需做一次比较判断，有两个分支；成功查找不能提前终止
		Rank mi = ( lo + hi ) >> 1; //以中点为轴点
		( e < A[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)
	} //出口时hi = lo + 1，查找匙间仅含一个元素A[lo]
	return ( e == A[lo] ) ? lo : -1 ; //查找成功时返回对应的秩；否则统一返回-1
} //有多个命中元素时，不能保证迒回秩最大者；查找失败时，简单地返回-1，而不能指示失败癿位置

4.3 性能

版本B中的后端子向量需要加入A[mi]，但得益于mi总是位于中央位置，整个算法O(logn)的渐进复杂度不受任何影响。

在这一版本中，只有在向量有效区间宽度缩短至1个单元时算法才会终止，而不能如版本A那样，一旦命中就能及时返回。因此，最好情况下的效率有所倒退。当然，作为补偿，最坏情况下的效率相应地有所提高。实际上无论是成功查找或失败查找，版本B各分支的查找长度更加接近，故整体性能更趋稳定。

4.4 进一步的要求

• 通过查找操作不仅能够确定可行的插入位置，而且能够在同时存在多个可行位置时保证返回其中的秩最大者。

• 在查找失败时返回不大（小）于e的最后（前）一个元素，以便将e作为其后继（前驱）插入向量。

5. 二分查找（版本C）

5.1 实现

// 二分查找算法（版本C）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> 
static Rank binSearch ( T* A, T const& e, Rank lo, Rank hi ) {
	while ( lo < hi ) { //每步迭代仅需做一次比较判断，有两个分支
		Rank mi = ( lo + hi ) >> 1; //以中点为轴点
		( e < A[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)戒(mi, hi)
	} //成功查找不能提前终止
	return --lo; //循环结束时，lo为大于e的元素的最小秩，故lo - 1即不大于e的元素的最大秩
} //有多个命中元素时，总能保证返回秩最大者；查找失败时，能够返回失败的位置

5.2 正确性

版本C与版本B的差异，主要有三点。首先，只有当有效区间的宽度缩短至0（而不是1）时，查找方告终止。另外，在每次转入后端分支时，子向量的左边界取作mi + 1而不是mi。

版本C中的循环体，具有如下不变性：
A[0, lo)中的元素皆不大于e；A[hi, n)中的元素皆大于e

首次迭代时，lo = 0且hi = n，A[0, lo)和A[hi, n)均空，不变性自然成立。
如图所示，设在某次进入循环时以上不变性成立，以下无非两种情况。若e < A[mi]，则如图(b)，在令hi = mi并使A[hi, n)向左扩展之后，该区间内的元素皆不小于A[mi]，当然也仍然大于e。反之，若A[mi] ≤ e，则如图©，在令lo = mi + 1并使A[0, lo)向右拓展之后，该区间内的元素皆不大于A[mi]，当然也仍然不大于e。总之，上述不变性必然得以延续。

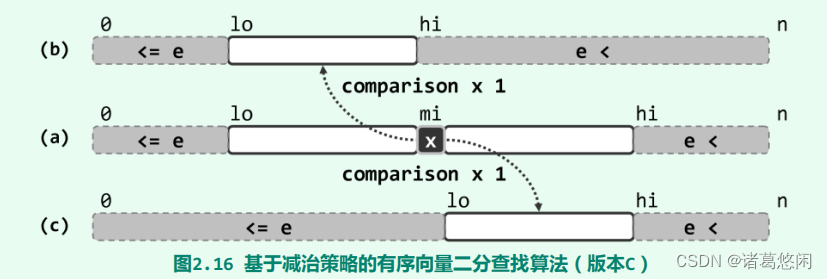
循环终止时，lo = hi。考查此时的元素A[lo - 1]和A[lo]：作为A[0, lo)内的最后一个元素，A[lo - 1]必不大于e；作为A[lo, n) = A[hi, n)内的第一个元素，A[lo]必大于e。也就是说，A[lo - 1]即是原向量中不大于e的最后一个元素。因此在循环结束之后，无论成功与否，只需返回lo - 1即可——这也是版本C与版本B的第三点差异。