目录
一、简介
二、具体步骤
样例:
三、代码
四、结果
五、问题与解决
一、简介
CART(Classification and Regression Trees)是一种常用的决策树算法,可用于分类和回归任务。这个算法由Breiman等人于1984年提出,它的主要思想是通过递归地将数据集划分为两个子集,然后在每个子集上继续划分,直到满足某个停止条件为止。
CART算法在分类和回归问题上表现良好,并且能够处理多种数据类型(包括离散型和连续型特征)。由于其简单、易于理解和实现,以及在一些应用中的良好性能,CART算法被广泛应用于实践中。
二、具体步骤
-
计算整体数据集的基尼指数:
- 首先,计算整个数据集的基尼指数。基尼指数表示从数据集中随机选择两个样本,它们属于不同类别的概率。对于每个节点,基尼指数可以通过以下公式计算:
( D ) 是当前节点的数据集,( k ) 是类别的数量,( p_i ) 是第 ( i ) 类样本在数据集 ( D ) 中的频率。
- 首先,计算整个数据集的基尼指数。基尼指数表示从数据集中随机选择两个样本,它们属于不同类别的概率。对于每个节点,基尼指数可以通过以下公式计算:
-
选择最佳特征和切分点:
- 对于每个特征,遍历其所有可能的取值作为切分点。
- 对于每个切分点,将数据集分为两个子集:左子集(特征值小于等于切分点)和右子集(特征值大于切分点)。
- 计算基尼指数来衡量使用当前特征和切分点进行划分后的加权基尼指数。数学上,对于一个特征 ( A ) 的某个切分点 ( t ),其左子集和右子集的基尼指数可以计算为:
- 选择使得基尼指数最小的特征和切分点作为当前节点的划分依据。
-
递归划分子集:
- 根据选择的最佳特征和切分点,将当前节点的数据集划分为两个子集:左子集和右子集。
- 对每个子集递归地重复步骤 1 和步骤 2,直到达到停止条件,例如达到最大深度、节点样本数量小于预设阈值等。
-
停止条件:
- 决策树构建过程中,需要设定停止条件,以防止过度拟合或无限生长。常见的停止条件包括:达到最大深度、节点样本数量小于预设阈值、节点基尼指数低于阈值等。
-
剪枝:
- 在决策树生长完成后,可以应用剪枝来降低树的复杂度和提高泛化能力。剪枝的目标是通过移除部分节点或子树来减小模型的复杂度,常见的剪枝方法有预剪枝和后剪枝。
- 预剪枝:预剪枝是在决策树构建过程中,在决策树生长过程中进行判断并提前终止树的生长。在预剪枝中,可以设置一些停止生长的条件,例如限制树的最大深度、节点中最小样本数、基尼不纯度的阈值等。当达到任何一个预设条件时,就停止分裂节点并将该节点标记为叶子节点,不再继续向下生长,从而避免过拟合。
-
后剪枝:后剪枝是在决策树构建完成之后,对已生成的决策树进行修剪来减少过拟合。后剪枝通过剪掉一些子树或者将子树替换为叶子节点来减少树的复杂度,从而提高泛化能力。后剪枝的过程通常是自底向上地遍历决策树,然后对每个内部节点尝试剪枝,判断剪枝后的决策树性能是否提升,如果提升则进行剪枝操作。
-
预剪枝和后剪枝各有优劣势:预剪枝可以在构建树的过程中避免过拟合,但可能会导致欠拟合,因为它在生长时就限制了树的复杂度。后剪枝在构建完整个树后进行修剪,更容易实现,但可能会由于过拟合而导致剪枝效果不佳。
-
预测:
- 使用生成的决策树对新样本进行分类预测。
- 从根节点开始,根据特征值逐步向下遍历树的分支,直到到达叶子节点,然后将叶子节点的预测值作为样本的预测结果。
样例:
一些解释:
分裂阈值是决策树算法中用来划分数据集的一个值,它决定了将数据集分成两部分的标准。在每个节点上,决策树算法会选择一个特征和一个分裂阈值,将数据集分为两部分,使得分裂后的子集尽可能地纯净(即属于同一类别)。
假设有一个二维数据集,包含两个特征和一个类别:
| X1 | X2 | Y |
|---|---|---|
| 1.0 | 2.0 | 0 |
| 2.0 | 3.0 | 0 |
| 2.0 | 2.0 | 1 |
| 3.0 | 4.0 | 1 |
| 3.0 | 3.0 | 0 |
在构建过程中,需要选择一个特征和一个分裂阈值来将数据集划分为左右两个子集。假设现在可以选择特征X1,并将分裂阈值设为2.5。所有X1小于2.5的样本将被划分到左子集,而X1大于等于2.5的样本将被划分到右子集。
首先,我们根据选定的特征和分裂阈值将数据集划分成两个子集。
左子集(X1 < 2.5):
| X1 | X2 | Y |
|---|---|---|
| 1.0 | 2.0 | 0 |
| 2.0 | 3.0 | 0 |
| 2.0 | 2.0 | 1 |
右子集(X1 >= 2.5):
| X1 | X2 | Y |
|---|---|---|
| 3.0 | 4.0 | 1 |
| 3.0 | 3.0 | 0 |
对于左子集:
- 类别0的频率:
- 类别1的频率:
左子集的基尼指数为:
对于右子集:
- 类别0的频率:
- 类别1的频率:
右子集的基尼指数为:
计算加权基尼指数
在这个例子中,选定特征X1和分裂阈值2.5的加权基尼指数为约0.66532。
三、代码
import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
class DecisionTreeClassifier:
def __init__(self, max_depth=None, min_samples_split=2):
"""
初始化决策树分类器
参数:
- max_depth: 决策树的最大深度,控制树的生长。默认为None,表示不限制深度。
- min_samples_split: 内部节点再划分所需的最小样本数。默认为2。
"""
self.max_depth = max_depth
self.min_samples_split = min_samples_split
def fit(self, X, y):
"""
根据训练数据拟合模型
参数:
- X: 训练数据的特征数组。
- y: 训练数据的标签数组。
"""
self.n_classes = len(np.unique(y))
self.n_features = X.shape[1]
self.tree_ = self._grow_tree(X, y)
def _grow_tree(self, X, y, depth=0):
"""
递归地构建决策树
参数:
- X: 当前节点的特征数组。
- y: 当前节点的标签数组。
- depth: 当前节点的深度。
"""
# 计算每个类别的样本数
n_samples_per_class = [np.sum(y == i) for i in range(self.n_classes)]
# 预测当前节点的类别为样本数最多的类别
predicted_class = np.argmax(n_samples_per_class)
if depth < self.max_depth and X.shape[0] >= self.min_samples_split:
best_gini = float('inf')
best_feature = None
best_threshold = None
# 遍历每个特征
for feature in range(self.n_features):
unique_values = np.unique(X[:, feature])
# 遍历每个特征值作为分裂阈值
for threshold in unique_values:
y_left = y[X[:, feature] < threshold]
y_right = y[X[:, feature] >= threshold]
if len(y_left) == 0 or len(y_right) == 0:
continue
# 计算基尼不纯度
gini = self._gini_impurity(y_left, y_right)
# 选择最小基尼不纯度对应的特征和阈值
if gini < best_gini:
best_gini = gini
best_feature = feature
best_threshold = threshold
# 如果存在可以降低基尼不纯度的分裂,则继续构建子树
if best_gini < float('inf'):
left_indices = X[:, best_feature] < best_threshold
X_left, y_left = X[left_indices], y[left_indices]
X_right, y_right = X[~left_indices], y[~left_indices]
left_subtree = self._grow_tree(X_left, y_left, depth + 1)
right_subtree = self._grow_tree(X_right, y_right, depth + 1)
return {'feature': best_feature, 'threshold': best_threshold,
'left': left_subtree, 'right': right_subtree}
# 当无法继续分裂时,返回当前节点的预测类别
return {'predicted_class': predicted_class}
def _gini_impurity(self, y_left, y_right):
"""
计算基尼不纯度
参数:
- y_left: 左子节点的标签数组。
- y_right: 右子节点的标签数组。
"""
n_left, n_right = len(y_left), len(y_right)
n_total = n_left + n_right
p_left = np.array([np.sum(y_left == c) / n_left for c in range(self.n_classes)])
p_right = np.array([np.sum(y_right == c) / n_right for c in range(self.n_classes)])
# 计算左右节点的基尼不纯度
gini_left = 1.0 - np.sum(p_left ** 2)
gini_right = 1.0 - np.sum(p_right ** 2)
# 计算加权基尼不纯度
gini = (n_left / n_total) * gini_left + (n_right / n_total) * gini_right
return gini
def predict(self, X):
"""
对输入数据进行预测
参数:
- X: 待预测数据的特征数组。
返回:
- 预测的标签数组。
"""
return np.array([self._predict(inputs) for inputs in X])
def _predict(self, inputs):
"""
递归地预测单个样本的标签
参数:
- inputs: 单个样本的特征数组。
返回:
- 预测的标签。
"""
node = self.tree_
while 'predicted_class' not in node:
feature_value = inputs[node['feature']]
# 根据特征值和阈值判断进入左子树还是右子树
if feature_value < node['threshold']:
node = node['left']
else:
node = node['right']
return node['predicted_class']
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 初始化决策树分类器
clf = DecisionTreeClassifier(max_depth=2)
clf.fit(X_train, y_train)
print("test:"+str(X_test)+"\n pre:"+str(y_test))
print("Predictions:", clf.predict(X_test))
accuracy = accuracy_score(y_test, clf.predict(X_test))
print("准确率:"+str(accuracy*100)+'%')
四、结果
本次实验采用的是python自带的鸢尾花数据集,将数据集8:2分为训练集和测试集,将树的最大深度设置为2,得到的结果如下:
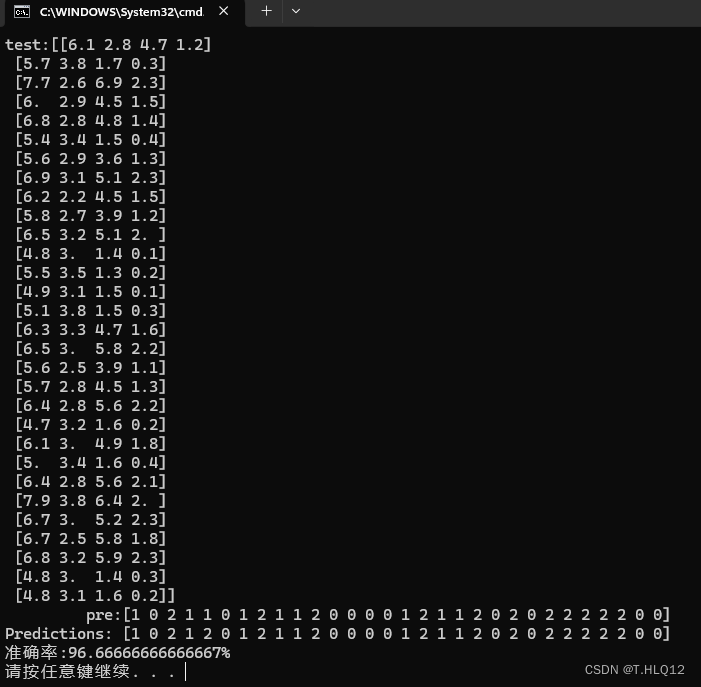
可以看到只有一个点出现了错误,预测的效果不错。
五、问题与解决
问题1.
-
过拟合:决策树容易在训练数据上过拟合,即模型过于复杂,过度拟合训练数据中的噪声或特定样本,导致在测试数据上表现不佳。欠拟合:与过拟合相反,如果决策树过于简单,可能无法捕捉数据中的复杂关系,导致在训练和测试数据上都表现不佳。
-
解决:减缓过拟合:降低模型复杂度、增加训练数据量、使用正则化技术、特征选择等。减缓欠拟合:增加模型复杂度、添加更多特征、使用更复杂的模型等
问题2.
-
内存消耗问题:如果数据集过大或者决策树过深,可能导致内存消耗过大,甚至导致程序崩溃或者运行缓慢。
-
解决:限制最大深度:通过设置决策树的最大深度来限制树的复杂度,从而减少内存消耗。限制叶子节点数量:设置叶子节点的最小样本数,以避免树过于深。使用剪枝:在树的训练过程中或者之后对树进行剪枝,去掉不必要的分支和节点。分批处理数据:将数据集划分为小批次,并逐批进行训练和预测,以减少一次性处理的内存需求。