本系列用于推导、记录该系列视频中本人不熟悉、或认为有价值的知识点
本篇记录第一讲(选修):神奇宝贝分类

如图,为了估算某个样本属于某类的概率,在二分类问题中,我们需要计算红框所示的4个参数,现在进入实例:

如图,我们在ID<400的宝可梦中选出水系和普通系用于训练。首先估计图中所示的2个参数,使用下图右下角红框方法计算即可

现在,为了从训练集中估算出某种测试集中宝可梦出现的机率,需要根据已知的数据估算一个模型,请看图:
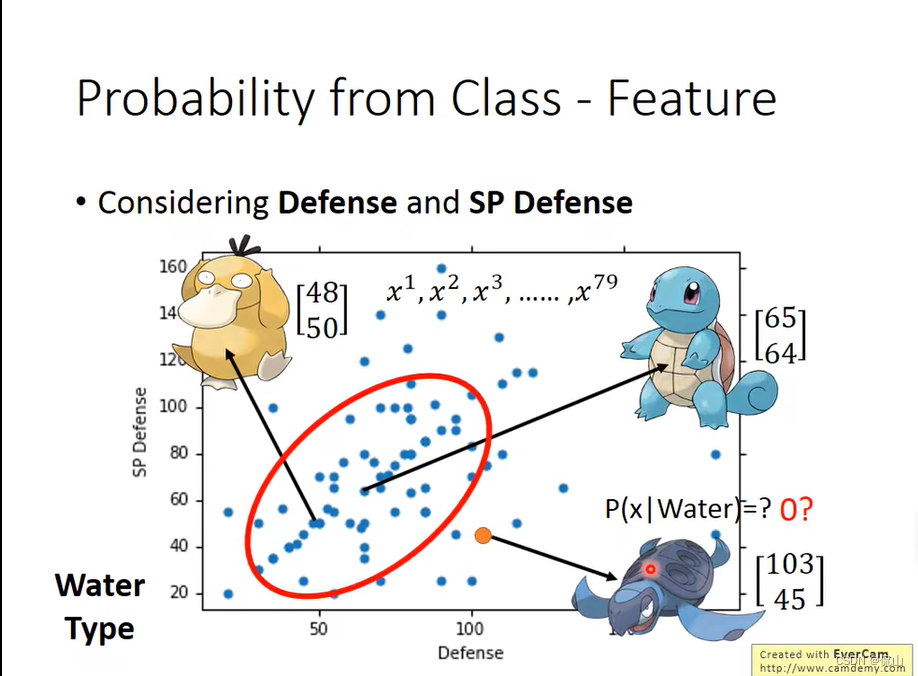
先只考虑二维特征的情况,假设此时水系宝可梦的分布是二维正态分布,我们需要找到使该分布最可能符合上图状况的mean和covariance,如下图所示:
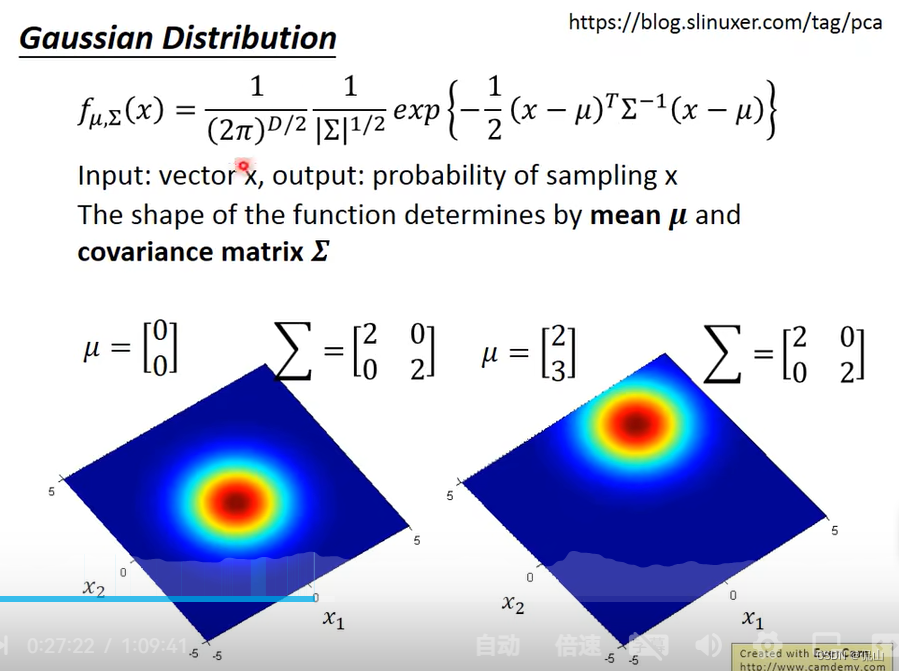
有了这2个参数,我们就可以观察出任意输入被sample出的相对几率大小。
怎么找mean和covariance?用Maximum Likelihood!只需找到对应参数,使似然函数
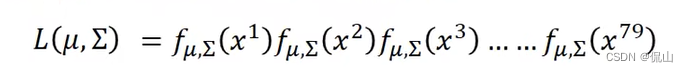
最大即可,具体方法可如下计算:
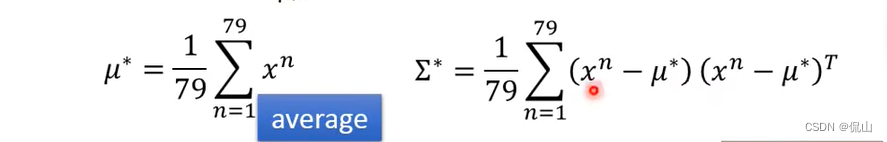
由此,可分别计算出水系和一般系的水平宝贝的参数如下图:
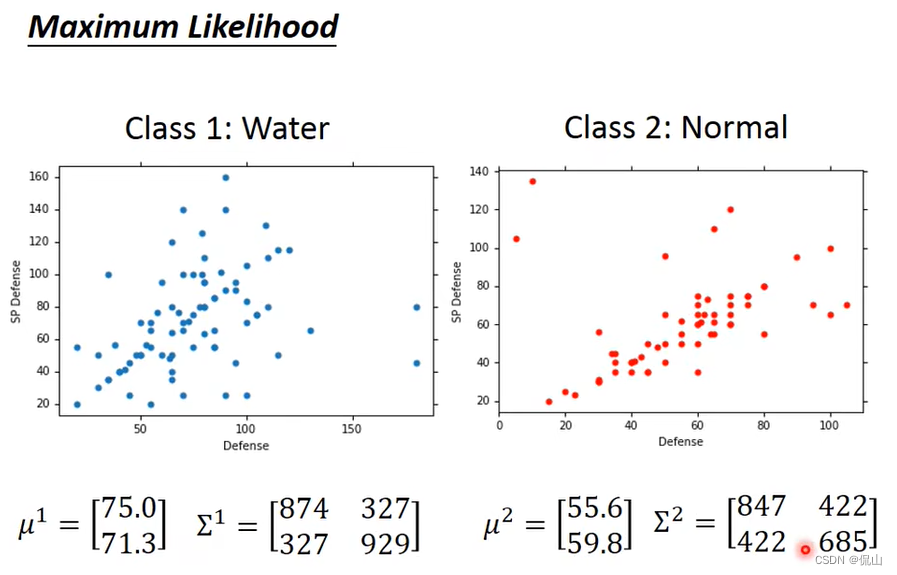
现在,我们终于可以做分类了,计算依据如下:
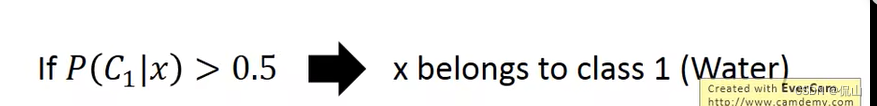
所需的各个参数也都有了:
(尽管用概率分布来算概率不太严谨)
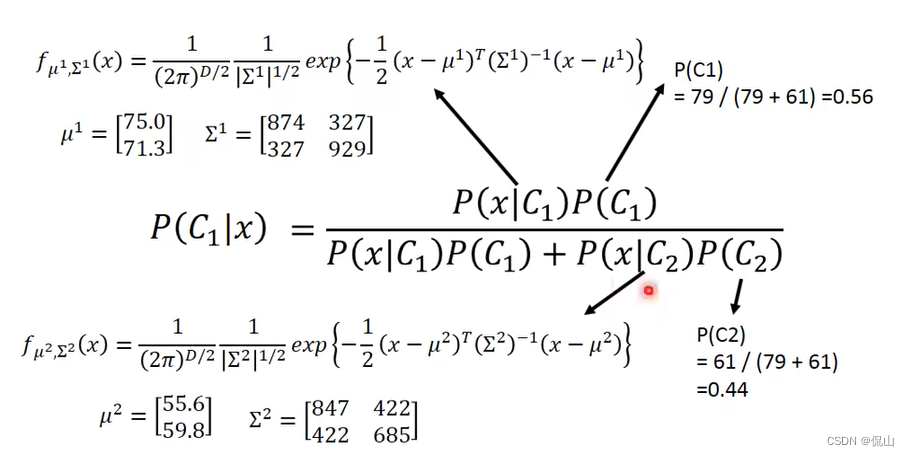
由此,可以绘图如下,根据boundary观察分类效果:
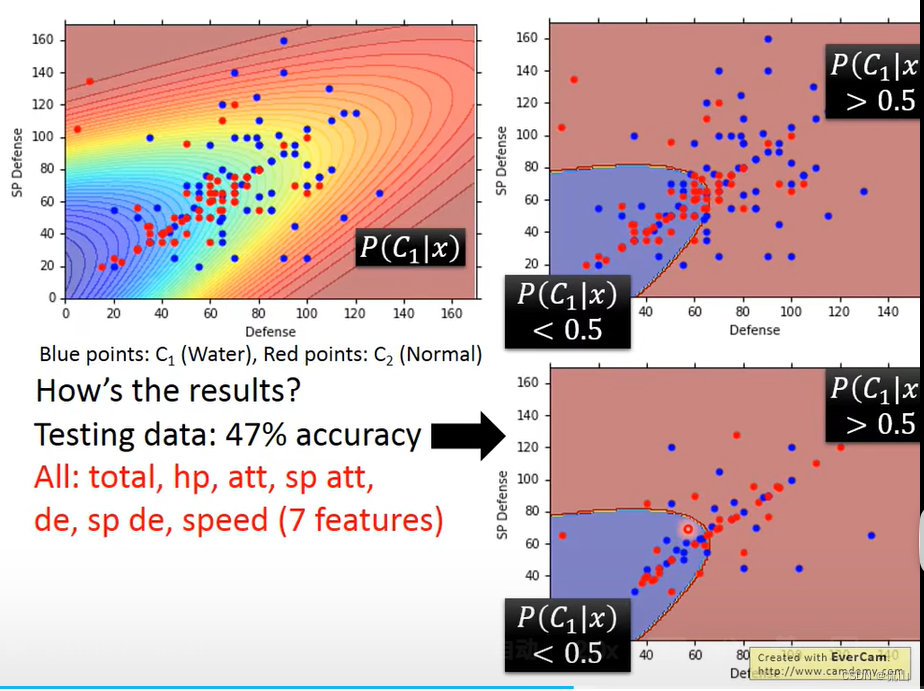
二维空间的表现不太好,也许七维空间会更好?我们用同样方法计算出参数:

但最终表现也不太好……我们应该如何改进?
当维度变为七维时,协方差矩阵很大,参数很多,可能出现过拟合。于是我们把两个协方差矩阵弄成同一个,可以减少49个参数。现在,推导省略,见下图:

有了公共协方差矩阵以后,边界也会变成直线(图放不下了),转个人笔记(2)