在看这一篇文章之前,希望熟悉掌握熵的知识,可看我写的跟熵相关的一篇博客https://blog.csdn.net/m0_59156726/article/details/138128622
1. GAN
原始论文:https://arxiv.org/pdf/1406.2661.pdf
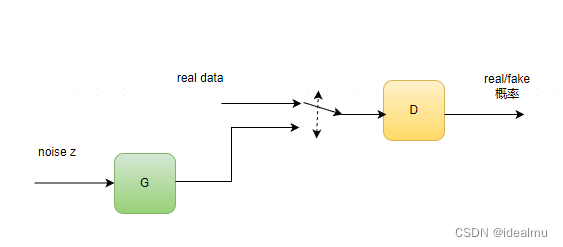
放一张GAN的结构,如下:我们有两个网络,生成网络G和判别网络D。生成网络接收一个(符合简单分布如高斯分布或者均匀分布的)随机噪声输入,通过这个噪声输出图片,记做G(z)。判别网络的输入是x,x代表一张图片,输出D(x)代表x为真实图片的概率。最终的目的式能够生成一个以假乱真的图片,使D无法判别真假,D存在的意义是不断去督促G生成的质量
先拿出论文中的优化公式,后面在详解由来。
m
i
n
G
m
a
x
D
V
(
G
,
D
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
l
o
g
(
1
−
D
(
G
(
z
)
)
)
]
\underset{G}{min} \underset{D}{max}V(G,D) = E_{x\sim p_{data}(x)}[logD(x)] + E_{z\sim p_{z}(z)}[log(1 - D(G(z)))]
GminDmaxV(G,D)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
这里
p
d
a
t
a
(
x
)
p_{data}(x)
pdata(x) 表示真实数据的分布,z是生成器G输入的噪声,
p
z
(
z
)
p_{z}(z)
pz(z)是噪声的分布,乍一看这个公式是不是很难理解。没关系,接下来,我们慢慢分析由来。
2 GAN的优化函数
2.1 判别器D
我们先看判别器D,作用是能够对真实数据
x
∼
p
d
a
t
a
(
x
)
x\sim~p_{data}(x)
x∼ pdata(x)其能够准确分辨是真,对生成的假数据G(z)能够分辨是假,那么实际上这就是一个二分类的逻辑回归问题,还记得交叉熵吗?没错这也等价于交叉熵,只不过交叉熵是负对数,优化最小交叉熵必然等价于优化以下最大值:
m
a
x
D
V
(
G
,
D
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
l
o
g
(
1
−
D
(
G
(
z
)
)
)
]
\underset{D}{max}V(G,D) = E_{x\sim p_{data}(x)}[logD(x)] + E_{z\sim p_{z}(z)}[log(1 - D(G(z)))]
DmaxV(G,D)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
看过我前面写的熵的问题,公式由来很容易懂。我们现在单独从公式来看,这个函数要想取得最大值,必然当真实数据来的时候D(x)=1,当假数据G(z)来的时候D(x)=0。这也满足我们的初衷:能够分辨真假。实际上是一个二分类。
这一步目标是优化D,G是固定的不做优化,G为上一次迭代优化后的结果,因此可简写成:
D
G
∗
=
m
a
x
D
V
(
G
,
D
)
D_G^*= \underset{D}{max}V(G,D)
DG∗=DmaxV(G,D)
2.2 生成器G
在来看看生成器,对于生成器来说,我不想判别器D能够识别我是真假,我希望判别器识别不出来最好,理想极端情况下:D(x)=0,D(G(z))=1,也就是真的识别成假,假的识别成真。反应在优化函数上就是,是不是很好理解了
m
i
n
G
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
l
o
g
(
1
−
D
(
G
(
z
)
)
)
]
\underset{G}{min} = E_{x\sim p_{data}(x)}[logD(x)] + E_{z\sim p_{z}(z)}[log(1 - D(G(z)))]
Gmin=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
当理想情况下D(x)=0,D(G(z))=1,必然是最小值优化。
同样这一步优化是优化G,D不做优化,D为上一次迭代优化后的结果,因此可简写成:
G
D
∗
=
m
i
n
G
V
(
G
,
D
)
G_D^*= \underset{G}{min}V(G,D)
GD∗=GminV(G,D)
2.3 互相博弈
作者习惯上把分开的两个优化写道一起,就变成了我们最初看到的论文中的公式:
m
i
n
G
m
a
x
D
V
(
G
,
D
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
l
o
g
(
1
−
D
(
G
(
z
)
)
)
]
\underset{G}{min} \underset{D}{max}V(G,D) = E_{x\sim p_{data}(x)}[logD(x)] + E_{z\sim p_{z}(z)}[log(1 - D(G(z)))]
GminDmaxV(G,D)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
但是实际上,D和G在迭代过程中是分开优化的。
上面说了,我生成器又要能够准确判断真假,又要不能够判断,作为判别器他说他好难啊,怎么办呢,干脆判别器最终输出0.5,这也是理想优化结果,谁也不偏向。这也是整个GAN优化的终极目的。
3 训练过程

对于判别器D优化,因为这是个二分类,ylogq + (1-y)log(1-q):对于x,标签只会为1,因此只有log(D(x))这一项;对于g(z),其标签只会为0,因此只有log(1-D(G(z)))这一项,在损失函数上,
l
o
s
s
=
c
r
o
s
s
E
n
t
r
y
L
o
s
s
(
1
,
D
(
x
)
)
+
c
r
o
s
s
E
n
t
r
y
L
o
s
s
(
0
,
D
(
G
(
z
)
)
)
loss=crossEntryLoss(1,D(x)) + crossEntryLoss(0,D(G(z)))
loss=crossEntryLoss(1,D(x))+crossEntryLoss(0,D(G(z)))
对于生成器G优化:因为D(x)这一项,并不包含生成器的优化参数,因此在求梯度的时候D(x)这一项为0,因此只有log(1-D(G(z)))这一项,损失函数:
l
o
s
s
=
c
r
o
s
s
E
n
t
r
y
L
o
s
s
(
1
,
D
(
G
(
z
)
)
)
loss=crossEntryLoss(1,D(G(z)))
loss=crossEntryLoss(1,D(G(z)))
4 在看优化
4.1 D的最优解
还记得完美的优化结果是D=0.5吗?这到底是怎么来的呢。我们先看一下对于D的优化,去求D的最优解
m
a
x
D
V
(
G
,
D
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
l
o
g
(
1
−
D
(
G
(
z
)
)
)
]
\underset{D}{max}V(G,D) = E_{x\sim p_{data}(x)}[logD(x)] + E_{z\sim p_{z}(z)}[log(1 - D(G(z)))]
DmaxV(G,D)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
写成积分形式:不知道怎么来的可以补一下概率论均值的计算。
m
a
x
D
V
(
G
,
D
)
=
∫
x
p
d
a
t
a
(
x
)
l
o
g
D
(
x
)
d
x
+
∫
x
p
z
(
z
)
l
o
g
(
1
−
D
(
g
(
z
)
)
)
d
z
\underset{D}{max}V(G,D) = \int_{x}p_{data}(x)logD(x)dx + \int_{x}p_{z}(z)log(1-D(g(z)))dz
DmaxV(G,D)=∫xpdata(x)logD(x)dx+∫xpz(z)log(1−D(g(z)))dz
我们考虑在优化D的时候G是不变的,并且假设,通过G生成的g(z)满足的分布为
p
g
p_g
pg,因此上式子可写为:
m
a
x
D
V
(
G
,
D
)
=
∫
x
p
d
a
t
a
(
x
)
l
o
g
D
(
x
)
+
p
g
(
x
)
l
o
g
(
1
−
D
(
x
)
d
x
\underset{D}{max}V(G,D) = \int_{x}p_{data}(x)logD(x) + p_{g}(x)log(1-D(x)dx
DmaxV(G,D)=∫xpdata(x)logD(x)+pg(x)log(1−D(x)dx
上式什么时候取得最大结果呢,
a
l
o
g
(
y
)
+
b
l
o
g
(
1
−
y
)
alog(y) + blog(1-y)
alog(y)+blog(1−y)在[0,1]上最大值是y=a/(a+b),因此上式最大值是
D
G
∗
(
x
)
=
p
d
a
t
a
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
D_G^*(x)= \cfrac{p_{data}(x)}{p_{data}(x)+p_g(x)}
DG∗(x)=pdata(x)+pg(x)pdata(x)
以上我们得到D的最优解,但是别忘了,我们目标是G能够生成的分布pg能和pdata一致,让D真假难辨,那么此时pg = pdata,D=0.5,判别器已经模棱两可了。然而这一结果只是我们的猜测。
4.2 G的最优解
作者也是先说了pg=pdata是G的最优解,后面才证明的。让我们跟着作者思路证明一下。
D的最优解已经得到了,带入求解G最优的公式,这里作者起了个C(G)的名称,按照他的思路来,已然求C(G)的最小值
C
(
G
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
G
∗
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
l
o
g
(
1
−
D
G
∗
(
G
(
z
)
)
)
]
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
D
G
∗
(
x
)
]
+
E
x
∼
p
g
[
l
o
g
(
1
−
D
G
∗
(
x
)
)
]
=
E
x
∼
p
d
a
t
a
(
x
)
[
l
o
g
p
d
a
t
a
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
]
+
E
x
∼
p
g
[
l
o
g
(
p
g
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
)
]
=
∫
x
p
d
a
t
a
(
x
)
l
o
g
p
d
a
t
a
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
+
p
g
(
x
)
l
o
g
p
g
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
d
x
=
∫
x
(
l
o
g
2
−
l
o
g
2
)
p
d
a
t
a
(
x
)
+
(
l
o
g
2
−
l
o
g
2
)
p
g
(
x
)
+
p
d
a
t
a
(
x
)
l
o
g
p
d
a
t
a
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
+
p
g
(
x
)
l
o
g
p
g
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
d
x
=
−
l
o
g
2
∫
x
[
p
d
a
t
a
(
x
)
+
p
g
(
x
)
]
d
x
+
∫
x
p
d
a
t
a
(
x
)
(
l
o
g
2
+
l
o
g
p
d
a
t
a
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
)
+
p
g
(
x
)
(
l
o
g
2
+
l
o
g
p
g
(
x
)
p
d
a
t
a
(
x
)
+
p
g
(
x
)
)
d
x
C(G) = E_{x\sim p_{data}(x)}[logD_G^*(x)] + E_{z\sim p_{z}(z)}[log(1 - D_G^*(G(z)))] \\ =E_{x\sim p_{data}(x)}[logD_G^*(x)] + E_{x\sim p_{g}}[log(1 - D_G^*(x))] \\ =E_{x\sim p_{data}(x)}[log\cfrac{p_{data}(x)}{p_{data}(x)+p_g(x)} ] + E_{x\sim p_{g}}[log(\cfrac{p_{g}(x)}{p_{data}(x)+p_g(x)} )]\\ = \int_{x}p_{data}(x)log\cfrac{p_{data}(x)}{p_{data}(x)+p_g(x)} + p_{g}(x)log\cfrac{p_g(x)}{p_{data}(x)+p_g(x)}dx\\ = \int_{x}(log2-log2)p_{data}(x) + (log2-log2)p_{g}(x) + p_{data}(x)log\cfrac{p_{data}(x)}{p_{data}(x)+p_g(x)} + p_{g}(x)log\cfrac{p_g(x)}{p_{data}(x)+p_g(x)}dx\\ =-log2\int_{x}[p_{data}(x)+p_g(x)]dx + \int_{x}p_{data}(x)(log2 +log \cfrac{p_{data}(x)}{p_{data}(x)+p_g(x)}) + p_{g}(x)(log2 + log\cfrac{p_{g}(x)}{p_{data}(x)+p_g(x)})dx
C(G)=Ex∼pdata(x)[logDG∗(x)]+Ez∼pz(z)[log(1−DG∗(G(z)))]=Ex∼pdata(x)[logDG∗(x)]+Ex∼pg[log(1−DG∗(x))]=Ex∼pdata(x)[logpdata(x)+pg(x)pdata(x)]+Ex∼pg[log(pdata(x)+pg(x)pg(x))]=∫xpdata(x)logpdata(x)+pg(x)pdata(x)+pg(x)logpdata(x)+pg(x)pg(x)dx=∫x(log2−log2)pdata(x)+(log2−log2)pg(x)+pdata(x)logpdata(x)+pg(x)pdata(x)+pg(x)logpdata(x)+pg(x)pg(x)dx=−log2∫x[pdata(x)+pg(x)]dx+∫xpdata(x)(log2+logpdata(x)+pg(x)pdata(x))+pg(x)(log2+logpdata(x)+pg(x)pg(x))dx
由于对概率积分结果为1,上式继续化简为:
C
(
G
)
=
−
2
l
o
g
2
+
∫
x
p
d
a
t
a
(
x
)
l
o
g
p
d
a
t
a
(
x
)
[
p
d
a
t
a
(
x
)
+
p
g
(
x
)
]
/
2
+
∫
x
p
g
(
x
)
l
o
g
p
g
(
x
)
[
p
d
a
t
a
(
x
)
+
p
g
(
x
)
]
/
2
C(G)=-2log2 + \int_{x}p_{data}(x)log\cfrac{p_{data}(x)}{[p_{data}(x)+p_g(x)]/2} + \int_{x}p_{g}(x)log\cfrac{p_{g}(x)}{[p_{data}(x)+p_g(x)]/2}
C(G)=−2log2+∫xpdata(x)log[pdata(x)+pg(x)]/2pdata(x)+∫xpg(x)log[pdata(x)+pg(x)]/2pg(x)
看过熵的应该知道后两项其实式散度的形式,写为散度的形式,
C
(
G
)
=
−
l
o
g
4
+
K
L
(
p
d
a
t
a
(
x
)
∣
∣
p
d
a
t
a
(
x
)
+
p
g
(
x
)
2
)
+
K
L
(
p
g
(
x
)
∣
∣
p
d
a
t
a
(
x
)
+
p
g
(
x
)
2
)
C(G)=-log4 + KL(p_{data}(x)||\cfrac{p_{data}(x)+p_g(x)}{2})+KL(p_{g}(x)||\cfrac{p_{data}(x)+p_g(x)}{2})
C(G)=−log4+KL(pdata(x)∣∣2pdata(x)+pg(x))+KL(pg(x)∣∣2pdata(x)+pg(x))
在我写熵的那篇文章里已经详细介绍和推导过,KL(P||Q)散度取最小值0的时候P=Q,因此上式最小值的情况是:
p
d
a
t
a
(
x
)
=
p
d
a
t
a
(
x
)
+
p
g
(
x
)
2
p_{data}(x) = \cfrac{p_{data}(x)+p_g(x)}{2}
pdata(x)=2pdata(x)+pg(x) 和
p
g
(
x
)
=
p
d
a
t
a
(
x
)
+
p
g
(
x
)
2
p_{g}(x) = \cfrac{p_{data}(x)+p_g(x)}{2}
pg(x)=2pdata(x)+pg(x)。这两个当且仅当
p
g
(
x
)
=
p
d
a
t
a
(
x
)
p_{g}(x)=p_{data}(x)
pg(x)=pdata(x)时满足。
又因为JSD散度和KL散度有如下关系:
J
S
D
(
P
∣
∣
Q
)
=
1
2
K
L
(
P
∣
∣
M
)
+
1
2
K
L
(
Q
∣
∣
M
)
,
M
=
1
2
(
P
+
Q
)
JSD(P||Q) = \cfrac{1}{2}KL(P||M)+\cfrac{1}{2}KL(Q||M),M= \cfrac{1}{2}(P+Q)
JSD(P∣∣Q)=21KL(P∣∣M)+21KL(Q∣∣M),M=21(P+Q)
因此继续简化:
C
(
G
)
=
−
l
o
g
4
+
2
J
S
D
(
p
d
a
t
a
∣
∣
p
g
)
C(G)=-log4+2JSD(p_{data}||p_g)
C(G)=−log4+2JSD(pdata∣∣pg)
由于JSD的散度取值为(0,log2),当为0的时候
p
g
=
p
d
a
t
a
p_{g}=p_{data}
pg=pdata,同样也证明了G最优解的情况是
p
g
=
p
d
a
t
a
p_{g}=p_{data}
pg=pdata。至此也完成论文中的证明,不得不说GAN中的理论真的很强,这些理论对后面各种生成模型用处非常大。虽然GAN是历史的产物,但是他带来的价值却很高,如果想做AIGC,GAN必学习。
备注
参考:
https://blog.csdn.net/sallyxyl1993/article/details/64123922
https://www.cnblogs.com/LXP-Never/p/9706790.html