机器学习/算法工程师面试题目与答案-深度学习部分1

机器学习/算法工程师面试题目与答案-深度学习部分

- - BatchNormalization的作用
  - 梯度消失
  - 循环神经网络，为什么好?
  - 什么是GroupConvolution
  - 什么是RNN
  - 神经网络中权重共享的是？
  - 神经网络激活函数？
  - 为什么在深度学习中常进行finetuning
  - 画GRU结构图
  - 什么是dropout
  - LSTM每个门的计算公式
  - HOG算法原理
  - HOG算子是怎么求梯度的
  - DropConnect的原理
  - 介绍一下GMM-HMM
  - Pytorch

BatchNormalization的作用

BatchNormalization (BN) 主要用来解决深度神经网络训练过程中的内部协变量偏移问题，通过对每一层输入进行归一化处理，使得各层的学习更加独立高效。BN还有助于缓解梯度消失问题，可以使用更高的学习率，加速模型收敛。

梯度消失

在深度神经网络中，梯度消失是指在反向传播过程中，梯度随着层数增加而逐渐变小，导致网络深层部分权重更新非常缓慢，从而使得训练效率低下。通常由于使用了如Sigmoid或Tanh这类导数值容易饱和的激活函数引起。

循环神经网络，为什么好?

循环神经网络（RNNs）具有以下主要优点，使其在处理序列数据方面表现出色：

时间依赖性：RNN 能有效处理和预测序列中数据点的时间关系，适用于语音识别、语言建模等任务。
可变长度输入：RNN 可处理不同长度的输入序列，适合自然语言处理等领域。
参数共享：通过在序列的每个时间步使用相同的权重，RNN 减少了总参数数量，提高了泛化能力。
上下文信息利用：RNN 能够利用前面的输入信息来影响后续的输出，对于需要考虑整个输入历史的任务（如机器翻译）非常有效。
然而，RNN也存在梯度消失或爆炸的问题，影响训练的稳定性和效率。为改善这些问题，已发展出LSTM和GRU等更高级的变体

什么是GroupConvolution

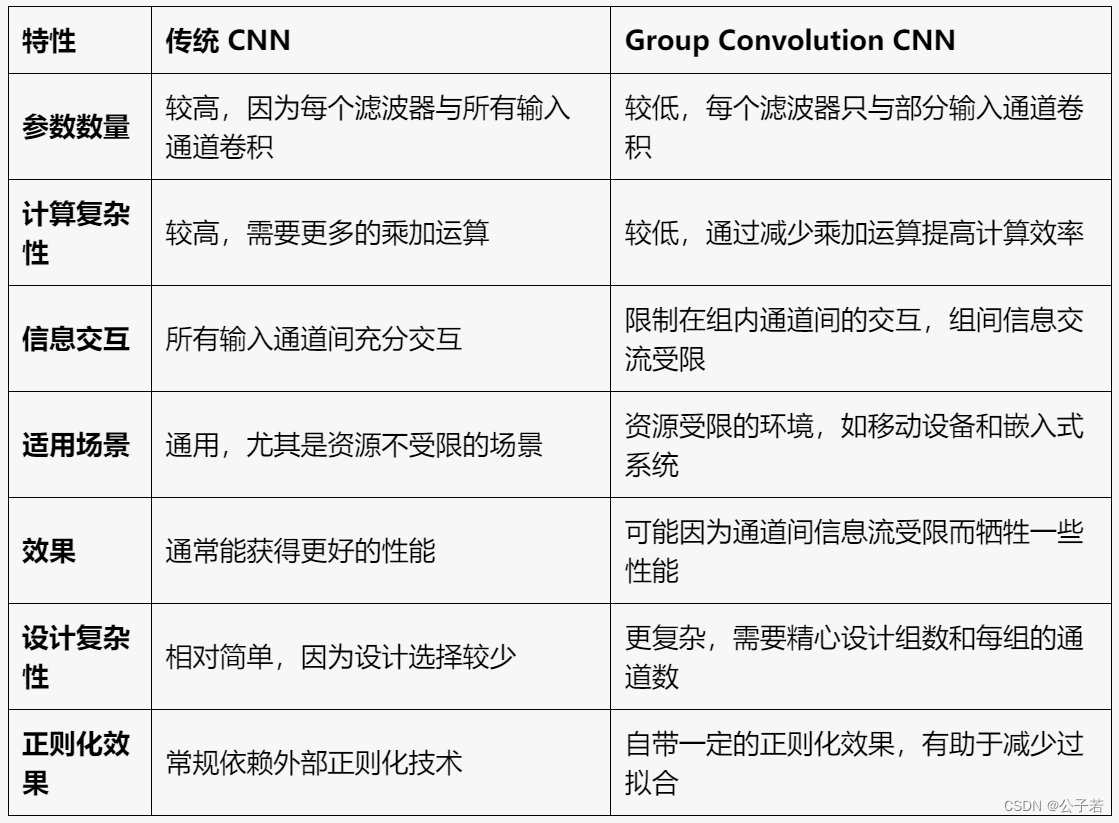
Group convolution是卷积神经网络中一种特殊的卷积方式，它将输入的特征图分成若干组，每组独立进行卷积操作。这种方法可以减少参数数量，降低计算复杂度，同时增强网络的表达能力。

主要特点：
参数减少：每个滤波器只处理部分输入通道，减少了总参数量。
计算效率提高：通过减少乘加操作，提升计算效率。
正则化效果：增加模型的正则化，有助于减少过拟合。
缺点：
信息流受限：限制了不同组间的信息交流，可能影响特征捕捉能力。
设计复杂性：需要适当选择组数，增加设计难度。

什么是RNN

RNN（Recurrent Neural Network）是一类用于处理序列数据的神经网络，它通过将前一时间步的隐藏状态传递到当前时间步，从而能够维持一定的记忆性。

主要特点：
处理时间序列：能够处理和记忆输入序列中的时间动态。
参数共享：在序列的每一个时间步中重复使用相同的权重，减少模型复杂性。
灵活的输入长度：可以接收不同长度的输入序列。
工作原理：
在每个时间步，RNN接收当前输入和上一时间步的隐状态，更新当前的隐状态，并可能产生一个输出。
挑战：
梯度消失和爆炸：在长序列中训练时可能面临梯度消失或爆炸的问题。
计算效率：由于序列依赖性，难以并行处理序列数据。
为了克服这些挑战，更先进的变体如LSTM（长短期记忆）和GRU（门控循环单元）被开发出来，它们通过引入门控机制改善了长期依赖的学习能力和稳定性。

### 模型不收敛的原因训练过程中,若一个模型不收敛,那么是否说明这个模型无效?导致模型不收敛的原因有哪些? 模型不收敛并不一定意味着模型无效。可能的原因包括学习率设置不当、数据预处理错误、模型结构不适合处理特定的数据类型、过拟合或欠拟合等。调整这些因素可能帮助模型收敛。 ### 图像处理中锐化和平滑的操作锐化是通过增强图像的边缘和细节来使图像看起来更清晰，常用的方法包括使用拉普拉斯算子。平滑（或模糊）操作通过减少图像的高频成分来降低噪声和细节，常用的方法有均值滤波、高斯滤波等 ### VGG使用3*3卷积核的优势是什么? 3x3是最小尺寸的卷积核可以捕捉像素间的空间关系，多个3x3卷积层叠加可以等效于更大的感受野（例如两个3x3卷积层叠加相当于一个5x5卷积核的效果），同时参数更少、计算效率更高。 ### Relu比Sigmoid的效果好在哪里? Relu（线性整流函数）比Sigmoid函数在深层网络中效果好，主要因为它解决了梯度消失问题，且计算上更简单高效。 - 解决梯度消失问题 Sigmoid 函数的输出范围是 (0, 1)，在输入值非常大或非常小的时候，Sigmoid函数的梯度接近于0，这会导致梯度消失问题，使得网络深层中的权重难以更新。 ReLU 函数在正数部分的梯度恒为1，因此在正输入值的情况下不会发生梯度消失问题，有助于在训练深层网络时保持较好的梯度流。

神经网络中权重共享的是？

权重共享主要用于卷积神经网络中，同一卷积核在整个输入特征图上滑动计算，这样可以显著减少模型的参数数量，降低过拟合风险，同时提高计算效率。

神经网络激活函数？

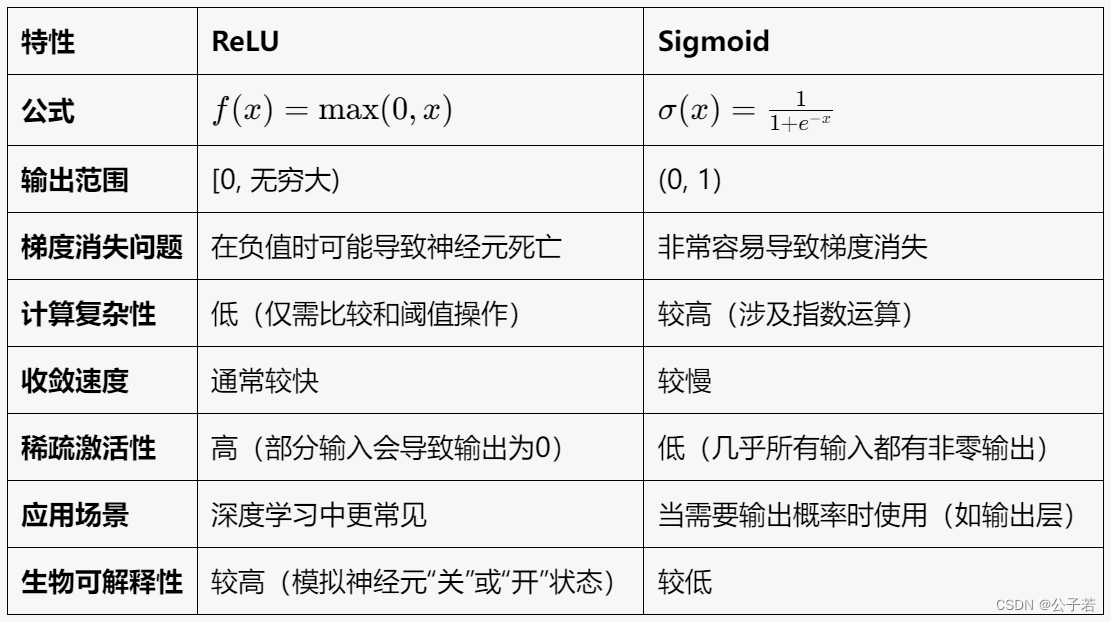
激活函数在神经网络中用于添加非线性决策边界，使得网络可以学习更复杂的模式。常见的激活函数包括ReLU、Sigmoid、Tanh等。

为什么在深度学习中常进行finetuning

在深度学习中，通常会finetuning已有的成熟模型，再基于新数据，修改最后几层神经网络权值，为什么？
Finetuning允许模型在一个已经预训练好的基础上，针对新的特定任务进行调整。这样可以利用预训练模型在大量数据上学到的通用特征，只需少量数据就能达到较好的性能。

画GRU结构图

GRU（Gated Recurrent Unit）结构包括重置门和更新门，具体结构图涉及输入、隐藏状态和门控制的交互。 ### Attention机制的作用 Attention机制可以使模型在处理信息时更加聚焦于重要的部分，提高模型的解析能力，常见于NLP和图像处理领域，如机器翻译的Transformer模型。 ### Lstm和Gru的原理 LSTM（Long Short-Term Memory）通过引入遗忘门、输入门和输出门来控制信息的保留与遗忘，解决长序列数据的依赖问题。GRU是LSTM的变种，结构更简单，只有两个门（更新门和重置门），计算效率更高，但在某些任务上可能不如LSTM强大。

什么是dropout

Dropout是一种正则化技术，通过在训练过程中随机“丢弃”一部分神经网络的节点，来防止模型过拟合。
（Dropout 是一种技巧，用于帮助神经网络避免过于依赖训练数据中的特定模式，从而防止过拟合。想象一下，你在组装一个团队来解决问题，但为了确保团队不过分依赖某个关键成员，你决定在每次讨论时随机让一些成员休息。这样，整个团队就会学习如何在不完全的情况下也能找到解决方案，使得团队整体更加灵活和强大。

在神经网络中，Dropout 的做法类似于这种随机让一些“团队成员”（神经元）休息的策略。在模型训练的每一步中，每个神经元都有一定的概率被“关闭”，不参与这一次的学习过程。这样一来，网络就不能依赖于任何单个神经元，而是必须寻找更多的可能性来得出正确的输出。

训练完成后，在实际使用模型时，所有的神经元都会被启用，但它们的输出会根据之前的丢弃概率进行调整，以确保模型表现的一致性。这种方法简单而有效，广泛用于提高各种神经网络的性能和稳定性。）

LSTM每个门的计算公式

Input Gate:
$i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi})$

Forget Gate:
$f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf})$

Candidate Cell State:
$\tilde{C}_t = \tanh(W_{ic} x_t + b_{ic} + W_{hc} h_{t-1} + b_{hc})$

Cell State Update:
$C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$

Output Gate:
$o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho})$

Hidden State:
$h_t = o_t \odot \tanh(C_t)$

公式内的变量如 $W$ , $b$ , $x_t$ , $h_{t-1}$ , 和 $C_{t-1}$ 分别代表权重矩阵、偏置项、当前输入、前一时间步的隐藏状态和细胞状态。

HOG算法原理

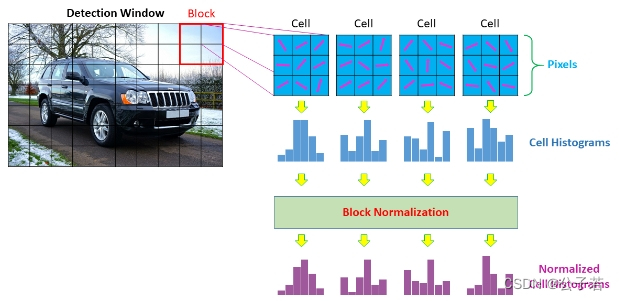
HOG（Histogram of Oriented Gradients）算法主要通过计算图像局部区域内的梯度方向直方图来描述这些区域的外观和形状，广泛用于图像中的物体检测。
HOG算法的基本步骤包括：

归一化颜色和伽马校正：为了减少图像光照变化的影响，通常先对图像进行颜色归一化或进行伽马校正。
计算梯度：计算图像每个像素的梯度（大小和方向）。梯度方向代表了图像的边缘方向，而大小给出了边缘的强度。
单元划分：将图像划分为小的连接区域，称为单元（cells）。每个单元通常是6x6或8x8的像素块。
计算直方图：在每个单元中，根据梯度方向将梯度大小累积到一个方向直方图中。例如，可以使用9个方向的直方图（0-180度，每20度一个桶）。
块归一化：为了进一步降低光照的影响，通常需要对相邻的单元组成的更大的区域（称为块）进行局部归一化。每个块可以包含2x2个单元，并且块与块之间可以有重叠。归一化可以基于L2范数、L1范数或其他规则。
特征描述符构建：将所有的块描述符串联起来形成最终的特征向量，用于后续的学习和分类任务。

HOG算子是怎么求梯度的

在HOG（Histogram of Oriented Gradients）算法中，计算图像梯度是一个关键步骤。图像梯度计算可以通过以下差分公式完成：

$G_x = I(x+1, y) - I(x-1, y)$
$G_y = I(x, y+1) - I(x, y-1)$
其中， $G_x$ 和 $G_y$ 分别表示水平和垂直方向上的梯度， $I (x, y)$ 是图像在位置 $(x, y)$ 的像素值。
接下来，我们可以计算每个像素的梯度大小和方向：
Magnitude = $\sqrt{G_x^2 + G_y^2}$
Angle = $\tan^{-1}\left(\frac{G_y}{G_x}\right)$
这里， $tan^{-1}$ 表示反正切函数，用于计算梯度的方向。这两个结果（大小和方向）随后用于构建方向梯度直方图，这是HOG特征描述符的核心部分。

DropConnect的原理

具体来说，对于网络中的每个权重，都有一定概率 𝑝 将其临时置为零，而剩下的权重则保持不变。这样，每次前向传播时，网络的结构都会略有不同，这有助于模拟出训练多个不同网络的效果，并通过平均它们的预测来减少过拟合。

与 Dropout 的对比
DropConnect 可以视为 Dropout 的一个一般化形式：
Dropout 随机地将整个神经元（包括其所有输出连接）的输出置为零。
DropConnect 则是随机选择单个权重并将其置为零。
这意味着 DropConnect 在理论上提供了更高的模型复杂度和更细粒度的网络结构调整，因为它可以独立地断开任何单个连接，而不是整个神经元的所有输出。
实践:
DropConnect 的实现涉及以下步骤：
1.权重掩蔽：对于神经网络中的每层，生成一个与权重矩阵同形状的随机矩阵。矩阵中的每个元素都是独立抽取的，根据预设的保持概率 1−p（p是丢弃概率）来决定元素是 0 还是 1。
2.应用掩蔽：在每次前向传播过程中，将生成的掩蔽矩阵与权重矩阵进行元素乘法（Hadamard 乘积）。这样，一部分权重会临时变为零。
3.训练和反向传播：网络如常进行前向传播、损失计算及反向传播。在反向传播过程中，只更新那些在前向传播中未被置零的权重。

介绍一下GMM-HMM

GMM-HMM模型
在GMM-HMM模型中，HMM用于建模时间序列数据中的状态转移，而GMM用于建模在给定状态下的观测数据的概率分布。具体来说：

HMM负责模型的时间依赖性：它允许我们建模序列中隐状态的转移。
GMM负责建模观测数据的复杂分布：在传统的HMM中，每个状态通常与一个简单的概率分布（如高斯分布）相关联。在GMM-HMM中，每个状态的观测概率是由多个高斯分布的混合来描述的，增加了模型描述数据的灵活性。

应用：语音识别
在语音识别中，GMM-HMM非常流行。HMM用于建模语音信号的时间序列特性（例如，语音单元的开始和结束），而GMM用于建模在这些语音单元中观察到的声学信号的概率分布。每个HMM状态可以对应于声音的一部分（如音素），而GMM则负责精确地建模这些音素的声学特征。
训练方法
GMM-HMM模型通常使用EM算法（期望最大化算法）进行参数估计。在语音识别的场景中，还会使用诸如Baum-Welch算法（一种特殊的EM算法，用于HMM）来调整模型参数，使其更好地拟合训练数据。

总结而言，GMM-HMM是一个强大的模型，能够有效地结合序列数据中的时间依赖性和观测数据的复杂统计特性，这使得其在多个领域内都有着广泛的应用。

Pytorch

整体架构说一下，新加一个层需要哪些步骤，卷积是怎么实现的，多卡机制，数据并行还是模型并行？

PyTorch 整体架构概览
PyTorch 是一个以张量（tensor）和动态计算图（autograd system）为核心的深度学习框架，主要包括以下几个组件：

Tensor: PyTorch 的基本数据结构，类似于 NumPy 的 ndarray，但可以在 GPU 上运行以加速计算。
Autograd: 自动微分系统，用于自动计算梯度，核心是 torch.autograd。
nn Module: 提供神经网络层的实现，例如 torch.nn.Linear，torch.nn.Conv2d 等。
Optimizers: 提供优化算法，如 SGD, Adam 等，位于 torch.optim。
Utilities: 如数据加载和处理工具（torch.utils.data）等。

添加新的层
要在 PyTorch 中添加自定义层，您需要定义一个继承自 torch.nn.Module 的类。这通常涉及以下步骤：

定义类：创建一个新的类，继承自 torch.nn.Module。
初始化函数：在 init 方法中初始化层的参数。
前向传播函数：实现 forward 方法，定义层在进行前向传播时的计算逻辑。
例如，创建一个简单的全连接层：

import torch.nn as nn
import torch

class CustomLinear(nn.Module):
    def __init__(self, input_features, output_features):
        super(CustomLinear, self).__init__()
        self.weights = nn.Parameter(torch.randn(input_features, output_features))
        self.bias = nn.Parameter(torch.randn(output_features))

    def forward(self, x):
        return x @ self.weights + self.bias

卷积的实现
在 PyTorch 中，卷积层主要通过 torch.nn.Conv2d 实现。该层在内部使用高效的库（如 cuDNN 或 Intel MKL），这些库对卷积算法进行了高度优化。实际的卷积操作可以视为输入特征图和一组可学习的滤波器之间的滑动窗口运算。
多卡机制
PyTorch 支持数据并行和模型并行两种方式来使用多个 GPU。

数据并行（Data Parallelism）：这是最常见的并行处理形式，将数据分批处理到多个 GPU 上，每个 GPU 计算模型的一个子集，然后合并结果。这可以通过 torch.nn.DataParallel 或 torch.nn.parallel.DistributedDataParallel 实现。
示例使用 DataParallel:

model = models.resnet50()
if torch.cuda.device_count() > 1:
    model = nn.DataParallel(model)
model.to(device)

模型并行（Model Parallelism）：当模型太大而无法在一个 GPU 上完全放下时使用。这种方法涉及到在不同的 GPU 上运行模型的不同部分。用户需要手动指定每个模型部分的 GPU。

示例模型并行:

class ModelParallel(nn.Module):
    def __init__(self, device0, device1):
        super(ModelParallel, self).__init__()
        self.layer1 = nn.Linear(10, 10).to(device0)
        self.layer2 = nn.Linear(10, 5).to(device1)

    def forward(self, x):
        x = self.layer1(x)
        x = x.to(device1)
        return self.layer2(x)