1、向量是什么
1.1、向量的定义
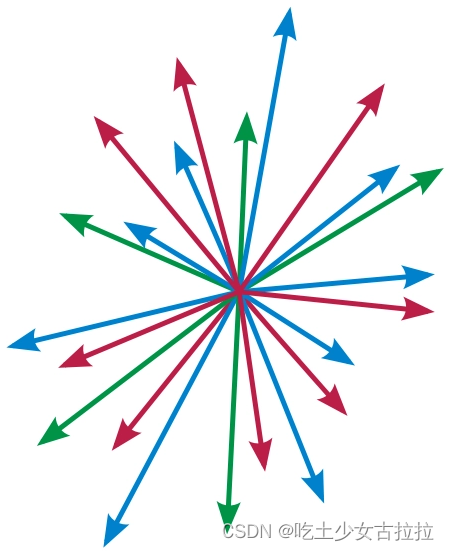
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
1.2、向量的表示
向量的记法:印刷体记作粗体的字母(如a,b,u,v),书写时在字母顶上加一小箭头’‘→’'。如果给定向量的起点(A)和终点(B),可将向量记作
AB
。实际上向量有多种记法,可以用元组表示一个向量,如 (x1,x2 )
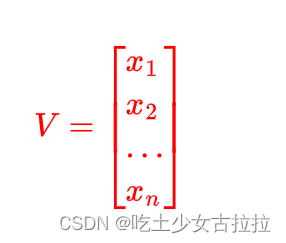
。在线性代数中,n元向量可以用n×1矩阵表示,如:
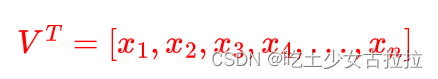
向量中的每个元素 x,都称作向量的一个分量。
1.3、向量物理意义
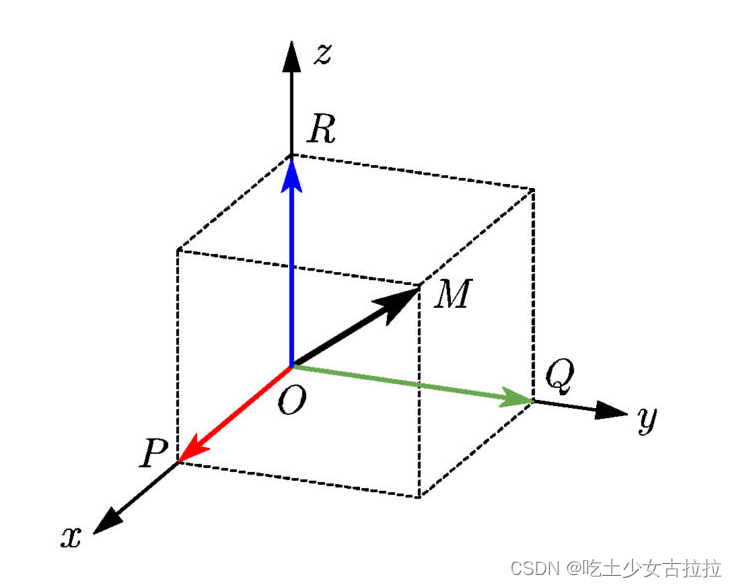

向量的几何意义就是空间中的点,物理意义就是速度或者力这样的矢量。
向量的分量我们称之为维度,n 维向量集合的全体就构成了 n 维欧式空间,一个 n 维向量其实就是一个 n 维欧式空间的一个点。
2、行向量与列向量
行向量在线性代数中,是一个 1×n 的矩阵,即矩阵由一个含有 n 个元素的行所组成即行向量。行向量的转置是一个列向量,反之亦然。
行向量示例:
在线性代数中,列向量是一个 n×1 的矩阵,即矩阵由一个含有 n 个元素的列所组成。
列向量示例:
为简化书写、方便排版起见,有时会以加上转置符号 T 的行向量表示列向量。

在机器学习中说道向量一般都是指列向量。
3、向量运算
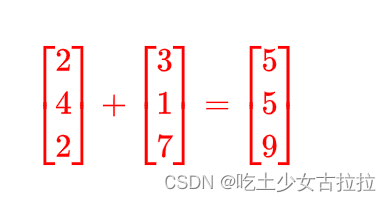
3.1、向量加减法
等于它们的分量分别相加,显然两个向量的长度得是相等的,减法我们在这里不列举,很容易举一反三。
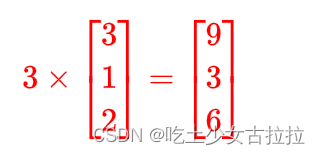
3.2、向量数乘
3.3、转置

3.4、向量内积
两个列向量, ATB,等于对应位置相乘再相加。

3.5、向量运算法则
1、实数与向量运算法则,设λ,μ 是实数,则有:
结合律:λ(μA)=(λμ)A
分配律:(λ+μ)A=λA+μA , λ(A+B)=λA+λB
2、向量内积运算法则
交换律:A⋅B=B⋅A
分配律:(A+B)⋅C=A⋅C+B⋅C
结合律:(λA)⋅B=λ(A⋅B)
4、向量的范数
范数的公式是向量每个分量绝对值 P 次方 再用幂函数计算 P 分之一,这里 P 肯定是整数 1,2,3…到正无穷都是
可以的。向量的范数就是把向量变成一个标量,范数的表示就是两个竖线来表示,然后右下角写上 P。
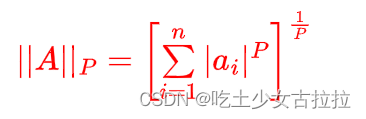
1-范数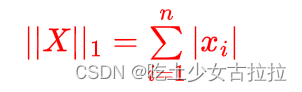
2-范数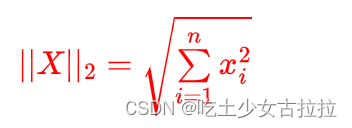
即向量元素的平方和再开方,也叫欧几里得范数,常用计算向量长度,表示 X 到零点的欧式距离。
P-范数
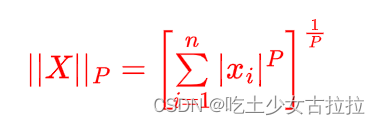
∞-范数
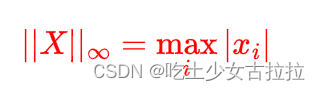
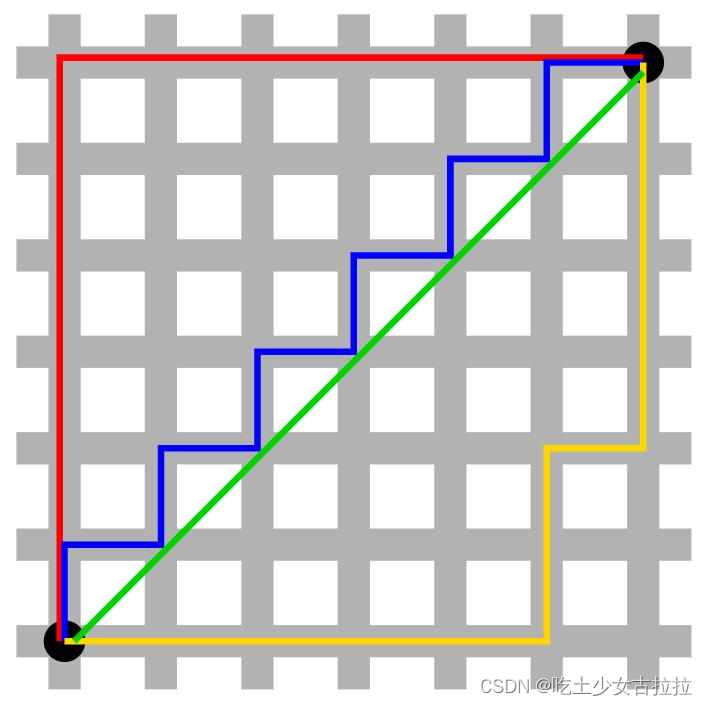
当 P 趋向于正无穷时,即所有向量元素绝对值中的最大值。表示切比雪夫距离。

国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格,因此可以较有效率的到达目的的格子。
-∞-范数
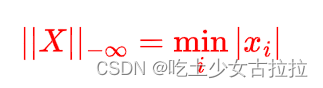
当 P 趋向于负无穷时,即所有向量元素绝对值中的最小值。
5、特殊向量
0 向量
就是分量全部为 0 的向量
[0,0,…,0]
单位向量
就是2-范数为1、模为1、长度为1的向量。
向量 AB 的长度叫做向量的模,记作 ∣ AB ∣。
计算公式:
根据2-范数的公式可知,2-范数就是向量的模,对于向量(列向量)来说,2-范数就是:


![[2021年最新]国产时序性数据TDenige入门](https://img-blog.csdnimg.cn/2021031400022064.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQ0NDkxNzA5,size_16,color_FFFFFF,t_70#pic_center)