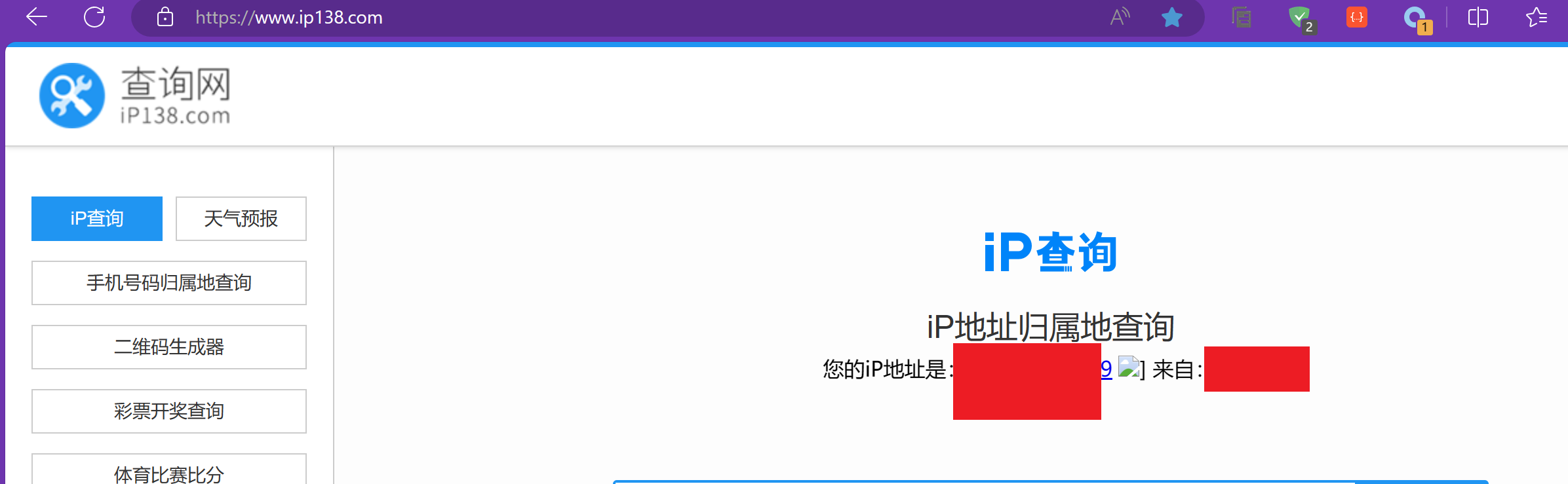
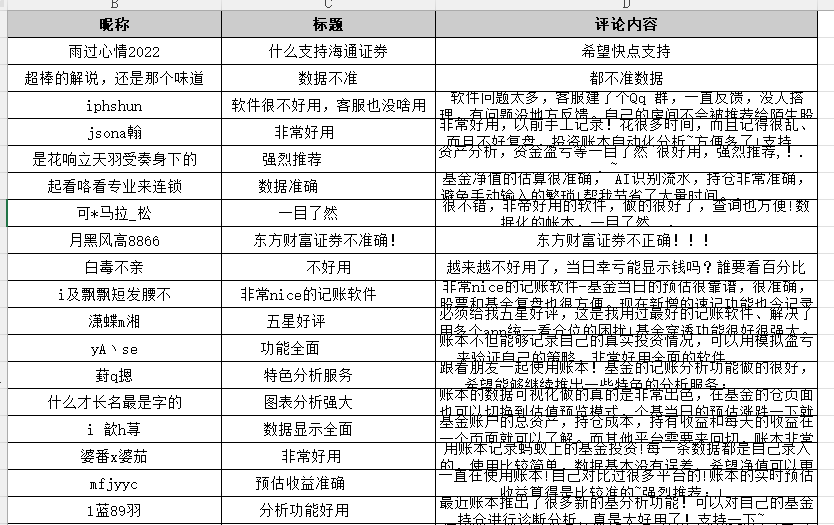
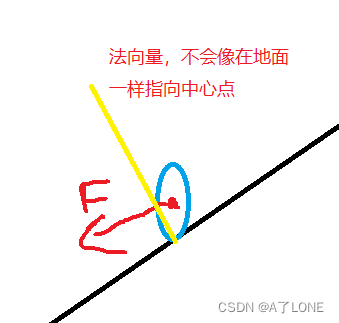
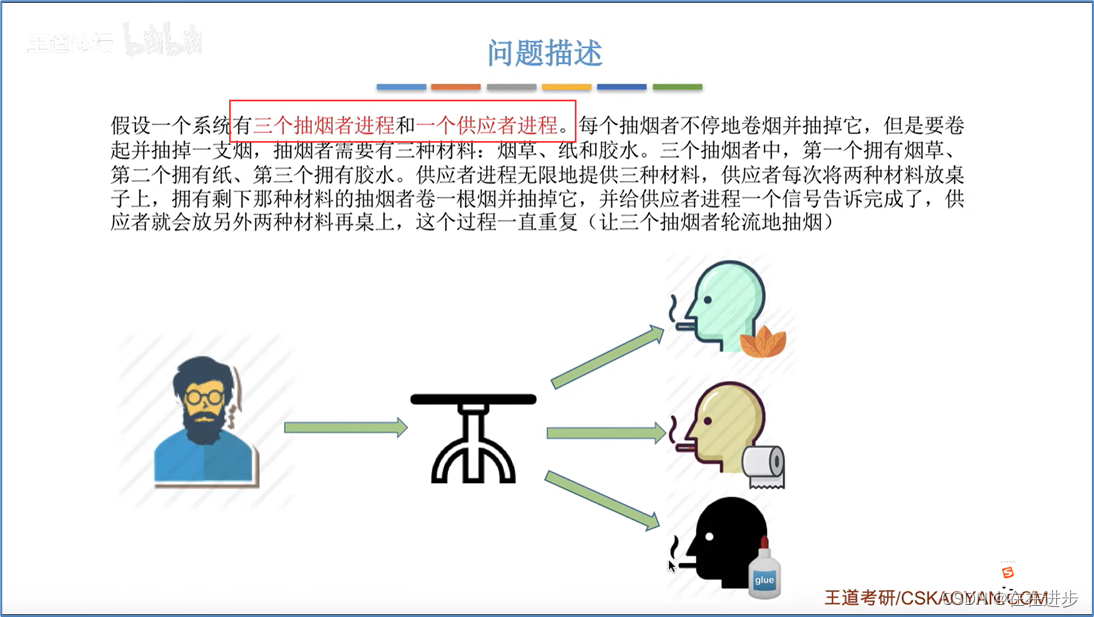
1## 具体思路:
和KMP算法的是想类似,充分利用已经比较字符性质来减少冗余的字符比较次数。KMP的思想是充分的利用模式串中所有前缀字串(以模式串为开头的字串)的真前缀和真后缀(指子串的开始字符与子串的最后字符相等的个数)来减少不必要的字符比较,真前缀和真后缀相等的个数保存在next数组中。扩展KMP算法则是利用子串T中的所有后缀子串suffix[i]与字串T的最长公共前缀来减少字符的比较次数,这个最长公共前缀的个数也记录在next数组中。
假设我们已经求出了extend[0…k]并且记录了a和p,p表示在S串中从第i(i=0…k)个字符开始匹配的过程中达到的最远的位置,a表示取p这个最大值所对应的i值。现在求extend[k+1],可以分下面三种情况:
k+1==p(p肯定是大于或等于k+1的)
直接S[k+1]与T[0]开始比较,并更新a和p的值
k + 1 + next[k - a + 1] <= p
extend[k+1] = next[k - a + 1]
k + 1 + next[k - a + 1] > p
直接S[p]与T[p - k -1]开始比较,extend[k+1]也对应的从p - k - 1开始往后加,并更新a和p的值
对于第二种和第三种情况怎么得到的呢?这就要靠我们保存的a和p了。如果p > k + 1,那么必然有S[k+1,p-1] = T[k-a+1,p-a],这个可以通过S[a,p-1] = T[0,p-a]推出。我们在next[k-a+1]中保存了T的suffix[k-a+1]子串与T的最长公共前缀的长度,假设L=next[k-a+1],那么T[k-a+1,k-a+L]=T[0,L-1]。如果k+1+L<= p,通过S[k+1,p-1] = T[k-a+1,p-a],可以得到S[k+1,k+L]=T[k-a+1,k-a+L]=T[0,L-1],并且S[k+L+1]!=T[0,L]的(因为如果相等的话,T[k-a+1,k-a+L+1]=T[0,L],这与前面的T[k-a+1,k-a+L]=T[0,L-1]是矛盾的),所以extend[k+1]=L。如果k+1+L> p,那么S[k+1,p-1] = T[k-a+1,p-a]=T[0,p-k-2],所以extend[k+1]至少等于p-k-1,然后我们应该继续从p开始比较,因为从p开始都是没有比较过的。
求next的思路和求extend的思路是一样的,只不过是T对自己求extend。
模板:
for(int i = 2; i <= m + n; i ++)
{
if(i <= r) z[i] = min(z[i - l + 1], r - i + 1);
while(s[1 + z[i]] == s[i + z[i]]) z[i] ++;
if(i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
}
例题:

AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int>PII;
const int N=3e5+10;
const int MOD = 1e9 + 7;
const int INF=0X3F3F3F3F;
const int dx[]={-1,1,0,0,-1,-1,+1,+1};
const int dy[]={0,0,-1,1,-1,+1,-1,+1};
const int M = 1e6 + 10;
int z[1001000];
int n, m;
int main()
{
cin >> n;
string a, b;
cin >> a;
cin >> m;
cin >> b;
string s = ' ' + a + b;
int l = 1, r = 0;
z[1] = n + m;//n小m大
for(int i = 2; i <= m + n; i ++)
{
if(i <= r) z[i] = min(z[i - l + 1], r - i + 1);
while(s[1 + z[i]] == s[i + z[i]]) z[i] ++;
if(i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
}
for(int i = n + 1; i <= m + n; i ++)
{
if(z[i] == n) cout << i - n - 1 << " ";
}
return 0;
}