1.赶火车问题。

一列列车从A站开往B站，某人每天赶往B站上车。他已经了解到火车从A站到B站的运行时间是服从均值为30min，标准差为2min的正态随机变量。火车大约下午13：00离开A站，此人大约13:30到达B站。火车离开A站的时刻及概率如表1所示，此人到达B站的时刻及概率如表2所示。问此人能赶上火车的概率有多大？

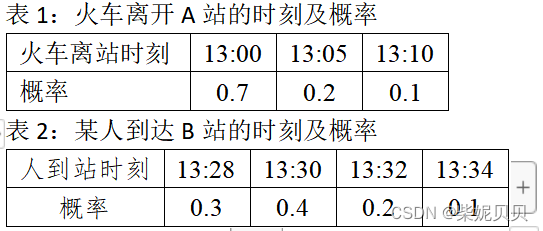
提示：设火车离开的时刻为T1 ，火车运行的时间为T2，该人到达火车站的时间为T3，即为赶上火车。

随机生成正态分布数据
s = np.random.normal(mu, sigma, 1000) # 参数分别为均值、标准差和生成样本数

T2 = np.random.normal(30,2) # 随机生成均值为30，标准差为2的数据

import random

import numpy as np

# 定义火车离开A站时间的均值和标准差
mean_time = 30
std_time = 2

# 定义此人到达B站的时间
arrival_time = 30  # 单位：分钟，大约13:30到达B站

# 定义模拟次数
num_simulations = 10000

# 初始化赶上火车的次数
count = 0

# 进行模拟
for i in range(num_simulations):
    # 生成火车离开A站的随机概率
    prob_A = random.randint(0,1)
    if prob_A <= 0.7:
        T1 = 0
    elif prob_A <= 0.9:
        T1 = 5
    else:
        T1 = 10
    # 生成他到达B站的随机概率
    prob_B = random.randint(0,1)
    if prob_B <= 0.3:
        T3 = 28
    elif prob_B <= 0.7:
        T3 = 30
    else:
        T3 = 34
    # 火车运行的时间T2
    T2 = np.random.normal(30,2) # 随机生成均值为30，标准差为2的数据
    # print(T2)
    # 是否能赶上火车
    if T3 < (T1 + T2):
        count += 1

# 计算赶上火车的概率
probability_caught_train = count / num_simulations
print(f"通过{num_simulations}次模拟，此人能赶上火车的概率是：{probability_caught_train:.2%}")
"""
通过10000次模拟，此人能赶上火车的概率是：71.96%
"""

2.模拟二维随机游动（醉汉回家）

在一个[0,100]×[0,100]的正方形区域内，假设某人的初始位置在点(50,50)处，他周围（前、后、左、右）包括他所站的位置，共有9个格子，每一步随机地移动到一个格子处，也可以保持原地不动。请模拟他的行走路线并作图表示，当他行走到10000步或者出界，则停止模拟。

import numpy as np
import random
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Microsoft YaHei' # 处理文本

# 初始化参数
N = 10000  # 最大步数
bounds = (0, 100)  # 边界
init_position = (50, 50)  # 初始位置

# 创建用于存储位置的数组
positions = np.zeros((N, 2))
positions[0] = init_position

# 定义可能的方向和对应的步长
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]  # 前、后、左、右

# 模拟随机游动
for step in range(1, N):
    # 随机选择一个方向
    direction = random.choice(directions)  # 使用random.choice而不是np.random.choice

    # 计算新位置
    new_position = tuple(np.clip(np.array(positions[step - 1]) + np.array(direction), bounds[0], bounds[1]))

    # 如果新位置在边界内，则更新位置
    if new_position[0] >= bounds[0] and new_position[0] <= bounds[1] and new_position[1] >= bounds[0] and new_position[
        1] <= bounds[1]:
        positions[step] = new_position
    else:
        # 如果新位置出界，则停止模拟
        break

    # 绘制行走路线
plt.figure(figsize=(6, 5))
plt.plot(positions[:, 0], positions[:, 1], marker='*')
plt.xlim(bounds)
plt.ylim(bounds)

plt.xlabel('X 轴')
plt.ylabel('Y 轴')
plt.title('随机游行')
plt.grid(True)
plt.show()

参考赶火车问题