粒子群算法与优化储能策略python实践

粒子群优化算法（Particle Swarm Optimization，简称PSO）, 是1995年J. Kennedy博士和R. C. Eberhart博士一起提出的，它是源于对鸟群捕食行为的研究。粒子群优化算法的基本核心是利用群体中的个体对信息的共享从而使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。

1. 粒子群优化算法的基本原理

在粒子群优化算法中，目标空间中的每个解都可以用一只鸟（粒子）表示，问题中的需求解就是鸟群所要寻找的食物源。在寻找最优解的过程中，每个粒子都存在个体（Personal）行为和群体（Team）行为。每个粒子都会学习同伴的飞行经验和借鉴自己的飞行经验去寻找最优解。每个粒子都会向两个值学习，一个值是个体的历史最优值 $p_{best}$ ；;另一个值是群体的历史最优值（全局最优值） $g_{best}$ 。粒子会根据这两个值来调整自身的速度和位置，而每个位置的优劣都是根据适应度值来确定的。适应度函数是优化的目标函数。

在这里插入图片描述

2. 粒子群优化算法的关键要素

2.1. 适应度

适应度在粒子群优化算法中是一个核心概念，它用于评估解的质量，指导算法搜索的方向。适应度通常由目标函数定义，而目标函数是需要被优化的问题的数学表达。

适应度函数的具体形式取决于优化问题本身，它可以是一个简单的数学函数，也可以是一个复杂的评价模型，取决于问题的复杂性和实际需求。例如，在测试粒子群算法的优化性能时，可能会使用多维多极值的数学函数来进行仿真。

在粒子群算法中，每个粒子都会根据其适应度来更新个体最优位置（pbest）和全局最优位置（gbest）。这些最优位置的发现是算法搜索过程中的关键，它们指导粒子群向潜在的最优解区域移动。粒子通过模仿这两个最优位置来调整自己的速度和位置，从而在解空间中进行高效的搜索。

总的来说，适应度在粒子群优化算法中起到了评价和引导的作用，它帮助算法判断哪些区域更有可能包含最优解，并据此调整搜索策略。

2.2. 速度和位置更新

粒子群优化算法中，粒子的运动是通过维护速度向量和位置向量来描述的。具体来说：

速度向量：速度向量 $v_i$ 描述了粒子在每一维上的移动速度和方向，它决定了粒子下一步迭代中移动的距离和方向。
位置向量：位置向量 $x_i$ 则表示粒子在解空间中的具体位置。

在粒子群优化算法中，每个粒子的速度和位置更新公式可以表示为：

$v_{id}^{k+1} = \omega v_{id}^{k} + c_1 r_1 (p_{id,\text{pbest}}^{k} - x_{id}^{k}) + c_2 r_2 (p_{gd,\text{gbest}}^{k} - x_{id}^{k})$

位置更新公式：
$x_{id}^{k+1} = x_{id}^{k} + v_{id}^{k+1}$

其中：

$v_{id}^{k+1}$ 是粒子 $i$ 在第 $d$ 维上的速度向量的新值。
$x_{id}^{k+1}$ 是粒子 $i$ 在第 $d$ 维上的位置向量的新值。
$\omega$ 是惯性权重，用于控制粒子保持当前速度的能力。
$c_1$ 和 $c_2$ 是学习因子，分别代表个体和社会认知的影响。
$r_1$ 和 $r_2$ 是介于 $[0, 1]$ 之间的随机数。
$p_{id,\text{pbest}}^{k}$ 是粒子 $i$ 在第 $d$ 维上的个人最佳位置。
$p_{gd,\text{gbest}}^{k}$ 是全局最佳位置的第 $d$ 维坐标。
$k$ 表示当前的迭代次数。

从公式的角度来看，PSO算法中的速度更新包含了三个部分：

记忆项： $\omega v_i^k$ ，表示粒子当前速度对下一次速度的影响，有助于保持粒子的运动惯性。
个体认知项： $c_1 \times r_1 \times (p_{id, \text{pbest}}^{k} - x_{id}^{k})$ ，表示粒子向自身历史最佳位置学习的趋势。
社会认知项： $c_2 \times r_2 \times (p_{gd, \text{gbest}}^{k} - x_{id}^{k})$ ，表示粒子向全局最佳位置学习的趋势，体现了粒子间的协同合作和知识共享。

通过这种方式，粒子的速度和位置会根据个体经验和群体经验不断更新，从而使粒子向最优解靠近。粒子群优化算法的这种机制使得它在解决优化问题时具有很强的搜索能力和较快的收敛速度。

2.3. 惯性权重和学习因子

惯性权重（ $ω$ ）控制粒子当前速度对下一次速度的影响程度，有助于保持粒子的运动惯性。学习因子（ $c_1$ ) 和 ( $c_2$ ）则分别影响粒子向个体历史最佳位置和全局最佳位置学习的权重。这些参数的选择对算法的性能有重要影响。

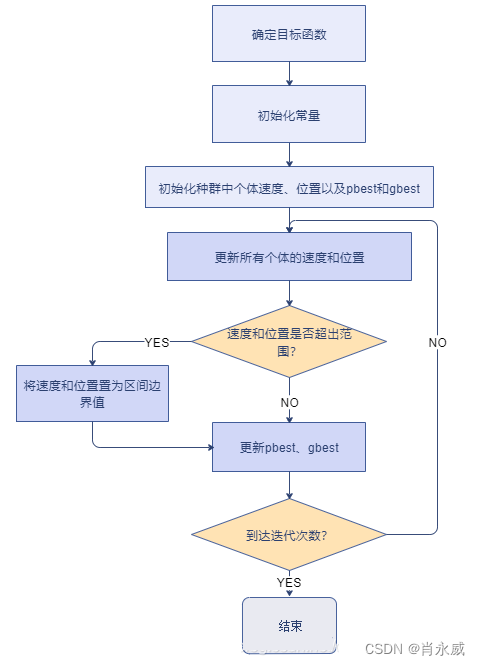
3. 算法流程

确定目标函数。

首先，需要明确优化问题的目标函数，即需要最小化或最大化的函数。目标函数是粒子群优化算法搜索方向的基础，它决定了粒子的适应度如何计算。

初始化：设定粒子群的大小、粒子的初始位置和速度、惯性权重、学习因子等参数。

粒子群大小：确定参与搜索的粒子数量，它影响着搜索的广度和深度。
初始位置和速度：随机生成粒子的初始位置和速度，确保它们在解空间内均匀分布。
惯性权重：设置影响粒子速度保持能力的惯性权重，它影响着算法的收敛速度和搜索能力。
学习因子：设置个体学习因子和社会学习因子，它们决定了粒子向个体历史最佳位置和全局最佳位置学习的权重。

评估适应度：根据适应度函数计算每个粒子的适应度值。

适应度函数用于评估粒子在解空间中的位置优劣，它是算法选择粒子移动方向的基础。根据目标函数计算粒子的适应度值，为后续的更新步骤提供依据。

更新个体历史最佳位置：比较当前粒子的适应度值与个体历史最佳位置的适应度值，如果当前位置更优，则更新个体历史最佳位置。

对于每个粒子，记录其个体历史最佳位置，即适应度值最优的位置。通过比较当前位置和个体历史最佳位置的适应度值，更新个体历史最佳位置。

判断速度和位置是否超出边界范围。

在更新粒子的速度和位置之前，需要检查它们是否超出了预设的边界范围。如果超出边界，需要进行适当的处理，如将速度或位置限制在边界内，或者重新初始化粒子的位置。

更新全局最佳位置：从所有粒子的个体历史最佳位置中选择适应度值最优的位置作为全局最佳位置。

全局最佳位置是整个粒子群在搜索过程中发现的适应度值最优的位置。通过比较所有粒子的个体历史最佳位置的适应度值，选择适应度值最优的位置作为全局最佳位置。

更新速度和位置：根据速度和位置更新公式，计算每个粒子的新速度和位置。

根据速度和位置更新公式，结合个体历史最佳位置和全局最佳位置的信息，计算每个粒子的新速度和位置。这一步骤是粒子群优化算法的核心，通过不断更新粒子的速度和位置，使得粒子群能够向最优解逼近。

迭代：重复步骤3至步骤7，直到达到预设的迭代次数或满足停止条件。

在每次迭代中，重复执行适应度评估、个体历史最佳位置更新、全局最佳位置更新、速度和位置更新的步骤，直到达到预设的迭代次数或者满足其他停止条件（如适应度值达到预设阈值、连续多次迭代适应度值无显著改进等）。最终，算法将输出全局最佳位置作为优化问题的解。

在这里插入图片描述

4. python实践代码

4.1. 算法实现

本文此处源代码来自优秀的博文[1]。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def fit_fun(x):  # 适应函数
    return sum(100.0 * (x[0][1:] - x[0][:-1] ** 2.0) ** 2.0 + (1 - x[0][:-1]) ** 2.0)

class Particle:
    # 初始化
    def __init__(self, x_max, max_vel, dim):
        self.__pos = np.random.uniform(-x_max, x_max, (1, dim))  # 粒子的位置
        self.__vel = np.random.uniform(-max_vel, max_vel, (1, dim))  # 粒子的速度
        self.__bestPos = np.zeros((1, dim))  # 粒子最好的位置
        self.__fitnessValue = fit_fun(self.__pos)  # 适应度函数值

    def set_pos(self, value):
        self.__pos = value

    def get_pos(self):
        return self.__pos

    def set_best_pos(self, value):
        self.__bestPos = value

    def get_best_pos(self):
        return self.__bestPos

    def set_vel(self, value):
        self.__vel = value

    def get_vel(self):
        return self.__vel

    def set_fitness_value(self, value):
        self.__fitnessValue = value

    def get_fitness_value(self):
        return self.__fitnessValue

class PSO:
    def __init__(self, dim, size, iter_num, x_max, max_vel, tol, best_fitness_value=float('Inf'), C1=2, C2=2, W=1):
        self.C1 = C1
        self.C2 = C2
        self.W = W
        self.dim = dim  # 粒子的维度
        self.size = size  # 粒子个数
        self.iter_num = iter_num  # 迭代次数
        self.x_max = x_max
        self.max_vel = max_vel  # 粒子最大速度
        self.tol = tol  # 截至条件
        self.best_fitness_value = best_fitness_value
        self.best_position = np.zeros((1, dim))  # 种群最优位置
        self.fitness_val_list = []  # 每次迭代最优适应值

        # 对种群进行初始化
        self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]

    def set_bestFitnessValue(self, value):
        self.best_fitness_value = value

    def get_bestFitnessValue(self):
        return self.best_fitness_value

    def set_bestPosition(self, value):
        self.best_position = value

    def get_bestPosition(self):
        return self.best_position

    # 更新速度
    def update_vel(self, part):
        vel_value = self.W * part.get_vel() + self.C1 * np.random.rand() * (part.get_best_pos() - part.get_pos()) \
                    + self.C2 * np.random.rand() * (self.get_bestPosition() - part.get_pos())
        vel_value[vel_value > self.max_vel] = self.max_vel
        vel_value[vel_value < -self.max_vel] = -self.max_vel
        part.set_vel(vel_value)

    # 更新位置
    def update_pos(self, part):
        pos_value = part.get_pos() + part.get_vel()
        part.set_pos(pos_value)
        value = fit_fun(part.get_pos())
        if value < part.get_fitness_value():
            part.set_fitness_value(value)
            part.set_best_pos(pos_value)
        if value < self.get_bestFitnessValue():
            self.set_bestFitnessValue(value)
            self.set_bestPosition(pos_value)

    def update_ndim(self):

        for i in range(self.iter_num):
            for part in self.Particle_list:
                self.update_vel(part)  # 更新速度
                self.update_pos(part)  # 更新位置
            self.fitness_val_list.append(self.get_bestFitnessValue())  # 每次迭代完把当前的最优适应度存到列表
            print('第{}次最佳适应值为{}'.format(i, self.get_bestFitnessValue()))
            if self.get_bestFitnessValue() < self.tol:
                break

        return self.fitness_val_list, self.get_bestPosition()

if __name__ == '__main__':
    pso = PSO(4, 5, 10000, 30, 60, 1e-4, C1=2, C2=2, W=1)
    fit_var_list, best_pos = pso.update_ndim()
    print("最优位置:" + str(best_pos))
    print("最优解:" + str(fit_var_list[-1]))
    plt.plot(range(len(fit_var_list)), fit_var_list, alpha=0.5)

4.2. 算法应用

用粒子群算法实现储能配置优化，已知24小时负荷曲线、24小时峰谷平电价，采用峰谷套利商业模式，以经济最优为目标函数，寻找最优的储能容量，求解储能容量，输出收益和储能容量。

目标函数：

$\text{Maximize} \quad profit = \sum_{t=0}^{24} p_{t, \text discharge} price_t - \sum_{t=0}^{24} p_{t, \text charge} (price_t+pprice) - \sum_{t=0}^{24} \eta C_{max}price_t$

其中，充电与放电相等， $\sum_{t=0}^{24} p_{t, \text charge} =\sum_{t=0}^{24} p_{t, \text discharge}$ ， $price_t$ 对应price24中的数据。
$\eta$ 是变压器系统效率

约束条件包括：

每个时段的负荷需求必须得到满足。
储能充放电有先后顺序，最开始能量是0，从0开始充电，最后放到0。
储能容量定义为 $C_{max}= \max(C_t)$ 。
储能最大充电功率是 $P_{\text{max charge}}=0.5C_{max}$ ，储能最大放电功率是 $P_{\text{max discharge}}=0.5C_{max}$ 。
负荷需求平衡： $P_t^{\text{from grid}} + P_t^{\text{discharge}} = P_t^{\text{load}} + P_t^{\text{charge}}$ ，其中，4个变量分别是电网供电功率、储能放电功率、负荷功率、储能充电功率。其中， $P_t^{\text{load}}$ 对应load24中的数据。
充放电功率限制： $\leq P_t^{\text{charge}} \leq P_{\text{max charge}}$ ， $\leq P_t^{\text{discharge}} \leq P_{\text{max discharge}}$
当前储能能量： $C_t =C_{t-1} + P_t^{\text{charge}} + P_t^{\text{discharge}}$
负载小于变压器容量： $p_{t, \text charge} + p_{t, \text discharge} <C_{max}$

粒子群算法中的每个粒子将代表一种可能的24小时充放电策略，而适应度（fitness）将由这个目标函数计算得出。粒子24个维度，位置代表着储能充放电功率（或电量），正数为充电，负数为放电，粒子速度代表充放电变化率，便于算法调优。

详见参考代码。

import numpy as np

class Particle:
    def __init__(self, dim, max_charge):
        #self.__charge = np.random.uniform(-max_charge, max_charge, dim)  # 粒子的充放电策略
        half_dim = dim // 2
        charge_positive = np.random.uniform(0, max_charge, half_dim)
        charge_negative = -charge_positive
        charge_last = np.concatenate((charge_positive[1:], charge_negative))
        np.random.shuffle(charge_last)  # 打乱顺序，使得充电和放电时段随机分布
        self.__charge = np.concatenate((charge_positive[0:1], charge_last))
        
        
        self.__transformer_capacity = np.random.uniform(2500, 3000)  # 变压器容量
        self.__velocity = np.random.uniform(0, 100, dim)  # 粒子的速度，初始设为0
        self.__fitness_value = float('-inf')  # 适应度函数值

    def set_charge(self, value):
        self.__charge = value

    def get_charge(self):
        return self.__charge

    def set_velocity(self, value):
        self.__velocity = value

    def get_velocity(self):
        return self.__velocity

    def set_transformer_capacity(self, value):
        self.__transformer_capacity = value

    def get_transformer_capacity(self):
        return self.__transformer_capacity

    def set_fitness_value(self, value):
        self.__fitness_value = value

    def get_fitness_value(self):
        return self.__fitness_value


class PSO:
    def __init__(self, dim, size, iter_num, max_charge, load, price, pprice, efficiency, loss, penalty_factor=0.1, C1=2, C2=2, W=1):
        self.C1 = C1
        self.C2 = C2
        self.W = W
        self.dim = dim  # 粒子的维度，即时间段数量
        self.size = size  # 粒子个数
        self.iter_num = iter_num  # 迭代次数
        self.max_charge = max_charge # 储能最大充电功率
        self.load = load  # 负荷需求数据
        self.price = price  # 电价数据
        self.pprice = pprice  # 平准度电成本
        self.efficiency = efficiency  # 系统效率
        self.loss = loss  # 变压器损耗
        self.penalty_factor = penalty_factor  # 惩罚系数
        self.best_fitness_value = float('-inf')  # 种群最优适应度
        self.best_position = np.zeros(dim)  # 种群最优位置
        self.fitness_val_list = []  # 每次迭代最优适应值
        self.energy_cap = 2*max_charge  # 储能容量
        self.transformer_cap = max(load) # 变压器容量

        # 对种群进行初始化
        self.particles = [Particle(dim, max_charge) for _ in range(size)]

    # 计算适应度函数值
    def calculate_fitness(self, particle):
        charge = particle.get_charge()  # 粒子的充电策略
        transformer_capacity = particle.get_transformer_capacity()  # 变压器容量

        # 负载超负荷惩罚
        violation_penalty = 0

        # 负荷需求平衡约束和收益计算
        total_profit = 0
        energy = 0
        for t in range(self.dim):
            # 负载超负荷惩罚
            if charge[t] + self.load[t] >= transformer_capacity:
                violation_penalty += 10 # 计算违反约束的惩罚，可以根据实际情况调整惩罚系数 
            elif charge[t] + self.load[t] < 0:  
                violation_penalty += 20 # 计算违反约束的惩罚，可以根据实际情况调整惩罚系数         
            
            if t > 0:
                energy += charge[t-1] * self.efficiency  # 计算当前时刻的储能能量，考虑系统效率

            if energy < -1:
                violation_penalty += 10 + abs(energy)  # 计算违反约束的惩罚，需要满足负载需求

            # 计算当前时刻的收益
            if charge[t] >= 0:  # 充电
                profit_t = - charge[t] * (self.price[t] + self.pprice)

            else:               # 放电
                profit_t = - charge[t] * self.price[t]
                    
            total_profit += profit_t - transformer_capacity * self.loss

        if abs(energy) <= 1:
            violation_penalty += 1  # 违反充放电平衡的惩罚，可以根据实际情况调整惩罚系数

        # 应用惩罚项
        fitness = (total_profit - violation_penalty * self.penalty_factor)  # 使用惩罚系数对适应度进行惩罚
        
        print(total_profit, fitness)

        return fitness

    # 修改储能参数
    def update_energy_param(self, particle):
        charge = particle.get_charge()  # 粒子的充电策略

        energy = 0
        energy_list = []
        for t in range(self.dim):  
            if t > 0:
                energy += charge[t-1] * self.efficiency  # 计算当前时刻的储能能量，考虑系统效率
                energy_list.append(energy)
        # 取最大数为储能容量          
        self.Cap_max = max(energy_list)
        self.max_charge = 0.5*self.Cap_max
        self.max_discharge = -0.5*self.Cap_max   


    # 更新最优位置和最优适应度
    def update_best_position(self, particle):
        fitness_value = self.calculate_fitness(particle)
        if fitness_value > particle.get_fitness_value():
            particle.set_fitness_value(fitness_value)
            particle_charge = particle.get_charge()
            particle.set_best_charge(particle.get_charge())
            self.best_fitness_value = fitness_value
            self.best_position = particle_charge

    # 更新速度和位置
    def update_particle(self, particle):
        velocity = self.W * particle.get_velocity() + \
                    self.C1 * np.random.rand() * (particle.get_charge() - particle.get_charge()) + \
                    self.C2 * np.random.rand() * (self.best_position - particle.get_charge())
        # 边界检查
        charge = particle.get_charge()
    
        # 更新速度
        new_velocity = charge - velocity
        new_velocity[new_velocity > self.max_charge] = self.max_charge  # 速度上限
        new_velocity[new_velocity < -self.max_charge] = -self.max_charge  # 速度下限
        particle.set_velocity(new_velocity)    
        
        # 更新位置
        new_charge = charge + new_velocity
        new_charge[new_charge > self.max_charge] = self.max_charge  # 充电上限
        new_charge[new_charge < -self.max_charge] = -self.max_charge  # 放电下限
        particle.set_charge(new_charge)


    # 更新全局最优位置和适应度值
    def update_global_best(self):
        for particle in self.particles:
            self.update_best_position(particle)

    # 粒子群优化算法
    def optimize(self):
        for _ in range(self.iter_num):
            self.update_global_best()
            self.fitness_val_list.append(self.best_fitness_value)
            for particle in self.particles:
                self.update_particle(particle)
        return self.best_position, self.best_fitness_value, self.fitness_val_list

if __name__ == '__main__':
    load24 = np.array([1336.8, 821.8, 594.5, 575.4, 546.9, 745, 933.1, 514.1, 140, 67.1, 61, 118.7, 1241.8, 1102, 1009.8, 1239.7, 826, 136.4, 76.1, 112.3, 103.4, 81.4, 355.5, 1859.6])
    price24 = np.array([0.32, 0.32, 0.32, 0.32, 0.32, 0.32, 0.32, 0.32, 0.69, 1.13, 1.13, 1.13, 0.69, 0.69, 0.69, 0.69, 0.69, 1.13, 1.13, 1.13, 1.13, 1.13, 0.69, 0.32])
    pprice = 0.44
    efficiency = 1.0  # 系统效率
    loss = 0.01  # 变压器损耗
    penalty_factor = 0.1  # 惩罚系数

    pso = PSO(dim=24, size=10, iter_num=30000, max_charge=500, load=load24, price=price24, pprice=pprice,
              efficiency=efficiency, loss=loss, penalty_factor=penalty_factor, C1=2, C2=2, W=0.5)
    best_position, best_profit, fitness_val_list = pso.optimize()

    print("最优充电策略:", best_position)
    print("最优收益:", best_profit)

10万次迭代输出结果：
在这里插入图片描述

注；在充放电顺序24个时序过程中，这些粒子位置是一维数据，在逐个累加过程中，需要确保累加电量始终大于0，到最后放完电归零，其中，首个是充电大于零。

输出结果很不理想，欢迎讨论如何设计更合理。

5. 总结

粒子群优化算法通过模拟鸟群捕食行为中的信息共享和协作机制，实现了在解空间中从无序到有序的搜索过程。通过不断更新粒子的速度和位置，算法能够逐渐逼近问题的最优解。在实际应用中，粒子群优化算法已广泛应用于各种优化问题，如函数优化、机器学习参数调整等。通过合理设置算法参数和适应度函数，可以进一步提高算法的搜索效率和求解质量。

参考：

[1]. 爱学习的贝塔. 粒子群算法python（含例程代码与详解). CSDN博客. 2020.10

[2]. zadarmo_. 第二次培训之粒子群算法. CSDN博客. 2020.07