来源：https://www.bilibili.com/video/BV16A411T7zX/?spm_id_from=333.337.search-card.all.click&vd_source=7a1a0bc74158c6993c7355c5490fc600

---

奇异值分解其实就是如下图，把矩阵 M 分解成一个正交方阵 U，乘以一个不规则奇异值矩阵 sigma，再乘以一个正交方阵 V^T

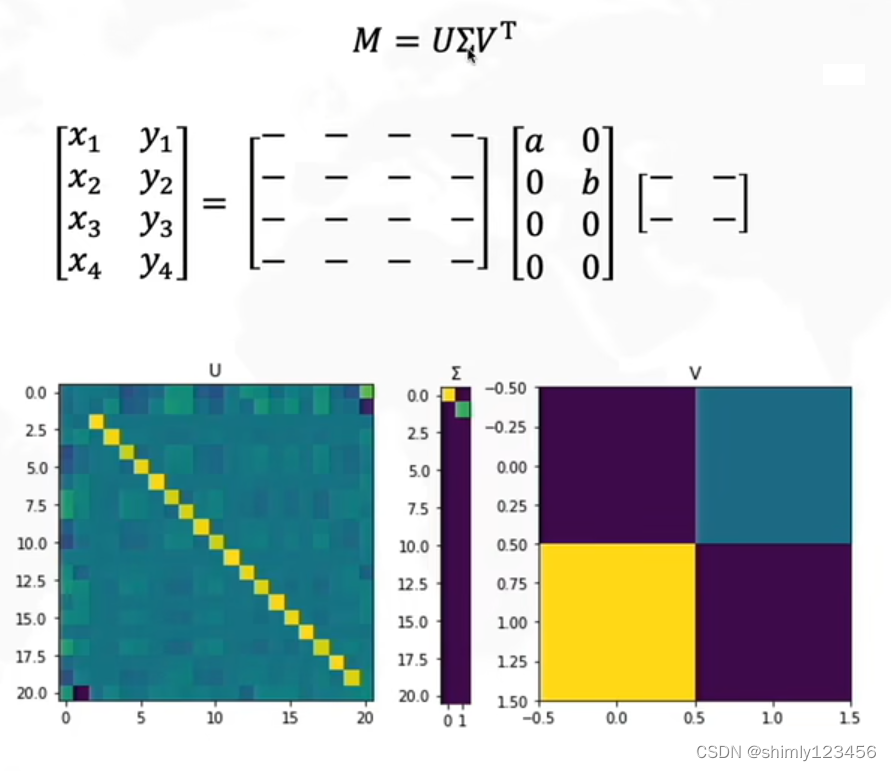
先复习一下线性变换，如下图，S矩阵是一个拉伸矩阵

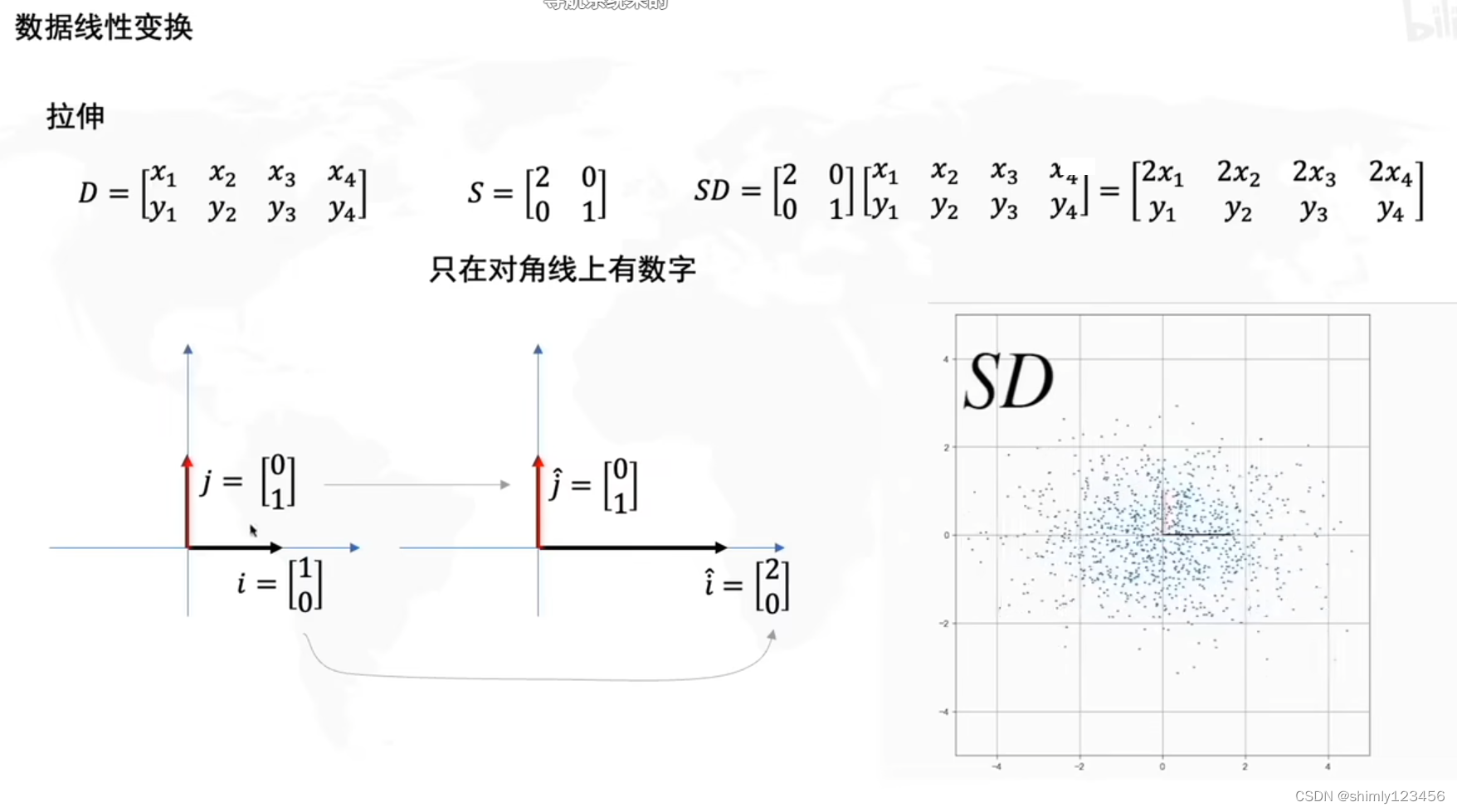
如下，R矩阵是旋转矩阵，RSD 就是先拉伸再旋转

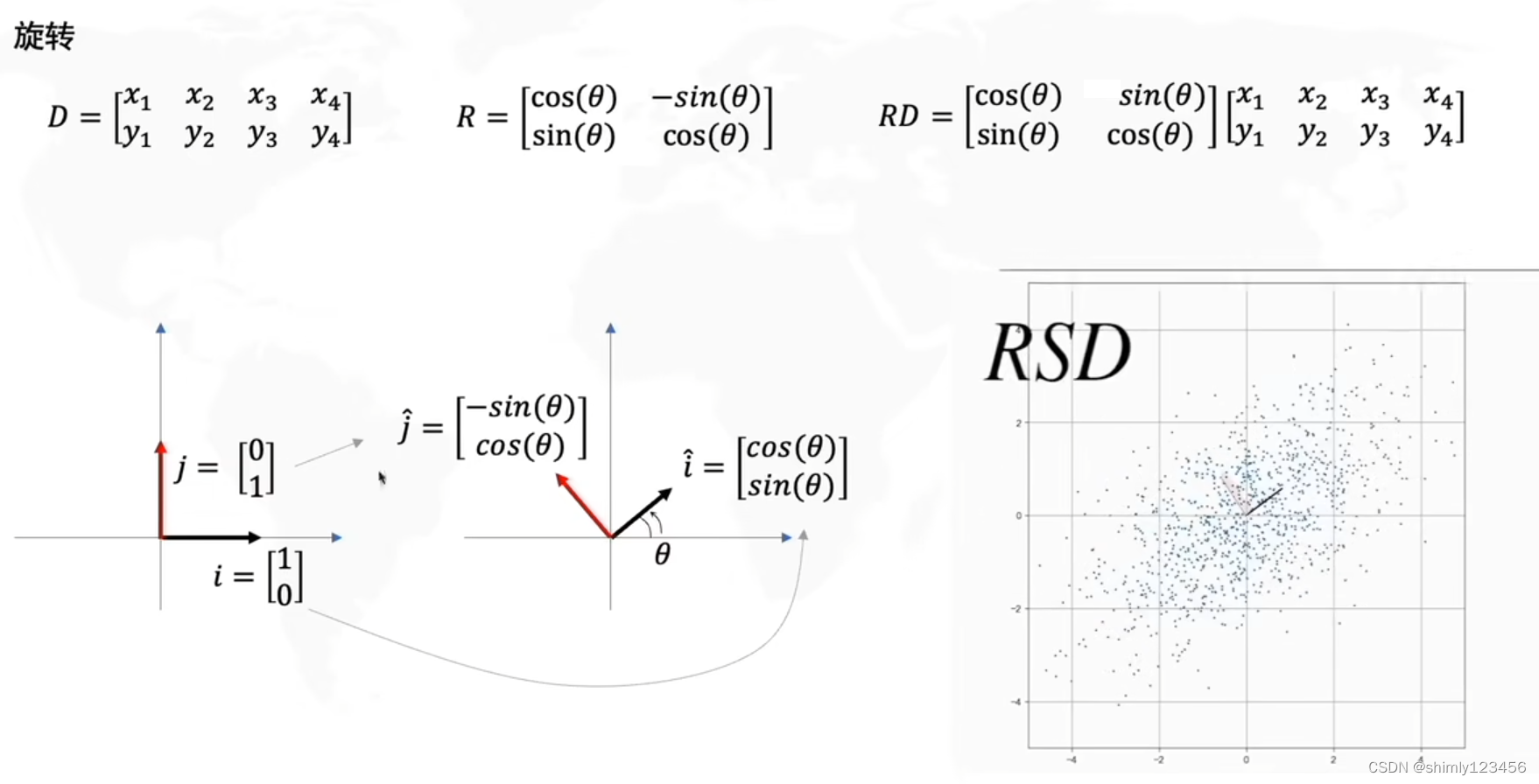
在 2x2 的矩阵上的 SVD 可以把 M 分解为 两个旋转矩阵和一个拉伸矩阵 （先旋转再拉伸再旋转）

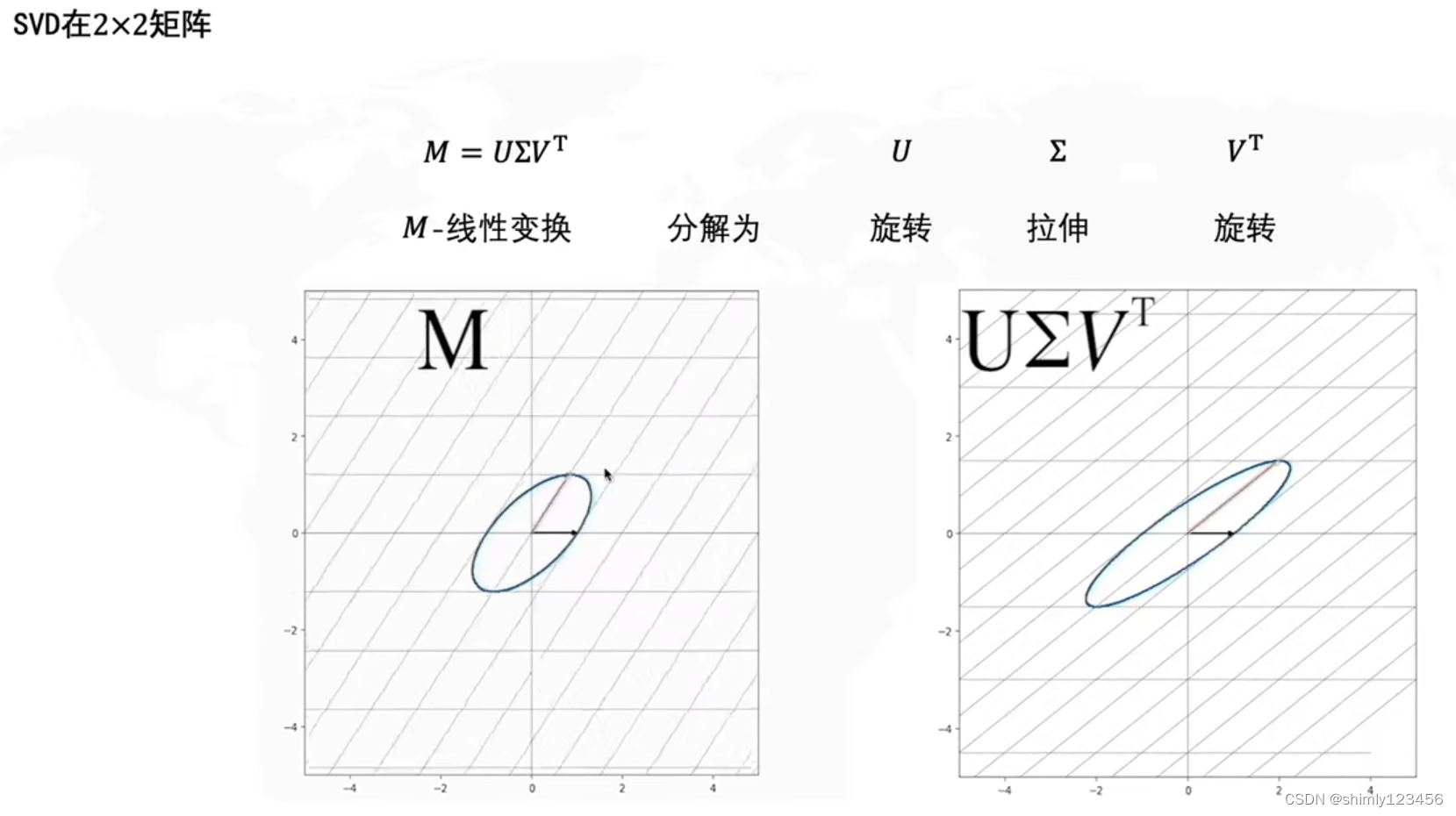
2x2矩阵中的 SVD 可以定义成：原始域标准正交基 V 经过 M 线性变换后，得到 U sigma

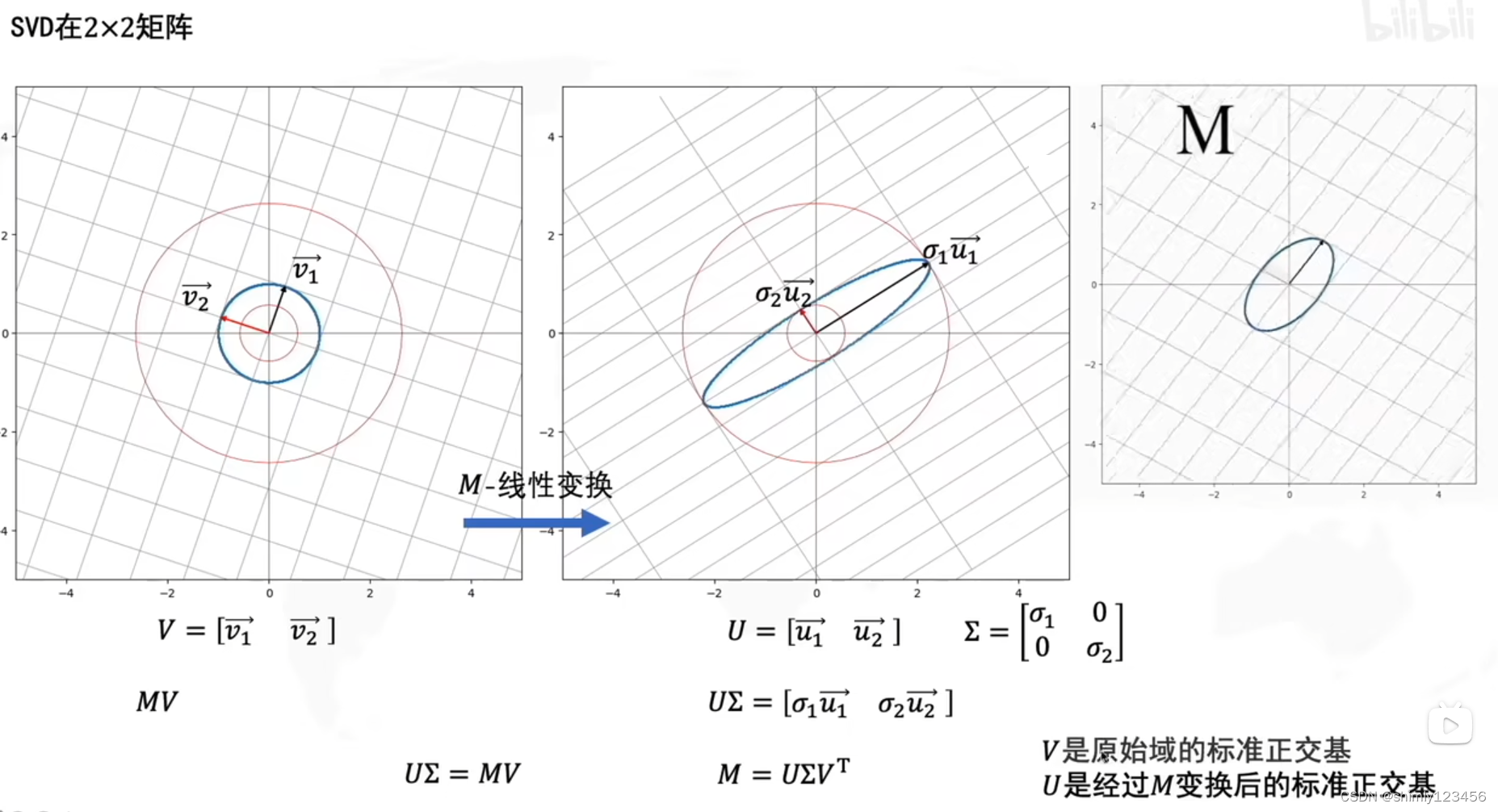
如下，是推广到任意大小矩阵的 SVD

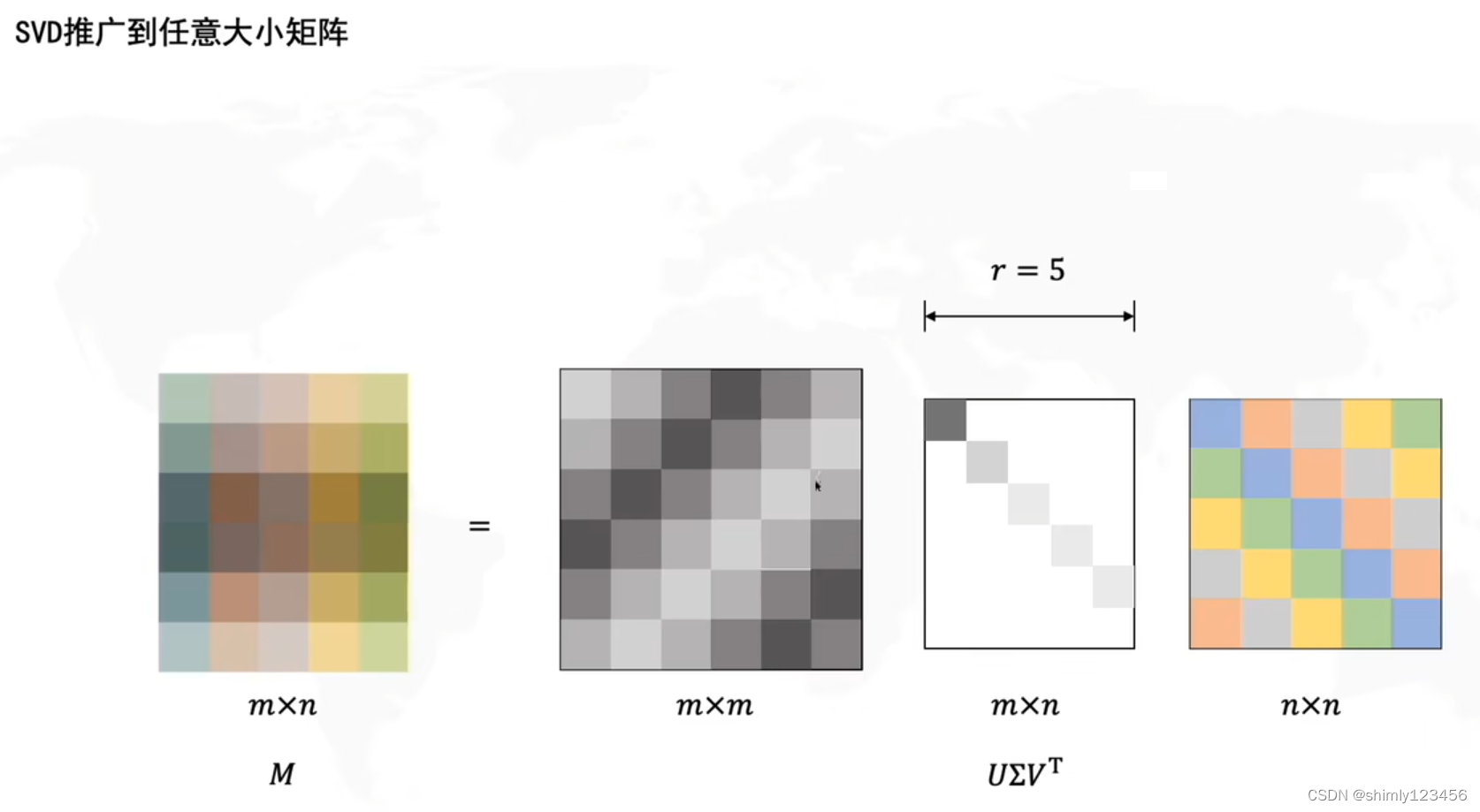
由于 sigma 矩阵的最后一行全是 0，没有意义；同时，U 矩阵的最后一列总是和 sigma 矩阵的最后一行相乘，也没有意义，所以我们可以去掉 U 矩阵的最后一列和 sigma 矩阵的最后一行，如下图

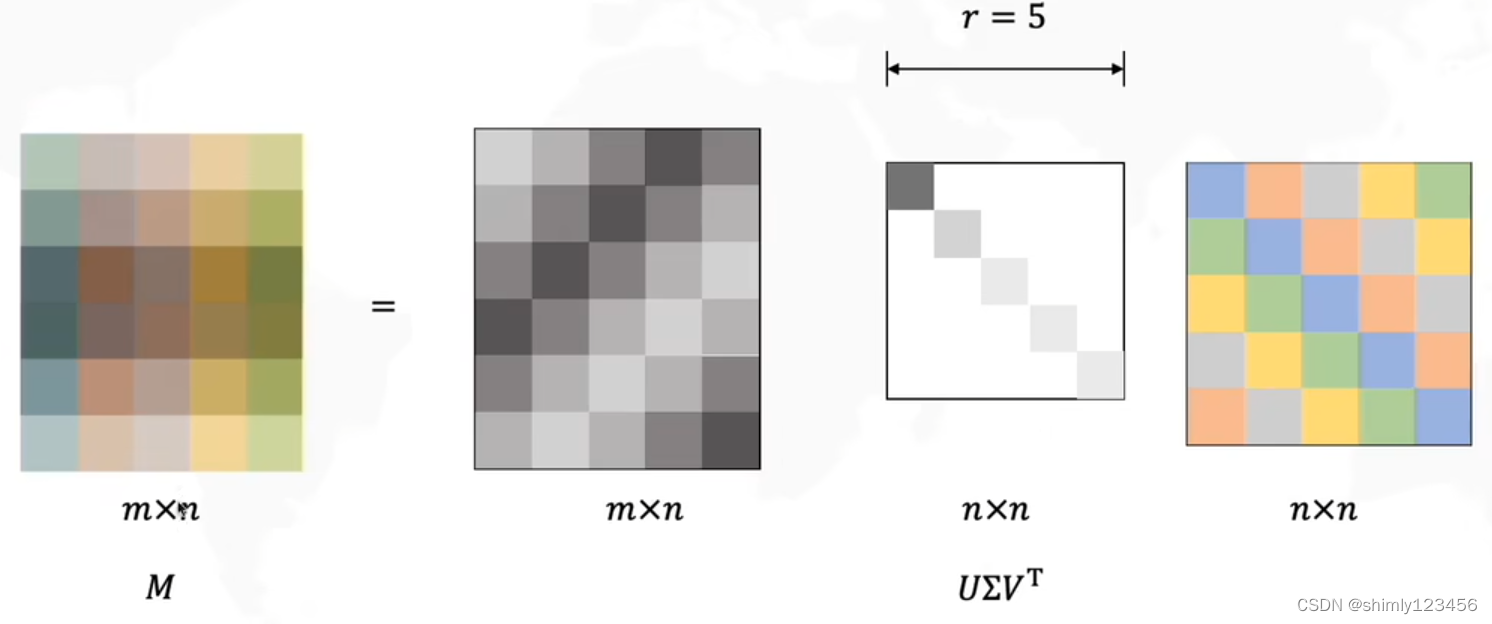
需要注意的是：sigma 矩阵的奇异值从上到下是从大到小排列的，每一个奇异值代表一个正交基。越是重要的正交基(轴方向)的奇异值越大，所以，sigma 矩阵从上到小的奇异值重要性是降低的。因此，我们可以去掉最下面的奇异值，来去掉没那么重要的正交基，从而降维、压缩，这也就叫做 TruncatedSVD 截断奇异值分解

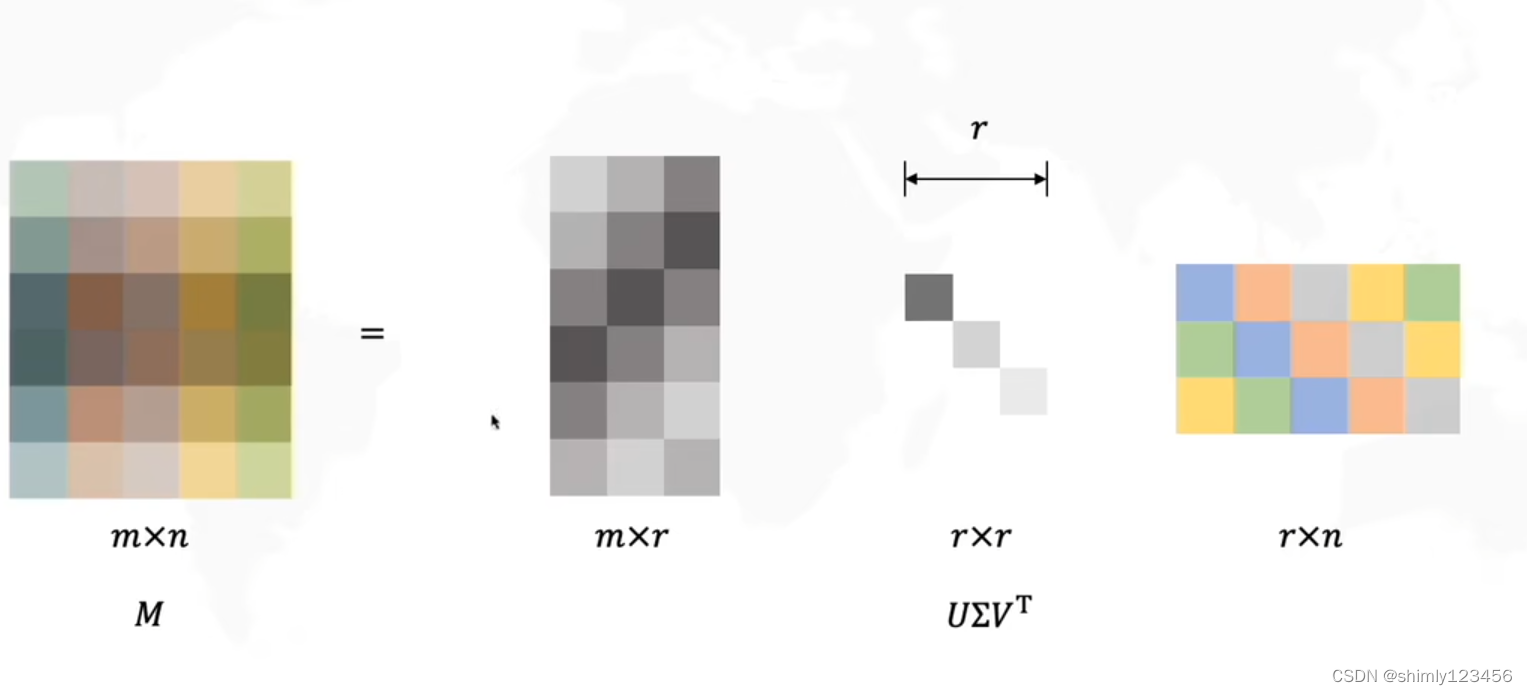
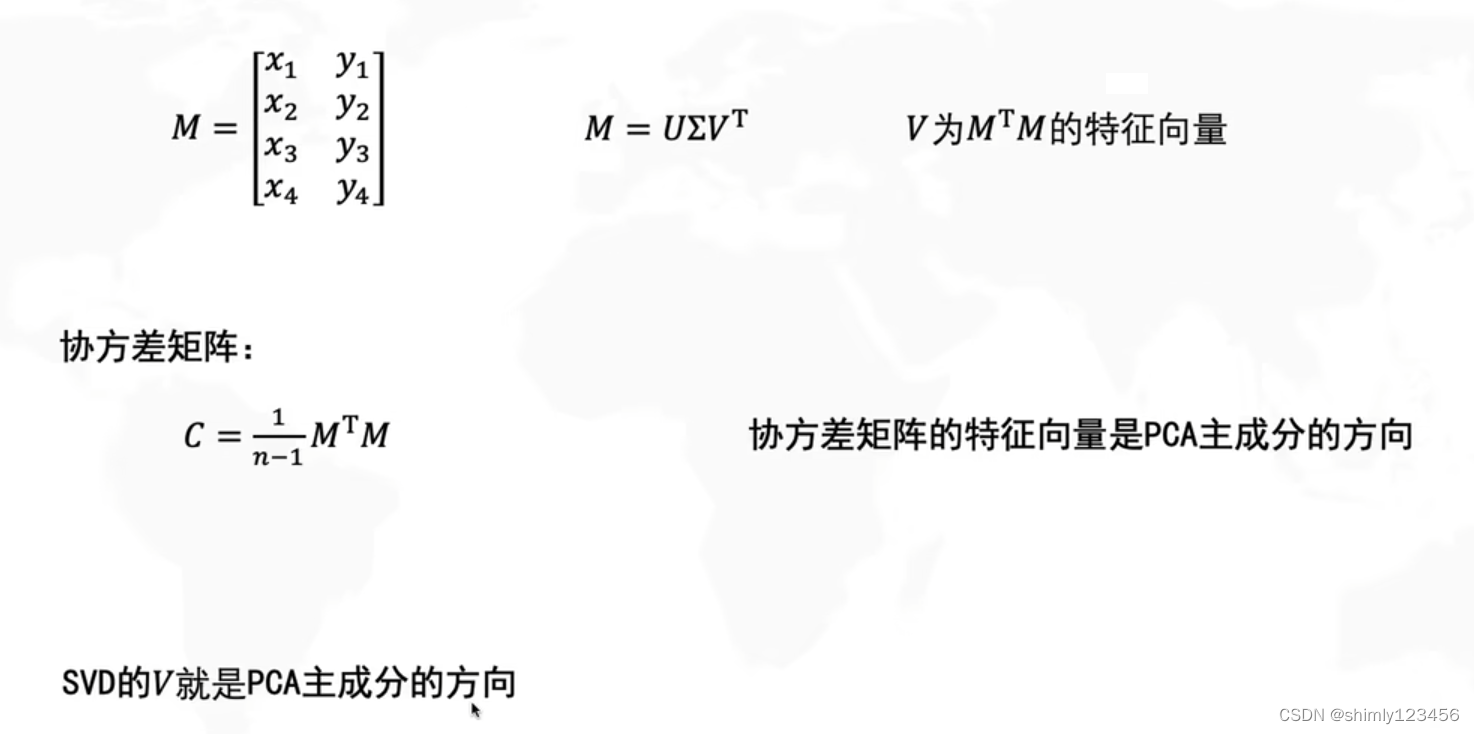
如下图，计算 V 的方法是求 M^TM 的特征向量，计算 U 的方法是求 MM^T 的特征向量，求 sigma 是对它们的特征值开方

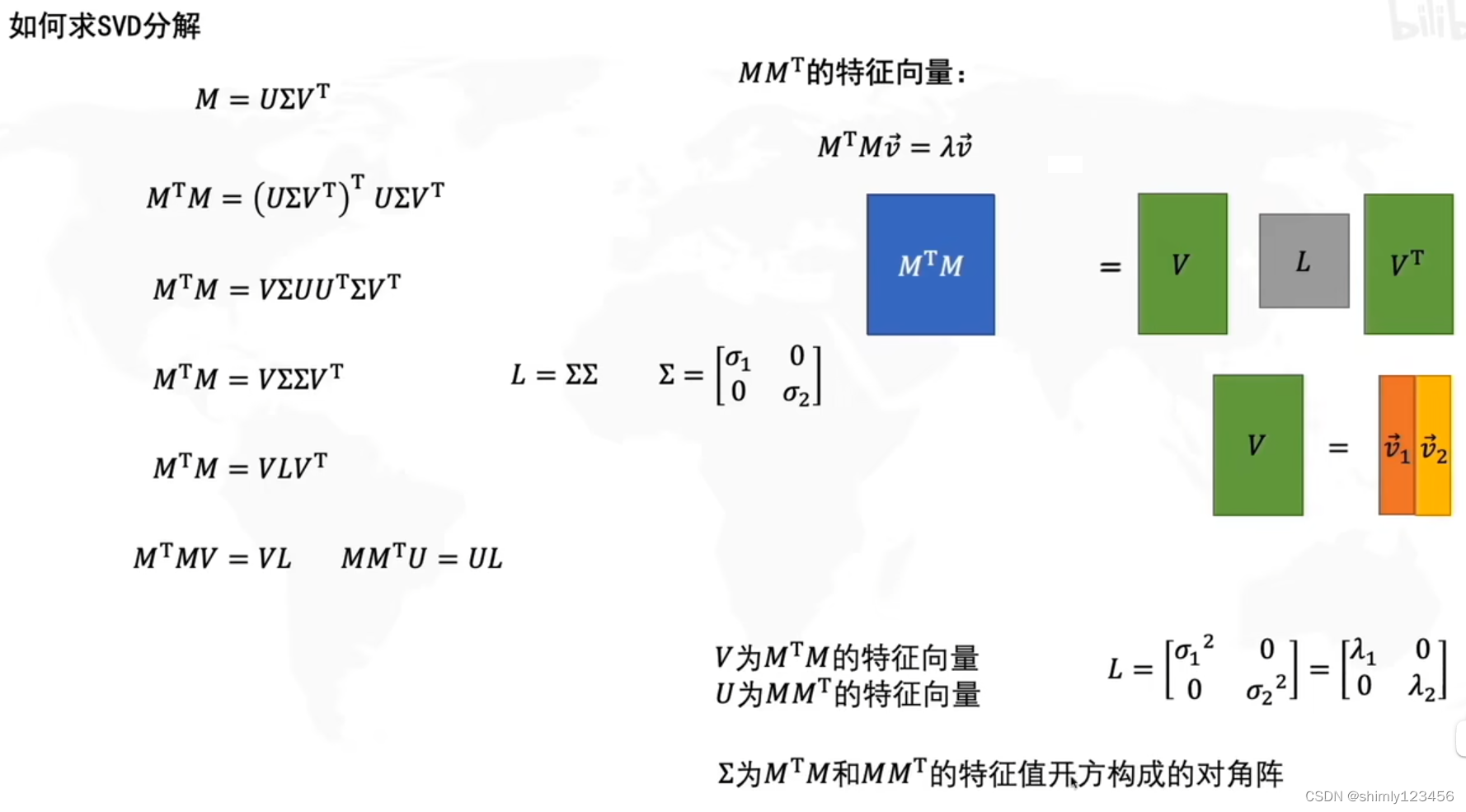
协方差矩阵的特征向量就是 PCA 主成分的方向，换句话说，SVD 的 V 就是 PCA 主成分的方向

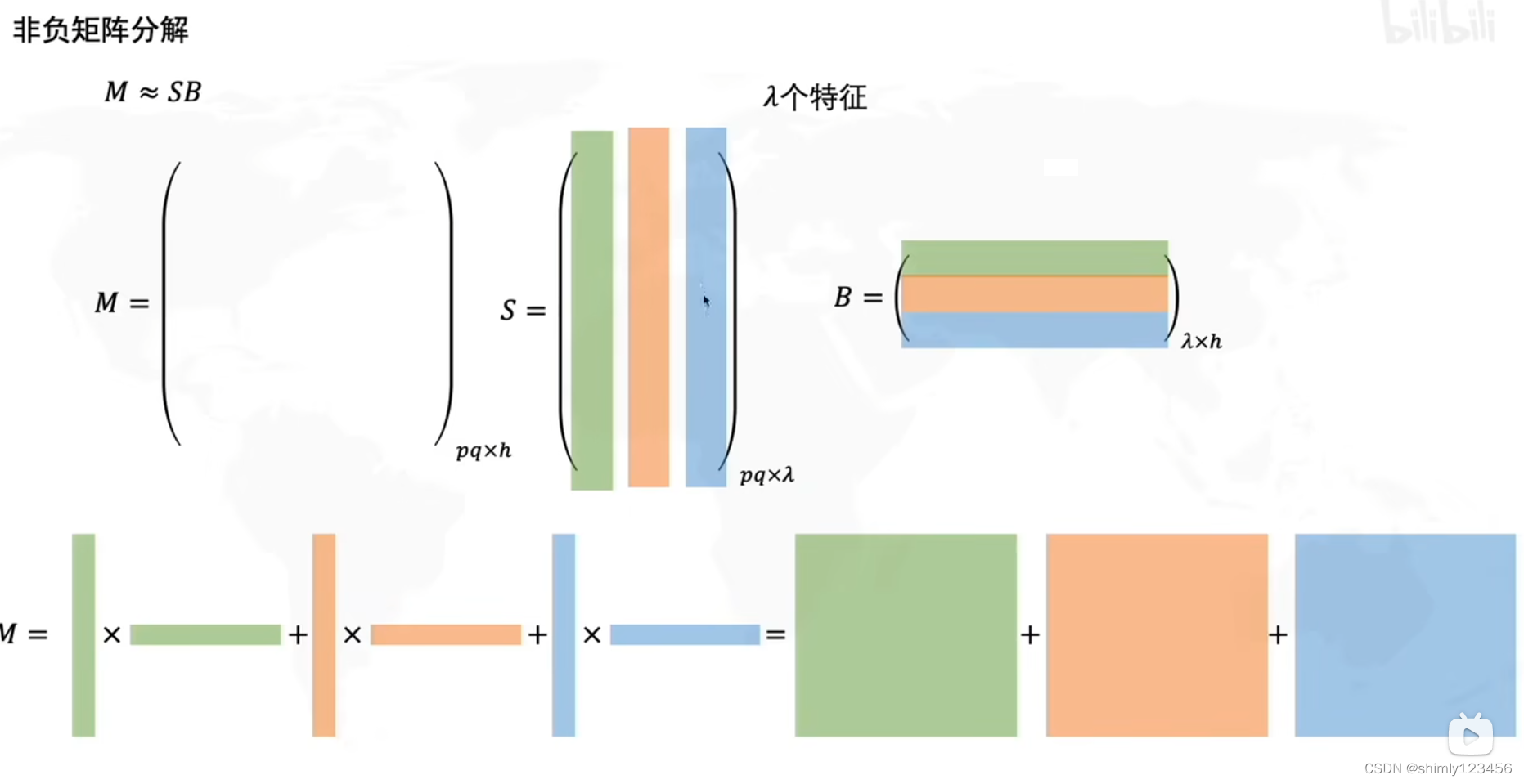
非负矩阵分解的 S 和 B 两个矩阵都要求必须是正数，它跟 SVD 很相似。但在需要解释矩阵的物理意义时会更加容易