【六十】【算法分析与设计】用一道题目解决dfs深度优先遍历，dfs中节点信息，dfs递归函数模板进入前维护出去前回溯，唯一解的剪枝飞升返回值true

news2024/11/15 9:39:55

路径之谜

题目描述

小明冒充X星球的骑士,进入了一个奇怪的城堡。

城堡里边什么都没有,只有方形石头铺成的地面。

假设城堡地面是n×n个方格。如下图所示。

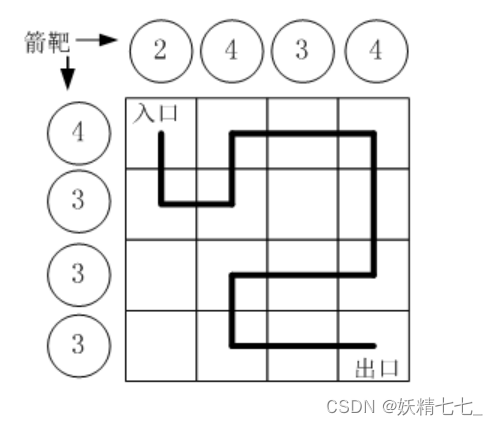
1e8908abd7eb470083d000bb49a7bab3.png

按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着音走,也不能跳跃。每走到一个新方格,就要向正北

方和正西方各射一箭。(城堡的西墙和北墙内各有12个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只

给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比比如上图中的例子。

本题的要求就是已知箭靶数字,求骑士的行走路径(测试)数据保证路径唯一)

输入描述

第一行一个整数N(0<N<20),表示地面有NXN个方格。

第二行N个整数,空格分开,表示北边的箭靶上的数字(自西向东)

第三行N个整数,空格分开,表示西边的箭靶上的数字(自北向南)

输出描述

输出一行若干个整数,表示骑士路径。

为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号号:0,1,2,3

比如,上图中的方块编号为:

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15

输入输出样例

示例

输入

4

2 4 3 4

4 3 3 3

输出

0 4 5 1 2 3 7 11 10 9 13 14 15

运行限制

最大运行时间:5s

最大运行内存:256M

12c651f1c7234b9988867f9e74ddcf2e.png

暴力递归

1.

定义dfs(i,j)表示当前节点坐标。

假设入口位置坐标是（1，1），往下是row行，往右是col列。

定义row记录从入口到当前节点这条路径西边靶子的数量，row[1]表示西边第一个靶子上箭的数量，row[2]表示西边第二个靶子上箭的数量...以此类推。

定义col记录从入口到当前节点这条路径北边靶子的数量，col[1]表示北边第一个靶子上箭的数量，col[2]表示北边第二个靶子上箭的数量...以此类推。

定义path记录从入口到当前节点的路径信息。

定义visit记录从入口到当前节点，这条路径，当前所有位置访问情况，访问过为true，没有被访问过false。

2.

也就是当前节点的信息不止有(i,j)还有path，row，col，visit四个变量共同组成。

3.

dfs内部逻辑，进入当前节点的时候，维护当前节点的所有信息。

离开当前节点返回之前，回溯，消除当前节点维护的所有信息。

4.

夹在中间的就是计算逻辑，写代码的时候先把首位维护和回溯写掉，然后在中间加主要逻辑。

 
void dfs(int i, int j) {
    visit[i][j] = true;
    row[i]++;
    col[j]++;
    path.push_back((i - 1) * n + (j - 1));//数学推导不细说，找规律
    //添加主要逻辑
    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
}

 

5.

06e70e01efad4a72a6044d401aaf9bae.png

对于当前节点，下一个遍历的节点位置有四个，上下左右，但是有一些位置需要剪枝。

规则是，第一，这四个位置首先不能越界，第二，这四个位置不能被访问过，被访问过表示已经是路径上的点，已经走过了。如果满足要求就可以dfs进入下一节点。

 
void dfs(int i, int j) {
    visit[i][j] = true;
    row[i]++;
    col[j]++;
    path.push_back((i - 1) * n + (j - 1));

    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
            dfs(x, y);
        }
    }

    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
}

 

6.

思考递归出口，递归出口是当你走到出口的时候，即i==n&&j==n。

此时遍历row和col，看看靶子上箭的数量是不是和aim_row,aim_col目标值对上。

如果对上了此时path里面存放的就是我们要的路径，打印出来即可。

如果没有对上就返回，不需要再进入下一节点了。

返回前注意需要回溯，消除维护操作。

 
void dfs(int i, int j) {
    visit[i][j] = true;
    row[i]++;
    col[j]++;
    path.push_back((i - 1) * n + (j - 1));

    if (i == n && j == n) {
        int flag = 1;
        for (int i = 1; i <= n; i++) {
            if (row[i] != aim_row[i] || col[i] != aim_col[i]) flag = 0;
        }
        if (flag == 1) {
            for (auto& x : path) cout << x << " ";
        }
                path.pop_back();
                row[i]--;
                col[j]--;
                visit[i][j] = false;
                return;
        
    }
    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
            dfs(x, y);
        }
    }

    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
}

 

代码1

7.

此时得到的代码如下，

 
#include <iostream>
#include<bits/stdc++.h>
using namespace std;

int n; // 定义n表示城堡地面是n×n个方格
vector<int> path; // 用于记录骑士的行走路径
vector<int> row; // 用于记录每行射出的箭的数量
vector<int> col; // 用于记录每列射出的箭的数量
vector<vector<int>> visit; // 记录某个格子是否被访问过
int dx[4] = { 1,-1,0,0 }; // 方向数组，用于实现上下左右移动
int dy[4] = { 0,0,1,-1 };
vector<int> aim_col; // 存储每列应该射出的箭的目标数量
vector<int> aim_row; // 存储每行应该射出的箭的目标数量

// 深度优先搜索（DFS）函数，用于尝试所有可能的路径
void dfs(int i, int j) {
    visit[i][j] = true; // 标记当前格子为已访问
    row[i]++; // 当前行的箭数增加
    col[j]++; // 当前列的箭数增加
    path.push_back((i - 1) * n + (j - 1)); // 将当前格子编号加入路径

    // 如果到达东南角，并且每行每列的箭数都符合目标
    if (i == n && j == n) {
        int flag = 1;
        for (int i = 1; i <= n; i++) {
            if (row[i] != aim_row[i] || col[i] != aim_col[i]) flag = 0;
        }
        if (flag == 1) {
            for (auto& x : path) cout << x << " "; // 如果路径有效，输出这条路径
        }
        path.pop_back();
        row[i]--;
        col[j]--;
        visit[i][j] = false;
        return;
    }

    // 尝试向四个方向移动
    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
            dfs(x, y);
        }
    }

    // 回溯，撤销当前步骤的影响
    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
}

int main() {
    cin >> n; // 读入n的大小
    aim_col.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> aim_col[i]; // 读入每列的目标箭数
    aim_row.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> aim_row[i]; // 读入每行的目标箭数

    row.resize(n + 1);
    col.resize(n + 1);
    visit = vector<vector<int>>(n + 1, vector<int>(n + 1));

    dfs(1, 1); // 从西北角开始进行深度优先搜索

    return 0;
}

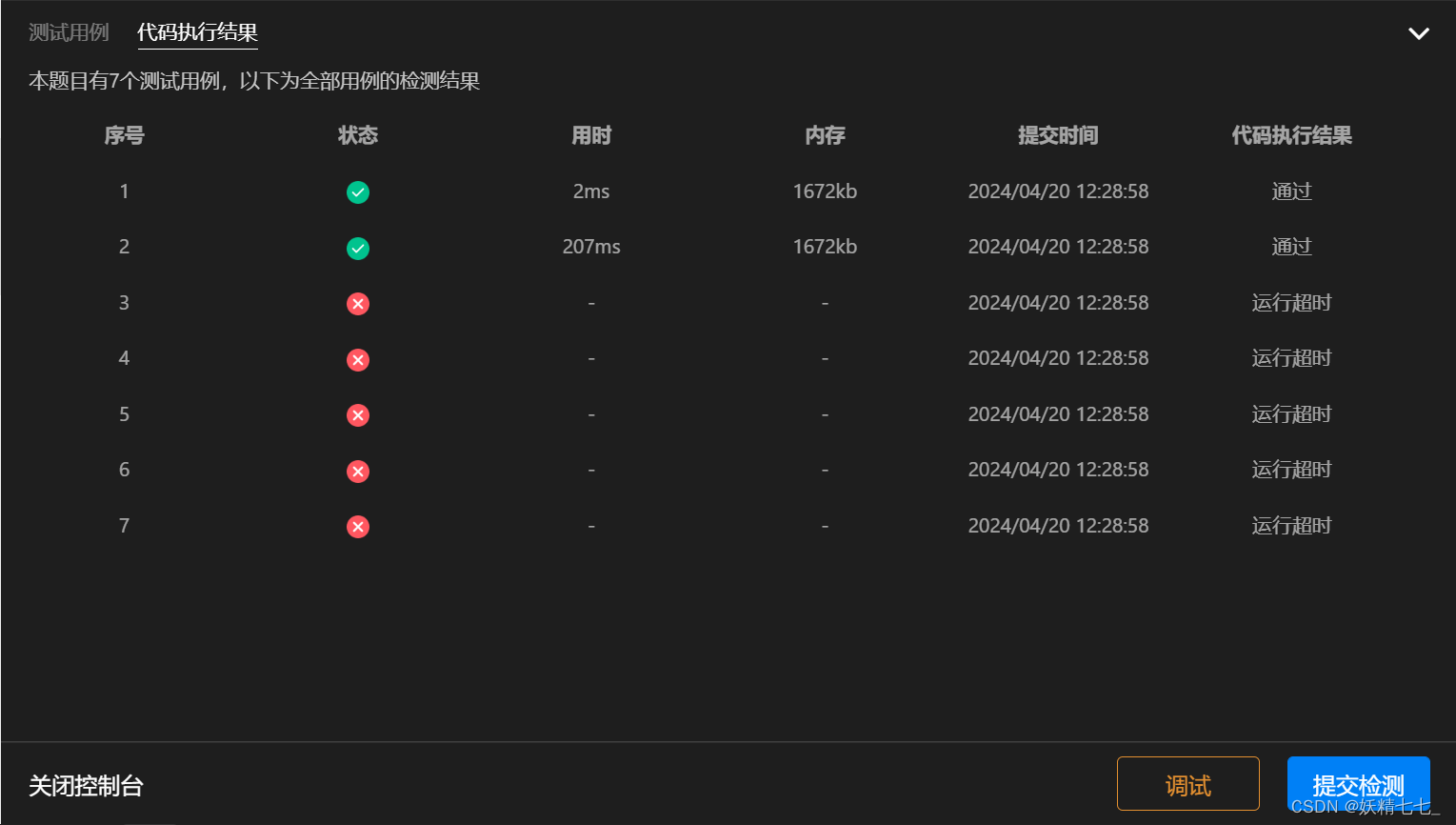
运行结果如下，

09945d723f644fc8a58e3ff7d6749755.png

剪枝1：唯一解找到即返回true（飞升）

8.

大部分运行超时，说明代码整体逻辑没有问题，但是剪枝操作没有做好。

重新思考剪枝操作。

题目中测试数据保证了路径的唯一性，说明我们只要找到了最终答案，就不需要回溯，后面的操作都不需要，找到最终答案就一路飞升回到第一层递归返回。

修改dfs的返回值，不使用void返回值，而使用int或者bool，意思是如果当前找到了就返回true，没有找到就返回false。

修改完返回值还需要修改进入下一层递归的代码，不能直接是dfs，而是if(dfs(x, y)) return true;。

如果返回值是true说明找到了，如果找到了什么都不用管，直接返回true。

每一层节点都接收这个信息，有没有完成工作，有没有找到路径？找到了就可以不用再工作了，直接返回。

还需要修改递归出口的逻辑，flag==1说明找到了，打印完路径后直接返回true。

 
int dfs(int i, int j) {
    visit[i][j] = true;
    row[i]++;
    col[j]++;
    path.push_back((i - 1) * n + (j - 1));

    if (i == n && j == n) {
        int flag = 1;
        for (int i = 1; i <= n; i++) {
            if (row[i] != aim_row[i] || col[i] != aim_col[i]) flag = 0;
        }
        if (flag == 1) {
            for (auto& x : path) cout << x << " ";
            return true;
        }
            path.pop_back();
            row[i]--;
            col[j]--;
            visit[i][j] = false;
            return;
    }
    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
             if(dfs(x, y)) return true;
        }
    }

    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
    
    return false;
}

 

代码2

9.

 
#include <iostream>
#include<bits/stdc++.h>
using namespace std;

int n; // 城堡地面为n×n个方格的大小
vector<int> path; // 存储骑士的行走路径
vector<int> row; // 每行射箭的次数
vector<int> col; // 每列射箭的次数
vector<vector<int>> visit; // 标记方格是否访问过
int dx[4] = { 1,-1,0,0 }; // x方向的移动：下，上，不动，不动
int dy[4] = { 0,0,1,-1 }; // y方向的移动：不动，不动，右，左
vector<int> aim_col; // 目标，每列应射箭的次数
vector<int> aim_row; // 目标，每行应射箭的次数

// 深度优先搜索（DFS）算法，i和j表示当前位置
int dfs(int i, int j) {
    visit[i][j] = true; // 标记当前方格为已访问
    row[i]++; // 当前行的射箭次数增加
    col[j]++; // 当前列的射箭次数增加
    path.push_back((i - 1) * n + (j - 1)); // 将当前方格的编号加入到路径中

    // 检查是否到达右下角，并且所有行和列的射箭次数都符合目标
    if (i == n && j == n) {
        int flag = 1; // 用于检查是否所有行和列的射箭次数都匹配
        for (int i = 1; i <= n; i++) {
            if (row[i] != aim_row[i] || col[i] != aim_col[i]) flag = 0;
        }
        if (flag == 1) {
            for (auto& x : path) cout << x << " "; // 如果匹配，输出路径
            cout << endl; // 输出换行
            return true; // 返回找到有效路径
        }
    }

    // 尝试四个可能的移动方向
    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
            if (dfs(x, y)) return true; // 递归调用dfs
        }
    }

    // 回溯，撤销当前步骤
    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;

    return false; // 没有找到有效路径
}

int main() {
    cin >> n;
    aim_col.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> aim_col[i]; // 输入每列的目标射箭次数
    aim_row.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> aim_row[i]; // 输入每行的目标射箭次数

    row.resize(n + 1);
    col.resize(n + 1);
    visit = vector<vector<int>>(n + 1, vector<int>(n + 1, false)); // 初始化访问标记数组

    dfs(1, 1); // 从(1,1)开始深度优先搜索

    return 0;
}

运行结果如下，

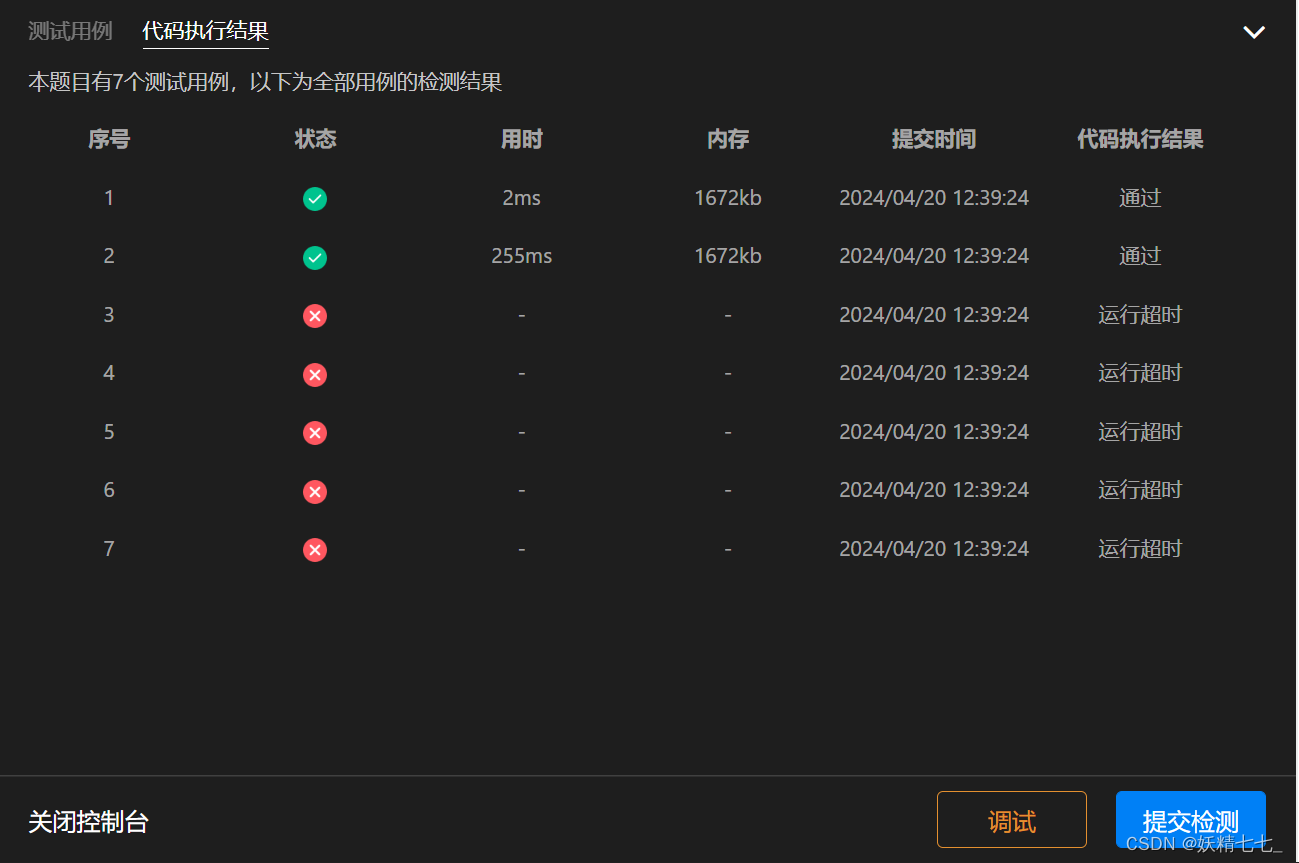
a94fedcc6cc74cd2bcb5c4451d3fd699.png

剪枝2：靶子箭数量小于目标靶子箭数量

10.

说明这个剪枝操作微不足道，没什么用。

继续思考其他剪枝操作，我们发现如果到了一个节点，如果row，col中有一个靶子的箭数量大于目标靶子的箭数量，后面的路径都不可能是最终答案。

因为靶子上箭的数量不可能减少只能增加，所以到出口之前，如果是正确路径，靶子数量一定小于目标靶子数量。

所以如果靶子箭数量大于目标靶子箭数量，直接返回。

 
int dfs(int i, int j) {
    visit[i][j] = true;
    row[i]++;
    col[j]++;
    path.push_back((i - 1) * n + (j - 1));

    int flag1 = 1;
    for (int i = 1; i <= n; i++) {
        if (row[i] > aim_row[i] || col[i] > aim_col[i]) {
            flag1 = 0;
            break;
        }
    }
    if (flag1 == 0) {
        path.pop_back();
        row[i]--;
        col[j]--;
        visit[i][j] = false;

        return false;
    }

    if (i == n && j == n) {
        int flag = 1;
        for (int i = 1; i <= n; i++) {
            if (row[i] != aim_row[i] || col[i] != aim_col[i]) {
                flag = 0;
                break;
            }
        }
        if (flag == 1) {
            for (auto& x : path) cout << x << " ";
            return true;
        }else{
        path.pop_back();
        row[i]--;
        col[j]--;
        visit[i][j] = false;

        return false;
    }
    }

    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
            if (dfs(x, y)) return true;
        }
    }

    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;

    return false;
}

 

代码3

 
#include <iostream>
#include<bits/stdc++.h>  // 引入常用库，包含STL等
using namespace std;

// 定义全局变量
int n;  // 地图大小
vector<int> path;  // 记录路径
vector<int> row;  // 记录每行走过的次数
vector<int> col;  // 记录每列走过的次数
vector<vector<int>> visit;  // 访问标记数组
int dx[4] = { 1,-1,0,0 };  // 方向数组，表示行的移动
int dy[4] = { 0,0,1,-1 };  // 方向数组，表示列的移动
vector<int> aim_col;  // 目标列的箭数
vector<int> aim_row;  // 目标行的箭数

// 深度优先搜索函数
int dfs(int i, int j) {
    visit[i][j] = true;  // 标记当前单元格已访问
    row[i]++;  // 增加当前行的计数
    col[j]++;  // 增加当前列的计数
    path.push_back((i - 1) * n + (j - 1));  // 记录路径

    int flag1 = 1;
    // 检查所有行列是否满足条件
    for (int i = 1; i <= n; i++) {
        if (row[i] > aim_row[i] || col[i] > aim_col[i]) {
            flag1 = 0;
            break;
        }
    }
    if (flag1 == 0) {  // 如果条件不满足，则回退操作
        path.pop_back();
        row[i]--;
        col[j]--;
        visit[i][j] = false;
        return false;
    }

    // 检查是否到达最后一个方格
    if (i == n && j == n) {
        int flag = 1;
        for (int i = 1; i <= n; i++) {
            if (row[i] != aim_row[i] || col[i] != aim_col[i]) {
                flag = 0;
                break;
            }
        }
        if (flag == 1) {  // 如果满足最终条件，输出路径
            for (auto& x : path) cout << x << " ";
            return true;
        } else {  // 否则，进行回退操作
            path.pop_back();
            row[i]--;
            col[j]--;
            visit[i][j] = false;
            return false;
        }
    }

    // 遍历四个方向
    for (int k = 0; k < 4; k++) {
        int x = i + dx[k], y = j + dy[k];
        if (x >= 1 && x <= n && y >= 1 && y <= n && !visit[x][y]) {
            if (dfs(x, y)) return true;
        }
    }

    // 回退操作
    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
    return false;
}

int main() {
    cin >> n;
    aim_col.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> aim_col[i];  // 输入北边靶子箭数
    aim_row.resize(n + 1);
    for (int i = 1; i <= n; i++) cin >> aim_row[i];  // 输入西边靶子箭数

    row.resize(n + 1);
    col.resize(n + 1);
    visit = vector<vector<int>>(n + 1, vector<int>(n + 1));  // 初始化访问矩阵

    dfs(1, 1);  // 从(1,1)开始搜索

    return 0;
}

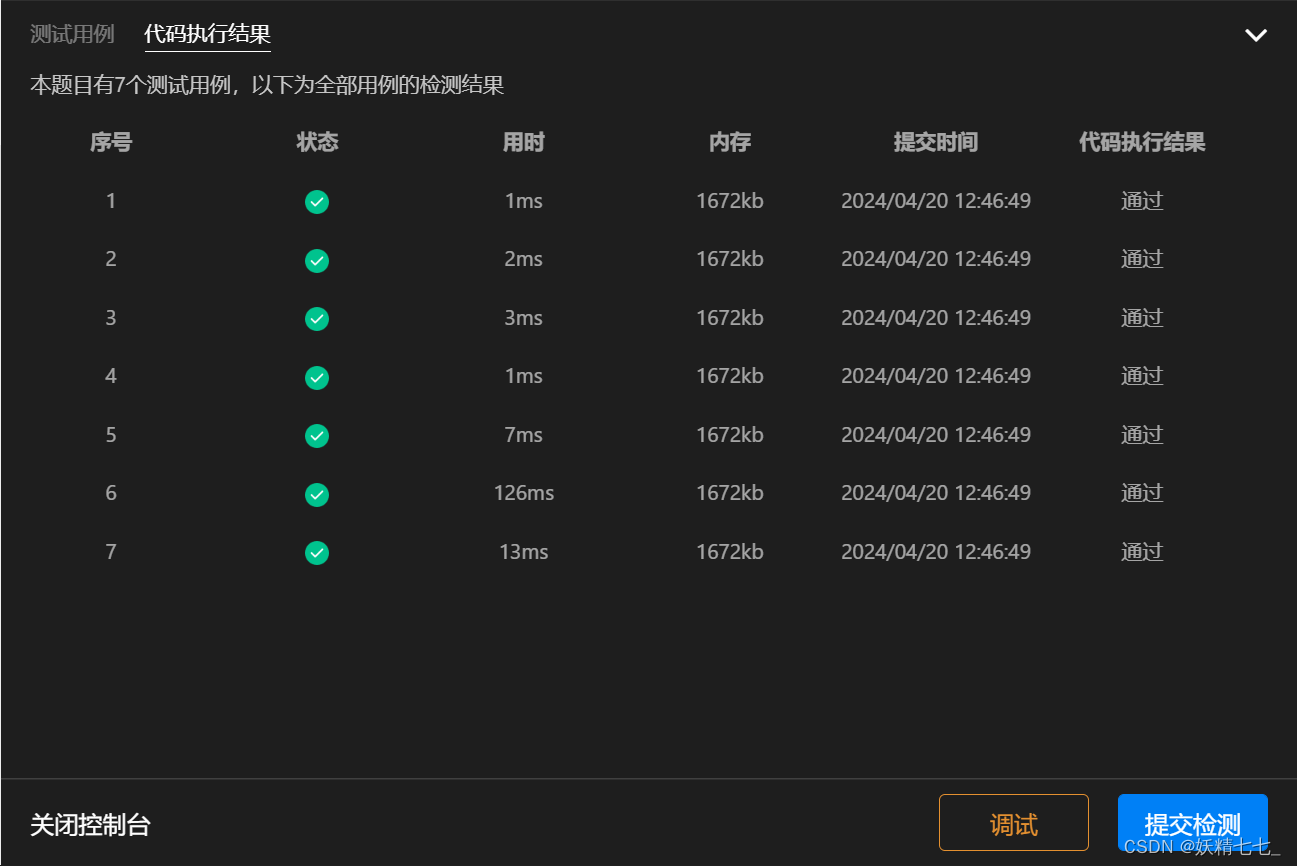
72a4030d74204f56b86d822e926b7774.png

总结结论

1.

递归函数dfs，用同样的函数完成相同的逻辑问题，但是需要用其他遍历辅助判断当前位于那个节点。

vector<int> path;

vector<int> row;

vector<int> col;

vector<vector<int>> visit;

(i,j）

以上都是当前节点的信息。

2.

每一次进入dfs维护当前节点信息，每一次出去之前回溯，消除维护的信息。

 
void dfs(int i, int j) {
    visit[i][j] = true;
    row[i]++;
    col[j]++;
    path.push_back((i - 1) * n + (j - 1));//数学推导不细说，找规律
    //添加主要逻辑
    path.pop_back();
    row[i]--;
    col[j]--;
    visit[i][j] = false;
}

 

3.

如果只需要找唯一解，找到即返回，找到就不用工作，找到就飞升。

修改返回值，进入下一层逻辑，出口逻辑。

7401f170df974efcb1dc440636a9fd40.png

4.

剪枝操作提前返回，注意返回之前一定要回溯，也就是消除维护当前节点信息的操作！！！

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

 

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

 

谢谢您的支持，期待与您在下一篇文章中再次相遇！

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1620571.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

短信视频提取批量工具，免COOKIE，博主视频下载抓取，爬虫

短信视频提取批量工具，免COOKIE，博主视频下载抓取，爬虫

痛点&#xff1a;关于看了好多市面的软件&#xff0c;必须要先登录自己的Dy号才能 然后找到自己的COOKIE 放入软件才可以继续搜索&#xff0c;并且无法避免长时间使用 会导致无法正常显示页面的问题。 有没有一种方法 直接可以使用软件&#xff0c;不用设置的COOKIE的方法呢 …
阅读更多...
对于地理空间数据，PostGIS扩展如何在PostgreSQL中存储和查询地理信息？

对于地理空间数据，PostGIS扩展如何在PostgreSQL中存储和查询地理信息？

文章目录 一、PostGIS扩展简介二、PostGIS存储地理空间数据1. 创建空间数据表2. 插入空间数据 三、PostGIS查询地理空间数据1. 查询指定范围内的地理空间数据2. 计算地理空间数据之间的距离3. 对地理空间数据进行缓冲区分析 四、总结 地理空间数据是指描述地球表面物体位置、形…
阅读更多...
开源社区与开发者的故事

开源社区与开发者的故事

开源社区与开发者的故事 什么是开源社区你参加开源社区的主要目的你是否在开源社区中贡献&#xff0c;或者开源自己的项目&#xff1f;你认为个人开发者是否应该从开源中获利&#xff1f;如果是&#xff0c;该如何获利&#xff1f; 今天要谈及的主题是开源社区&#xff0c;那么…
阅读更多...
2024年新算法-牛顿-拉夫逊优化算法(NRBO)优化BP神经网络回归预测

2024年新算法-牛顿-拉夫逊优化算法(NRBO)优化BP神经网络回归预测

亮点&#xff1a; 输出多个评价指标&#xff1a;R2&#xff0c;RMSE&#xff0c;MSE&#xff0c;MAPE和MAE 满足需求&#xff0c;分开运行和对比的都有对应的主函数&#xff1a;main_BP, main_NRBO, main_BPvsBP_NRBO&#xff0c;并且详细中文注释 方便快捷&#xff1a;替换…
阅读更多...
打破企业差旅管理困局，让金融CEO眼前一亮的出行方案

打破企业差旅管理困局，让金融CEO眼前一亮的出行方案

在国内券商投行部工作是怎样一种体验&#xff1f; “长期出差&#xff0c;而且出长差&#xff0c;时常让人有漂泊的孤独感。”这是某问答平台上的高赞回答的第一条。 对金融人来说&#xff0c;说走就走的旅行可能根本没有什么吸引力&#xff0c;时刻准备着说走就走的出差才是生…
阅读更多...
MVCC的执行原理

MVCC的执行原理

MVCC的执行原理 MVCC简介事务的隔离级别MVCC作用当前读和快照读MVCC实现原理Undo LogUndo Log 版本链Read View判断方法判断规则 小结 MVCC简介 MVCC&#xff08;Multi-Version Concurrency Control&#xff09;是一种并发控制机制&#xff0c;用于解决数据库并发访问中&#…
阅读更多...
pyqt 动态更换表头和数据

pyqt 动态更换表头和数据

目录 pyqt 动态更换表头和数据代码 效果图&#xff1a; pyqt 动态更换表头和数据代码 from PyQt5.QtGui import QColor, QBrush from PyQt5.QtWidgets import QApplication, QTableWidget, QVBoxLayout, QWidget, QPushButton, QTableWidgetItemclass Example(QWidget):def _…
阅读更多...
如何诊断并解决PostgreSQL中的磁盘空间不足问题？

如何诊断并解决PostgreSQL中的磁盘空间不足问题？

文章目录 诊断磁盘空间不足问题1. 检查服务器磁盘空间2. 检查PostgreSQL数据目录大小3. 检查PostgreSQL中的大表和大对象 解决磁盘空间不足问题1. 清理不必要的文件和日志2. 清理或压缩大表和大对象3. 扩展磁盘容量4. 优化数据库配置和查询 在使用PostgreSQL数据库时&#xff0…
阅读更多...
华为云实验 -- 对云硬盘数据盘进行备份

华为云实验 -- 对云硬盘数据盘进行备份

文章目录 备份Linux系统备份1.购买Linux操作系统的ESC(云服务器)2.挂载数据盘--初始化--分区--格式化2.1.点击"远程登录"a.查看/dev/vdb数据盘b.新建主分区/dev/vdb1 2.2.查看新建分区大小,分区格式信息a.确定之前的分区操作是否正确b.确认完成后&#xff0c;将分区结…
阅读更多...
【MATLAB源码-第32期】基于matlab的通信及雷达中常用伪随机码m序列的仿真。

【MATLAB源码-第32期】基于matlab的通信及雷达中常用伪随机码m序列的仿真。

操作环境&#xff1a; MATLAB 2022a 1、算法描述 M序列&#xff0c;也称为最大长度序列或者伪随机序列&#xff0c;是一种特殊的二进制序列。它的特点是在有限的长度内&#xff0c;尽管它是伪随机的&#xff0c;但它会在特定的周期内不重复地循环。 在数学上&#xff0c;M序…
阅读更多...
利用fft算法重写公式并理解频率和像素变化率的关系(完美解决问题)

利用fft算法重写公式并理解频率和像素变化率的关系(完美解决问题)

算法我就不贴了。算法就是算法导论的内容。 我直接写推导过程。 假设变化率为f(n1)-f(n) 首先计算二进制数&#xff0c;这里我假设为3位二进制。 例如:f(5)-f(4)&#xff0c; 5和4的二进制为101,100。所以逆序数为101&#xff0c;001 101对应的频率为5, 001对应的频率为1…
阅读更多...
力扣HOT100 - 236. 二叉树的最近公共祖先

力扣HOT100 - 236. 二叉树的最近公共祖先

解题思路&#xff1a; dfs 节点p,q异侧时&#xff0c;节点root为它们的公共祖先。 class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root null || p root || q root) return root;TreeNode left lowestCommonAncest…
阅读更多...
max各种相机导出到ue4匹配镜头的工具集

max各种相机导出到ue4匹配镜头的工具集

总览 rollout export_UE4Cam_v2 "导出UE4Cam_v2:半自动" width:200 height:120(HyperLink explain "在打开的max文件中使用" pos:[25,12] width:200 height:15 color:(color 255 155 0) GroupBox grp1 "要导出的相机名" pos:[5,28] width:179 …
阅读更多...
NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections

NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections

NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections(野外的 NERF: 用于无约束照片采集的神经辐射场&#xff09; Abstract 我们提出了一种基于学习的方法来合成新的视图的复杂场景使用只有非结构化的收集野生照片。我们建立在神经辐射场(neRF)的…
阅读更多...
深度学习算法简介（一）

深度学习算法简介（一）

目录 ⛳️推荐 前言 1、深度神经网络&#xff08;DNN&#xff09; 2、卷积神经网络&#xff08;CNN&#xff09; 3、残差网络&#xff08;ResNet&#xff09; 4、LSTM&#xff08;长短时记忆网络&#xff09; 5、Word2Vec 6、Transformer 7、生成对抗网络&#xff08;…
阅读更多...
MySQL常见的约束

MySQL常见的约束

什么是约束&#xff1f; 限制&#xff0c;限制我们表中的数据&#xff0c;保证添加到数据表中的数据准确和可靠性&#xff01;凡是不符合约束的数据&#xff0c;插入时就会失败&#xff0c;插入不进去的&#xff01; 比如&#xff1a;学生信息表中&#xff0c;学号就会约束不…
阅读更多...
【IC设计】奇数分频与偶数分频 电路设计（含讲解、RTL代码、Testbench代码）

【IC设计】奇数分频与偶数分频 电路设计（含讲解、RTL代码、Testbench代码）

文章目录 原理分析实现和仿真偶数分频的电路RTL代码偶数分频的电路Testbench代码偶数分频的电路仿真波形占空比为50%的三分频电路RTL代码占空比为50%的三分频电路Testbench代码占空比为50%的三分频电路仿真波形 参考资料 原理分析 分频电路是将给定clk时钟信号频率降低为div_c…
阅读更多...
北斗卫星助力农业生产精准播种

北斗卫星助力农业生产精准播种

北斗卫星助力农业生产精准播种 随着现代化农业的不断进步&#xff0c;高科技技术的融合已成为推动农业生产向前发展的重要动力。其中&#xff0c;北斗卫星导航系统&#xff08;BDS&#xff09;的应用&#xff0c;特别是在农业播种领域的利用&#xff0c;标志着农作物种植方式的…
阅读更多...
私域运营的基础是什么?

私域运营的基础是什么?

私域运营是指在自有平台上进行的一系列运营活动&#xff0c;旨在建立和维护与用户的深度互动关系&#xff0c;提升用户忠诚度和品牌影响力。相比于传统的广告投放和推广方式&#xff0c;私域运营更加注重与用户的沟通和互动&#xff0c;通过提供有价值的内容和个性化的服务&…
阅读更多...
业务复习知识点Oracle查询

业务复习知识点Oracle查询

业务数据查询-1 单表查询 数据准备 自来水收费系统建表语句.sql 简单条件查询 精确查询 需求 &#xff1a;查询水表编号为 30408 的业主记录 查询语句 &#xff1a; select * from t_owners where watermeter 30408; 查询结果 &#xff1a; 模糊查询 需求 &#xff1a;查询业…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023