利用fft算法重写公式并理解频率和像素变化率的关系(完美解决问题)

news2024/12/25 0:18:18

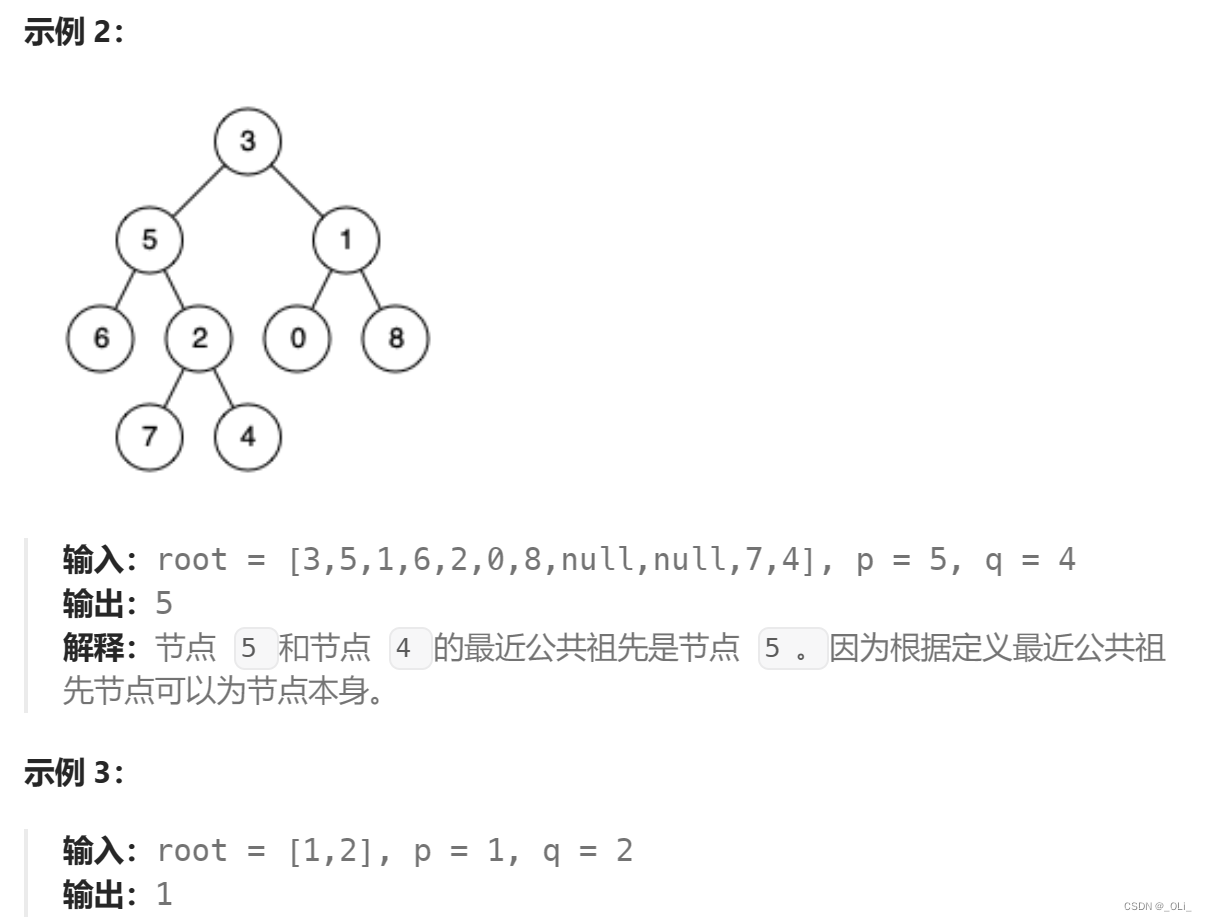
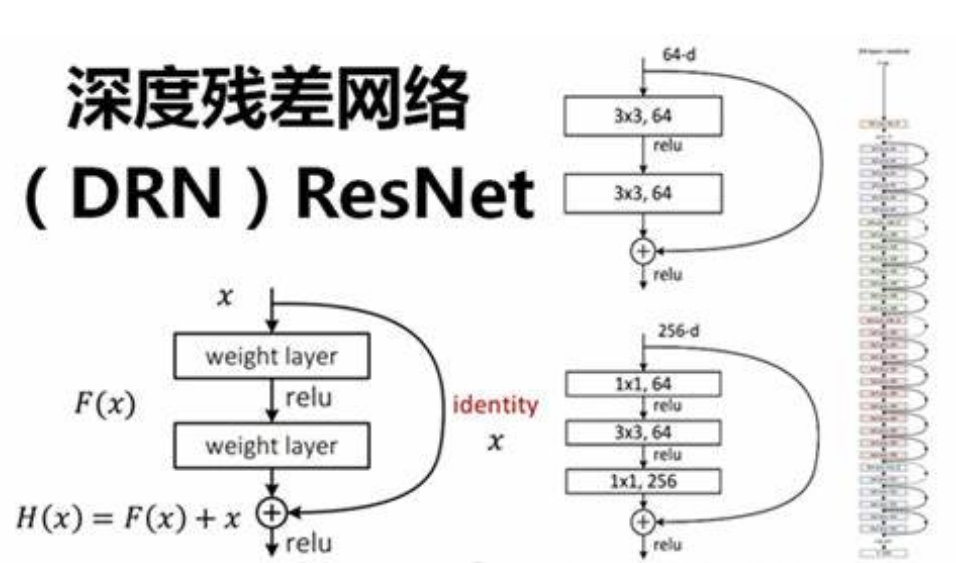
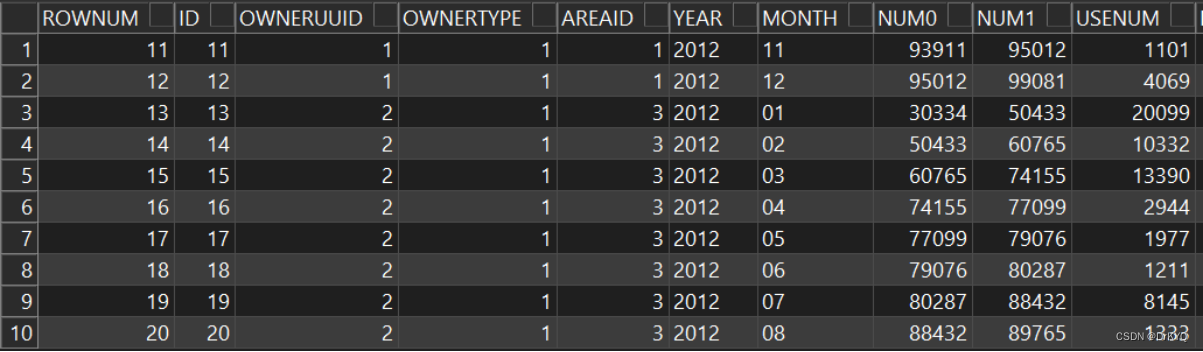
算法我就不贴了。算法就是算法导论的内容。

我直接写推导过程。

假设变化率为f(n+1)-f(n)

首先计算二进制数，这里我假设为3位二进制。

例如:f(5)-f(4)，

5和4的二进制为101,100。所以逆序数为101，001

101对应的频率为5, 001对应的频率为1。书上的代码是fft变换，这里是反变换，所以1是顺时针转动。

这里高频的只有5，所以先计算5的转动过程。

我先介绍一下Fk转动过程，首先，最高位为1的Fk的都这样转动，第一次转动为 $\pi$ ，第二次转动为 $\pi/2$ ，第k次转动为 $\pi/2^{k}$ ，总共会转动 $\log_{2} N$ 次。至于转动的方向是根据正变换还是反变换，因为这里是反变换，所以1是顺时针转动，0是不转动。如果最高位不为1，就不转动，次高位为1，开始转动 $\pi/2$ ，继续按照上面的规律转动，每次转动为当前层级2^(N-n)的 $\pi/2^{N-n}$ （从第零层开始）,n为当前层级。

转动过程在生成的fn中起什么作用呢？我只能说是做加减组合之后就是生成fn的分量了，如何组合呢？关键就是符号的确定了。

符号的确定方式是这样的：

以ai在yj中的符号确定为例，

首先是a4在y5中的符号

100与101=100，经历了负正正，所以为负。

a6在y4中的符号

110与001=000，所以为正。

a3在y4中的符号

011与001=001，为负。

ai的下标的二进制数和yj的下标的二进制数的逆序数相与，出现偶数个1为正，奇数个1为负。

这样我就获得了傅里叶反变换的计算公式了。

总结如下:

1..首先是计算输入的ai在复平面的转动角度 $\theta_{i}$ ，即是 $ai*e^{\theta_{i} }$ 。假设N恰好是2次方幂，设长度为m= $\log_{2} N$ 。假设下标i的二进制数为x1x2....xm。

$\theta_{i} =\sum_{j=1}^{m}(2\pi/2^{j})*xj$ ,当xj=1，是累加进去的，xj=0就没有加。

2.,接着是确定 $ai*e^{\theta_{i} }$ 符号。

假设fj的下标j的二进制数为y1y2...ym。所以逆序数为ym...y2y1

x1x2....xm和ym...y2y1做与运算。统计1的个数，为奇数个，则为负号，为偶数个为正号，设为 $\delta (fj,ai)$ 。

3.,所以fj= $\sum_{i=0}^{N-1}$ $\delta (fj,ai)$ * $ai*e^{\theta_{i} }$ 。

但是这个和频率，变化率有什么关系？

因为频率是ai的下标i。所以f(n+1)-f(n)表明，n+1和n的二进制中末位一个是1，一个是0，所以逆序数中总有一个是大的，一个是小的。其次需要知道的是 $ai*e^{\theta_{i} }$ $ai*e^{\theta_{i} }$ 在输入ai的时候都是确定的了，跟j无关，而跟j有关的是符号 $\delta (fj,ai)$ ，

所以f(n+1)-f(n)= $\sum_{i=0}^{N-1}$ [ $\delta (f(n+1),ai)$ - $\delta (f(n),ai)$ ]* $ai*e^{\theta_{i} }$ 。因为是统计1的个数，假设前面三个1，后面一个1，那就是2个了，那就是做了异或操作。

如果下标n为y1y2...011..1，则n+1为y1y2...100..0，异或为00...11..1

如果下标n为y1y2...100..0，则n+1为y1y2...100..1，异或为00...00..1

设异或结果的逆序数为gn，gn与ai的下标相与之后统计1的个数，设为h(n,i)

所以f(n+1)-f(n)= $\sum_{i=0}^{N-1}$ h(n,i)* $ai*e^{\theta_{i} }$ 。观察发现逆序数都是高位的。因为是与ai的下标i相与，统计1的个数，这意味着i的二进制数中的较低位置不能决定ai的符号，具体的情况跟n的值有关。而符号关系到最终的数值大小，大部分符号为一致的话，最终的向量值更大一些，虽然也跟幅度有关，但是这里输入ai都已经固定了，不需要考虑了。

所以我该怎么说呢？像素变化率确实跟频率有关，但是频率的较高处跟n的值有关，如果理想的话，i与10...00相与统计1的个数，那么所有的高频处一致为负号。最差的情况是11...1和i相与，符号完全由i决定，但是这种情况下，n值为011..111，这表示是在图像的点列中的中间处。只有一个像素点如此，其次最差的是0011..111，继续下去，其他的情况都要好很多。

我终于完成了频率和像素变化的说明了。居然是跟二进制位有关。

算错了。要修改一下。因为只是符号不同而已，可能的值为2,0，-2。

所以f(n+1)-f(n)= $\sum_{i=0}^{N-1}$ [ $\delta (f(n+1),ai)$ - $\delta (f(n),ai)$ ]* $ai*e^{\theta_{i} }$ 。

如果下标n为y1y2...011..1，则n+1为y1y2...100..0，

如果下标n为y1y2...100..0，则n+1为y1y2...100..1。

n=y1y2...ym011..1的逆序为1...110ym..y2y1，n+1逆序为0...001ym...y2y1，

n=y1y2...ym100..0的逆序为0...001ym..y2y1，n+1逆序为1...001ym...y2y1，

先看第一种情况:

0...001ym..y2y1与i=x1x2...xM相与然后异或为: $\bigoplus_{j=1}^{m}(x(M-j+1)*yj)\bigoplus x(M-m)$ , $\bigoplus$ 是异或操作，若结果为1则是负号，结果为0，则是正号。

1...110ym..y2y1与i=x1x2...xM相与然后异或为: $\bigoplus_{j=1}^{m}(x(M-j+1)*yj)\bigoplus_{j=1}^{M-m-1} x(j)$ 。

对比发现在低位的地方异或方式是一样的，设h(1)=-1, h(0)=1。h对于异或操作有h(a $\bigoplus$ b)=h(a)*h(b)。所以

$h(\bigoplus_{j=1}^{m}(x(M-j+1)*yj)\bigoplus x(M-m))=h(\bigoplus_{j=1}^{m}(x(M-j+1)*yj))*h(x(M-m))$

$h(\bigoplus_{j=1}^{m}(x(M-j+1)*yj)\bigoplus_{j=1}^{M-m-1} x(j))=h(\bigoplus_{j=1}^{m}(x(M-j+1)*yj))*h(\bigoplus_{j=1}^{M-m-1} x(j))$

这看起来单个位置n的符号也是跟频率i的低位有关，频率的高位反而不影响。但是ai的符号做了减法之后发现，低位的符号作用是一样的，决定ai符号的是高位x1x2..x(M-m)。

再看第二种情况:

情况也是一样的，我就不写了。这能说明什么呢？这说明的是低频对符号有一致的影响，高频对符号有不一致的影响。对于变化率来说，如果符号是一致变化的，那就没变化，所以高频能改变变化率。观察上面的n的二进制和逆序，发现一致变化的区域在n的低位，根据低位的个数决定，位数越低，如果改变n的低位函数值f(n0),越低表示n0越接近n，那么只越对高频的i的函数值F(i)的符号无影响，但是影响各个频率的幅度值。

最好的情况是n=011..1, n+1=100..0。n逆=1..110，n+1逆=0..001。完全由i的每个分量决定了符号。这表示图像中间的一个像素点在修改任意频率i的函数值ai的时候，变化率是由各种频率决定的。实际上变化率我之前分析过了，频率和幅度都起作用，但是我之前分不清高频和低频起的作用的区别，这里就能说明在不同的位置n，由不同的频率i起作用，甚至较低频率是不起作用的。

最差的情况是n=100..0, n+1=100..1。n逆=0..001，n+1逆=1..001。完全由i的高频分量决定了符号。这表示图像中间的一个像素点只在修改高频率i的函数值ai的时候，变化率几乎是由高频决定的。

最后我就

n=y1y2...ym011..1的逆序为1...110ym..y2y1，n+1逆序为0...001ym...y2y1，

n=y1y2...ym100..0的逆序为0...001ym..y2y1，n+1逆序为1...001ym...y2y1，

给出一个简单的解释:

这里，因为在空间n位置的局部范围内，ym..y2y1不会改变，所以逆序与i相与，得到的符号也不会改变。假设高频的值全为0，那么意味着f(n)在n的局部的值没有变化。因为高频为0，而低频的值ai和旋转角度都是固定的，唯一变化的是符号，但是在n的局部范围内符号没有变化，则f(n)在n的局部的值没有变化，根据我的这个公式:

fj= $\sum_{i=0}^{N-1}$ $\delta (fj,ai)$ * $ai*e^{\theta_{i} }$ 。

如何理解像素剧烈变化呢？反正基本上是空间的局部范围内n变化的时候，由于逆序之后符号变化是在高频跳到中频范围反复的，所以如果这个范围内ai不为0，那么图像像素的变化率大。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1620554.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！