实验6贪心算法-活动安排问题和背包问题
实验目的:
- 理解贪心算法的基本思想
- 运用贪心算法解决实际问题
实验内容:
- 采用贪心方法编程实现以下问题的算法
1.如何安排下列活动使得使用的活动场所最少,并给出具体的安排方法。
| 活动 | a | b | c | d | e | f | g |
| 开始 | 0 | 3 | 4 | 9 | 7 | 1 | 6 |
| 完成 | 2 | 7 | 7 | 11 | 10 | 5 | 8 |
2.现有一个容量为50的背包和三个物品,它们的重量分别是10,20,30,价值分别为60,100,120,如何装入物品使背包装满,且装入背包的物品总价值最大。
实验步骤:
-
活动安排问题
-
def greedy_activity_selector(start, finish): activities = sorted(range(len(finish)), key=lambda x: finish[x]) chosen_activities = [activities[0]] last_finish_time = finish[activities[0]] for i in activities[1:]: if start[i] >= last_finish_time: chosen_activities.append(i) last_finish_time = finish[i] return chosen_activities start = [0,3,4,9,7,1,6] finish = [2,7,7,11,10,5,8] selected = greedy_activity_selector(start, finish) print("Selected activities:", selected)
-
背包问题
-
def greedy_knapsack(values, weights, capacity): value_per_weight = [v/w for v, w in zip(values, weights)] items = sorted(range(len(values)), key=lambda i: value_per_weight[i], reverse=True) max_value = 0 fractions = [0] * len(values) for i in items: if weights[i] <= capacity: fractions[i] = 1 max_value += values[i] capacity -= weights[i] else: fractions[i] = capacity / weights[i] max_value += values[i] * capacity / weights[i] break return max_value, fractions values = [60, 100, 120] weights = [10, 20, 30] capacity = 50 max_value, fractions = greedy_knapsack(values, weights, capacity) print("Maximum value in knapsack:", max_value) print("Fractions of items taken:", fractions)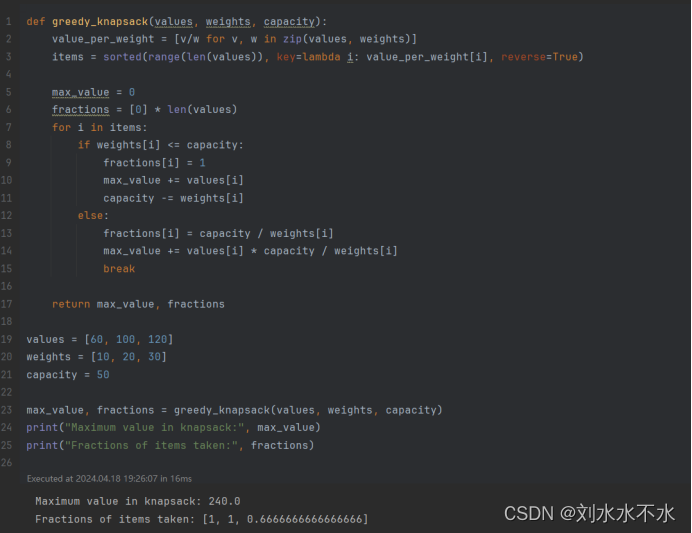
实验感想:
贪心算法在这两个问题上的应用非常直观和简洁。它不需要复杂的回溯或穷举,只需按照某种策略选择当前最优解,这大大简化了问题求解的过程。贪心算法在活动安排和分数背包问题上的效率非常高,这是因为它们都拥有贪心选择性质和最优子结构。但在其他背包问题(如0-1背包问题)上,贪心算法可能无法找到最优解,这体现了算法效率和效果之间的平衡。
在背包问题中,将问题转化为分数背包问题,使我们能够应用贪心策略。这种问题转化的能力是解决复杂问题的关键。通过实验,我更深刻地理解了贪心算法适用的问题类型。贪心算法适用于那些局部最优解能导致全局最优解的问题。通过编写代码实现这些算法,我不仅加深了对算法理论的理解,还提高了编程能力和调试技巧。解决这类问题需要良好的逻辑思维和算法设计能力。实验过程中,我学会了如何分析问题、设计算法,并将这些算法转化为代码。