Algorithm
本周的算法题为 21. 合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
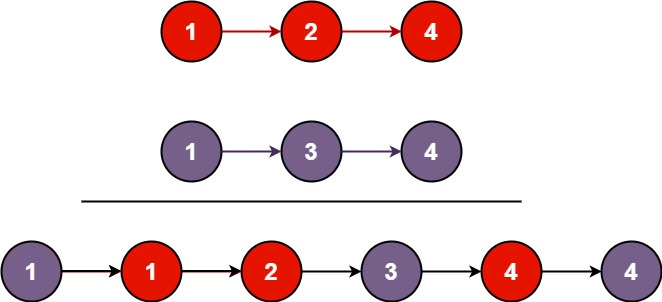
输入:list1 = [1,2,4], list2= [1,3,4]
输出:[1,1,2,3,4,4]
实现代码如下:
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} list1
* @param {ListNode} list2
* @return {ListNode}
*/
const mergeTwoLists = function(list1, list2) {
if (list1 === null) {
return list2;
} else if (list2 === null) {
return list1;
} else if (list1.val < list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
} else {
list2.next = mergeTwoLists(list1, list2.next);
return list2;
}
};
解题思路:
比较两个链表的头节点,将较小的头节点作为合并后的链表的头节点,然后递归地将剩余的部分合并。
-
首先,判断两个链表是否有空的情况,如果其中一个链表为空,说明另一个链表就是合并后的链表,直接返回。 -
接着,比较两个链表的头节点,将较小的头节点作为合并后的链表的头节点。 -
对于较小头节点所在的链表,将其头节点的下一个节点与另一个链表进行合并,得到的结果作为较小头节点的下一个节点。 -
返回较小头节点作为合并后的链表的头节点。 -
重复以上步骤,直到两个链表的所有节点都被合并。
Review
UN warns of environmental e-waste catastrophe - Breaking News English Lesson
联合国向全球消费者发出了严厉警告。我们丢弃的电子产品数量已经造成了“环境灾难”。我们正在处理创纪录数量的“电子垃圾”。联合国将电子产品定义为任何带插头或电池的物品,并且通常含有有毒化学物质和物质,如铅和汞。电子垃圾包括被丢弃的手机、冰箱和电子烟。联合国全球电子垃圾监测器报告称,在2022年,全球产生了令人震惊的6200万吨电子垃圾。CNN表示,这些垃圾“可以填满超过150万辆40吨重的卡车,如果把它们挨个贴在一起,可以...绕过赤道”。
大多数电子垃圾来自发达国家。其中很多被发送到较贫穷的国家进行回收。然而,这些国家缺乏技术和资源以最大程度地减少环境破坏地处理电子垃圾。庞大的垃圾量造成了大量的健康问题。被倾倒的电子产品正在污染河流和海洋。去年有令人不安的58吨汞进入了环境。其中一部分进入了食物链。联合国指责制造商“缺乏责任心”,因为他们未能对其产品的命运负责。它还指责消费者,称“购买电子产品只需点击几下”,但“处理它们却更加困难”。
Tip
链表(LinkedList)是一种常见的数据结构,它由一系列节点组成,每个节点包含两部分:数据和指向下一个节点的引用。
常见的有单向链表和双向链表,单向链表中的每个节点只有一个指向下一个节点的引用,双向链表中每个节点都有两个引用,分别指向前一个节点和后一个节点。
链表的实现原理,主要依靠节点之间的引用关系。链表的头部指向第一个节点,而最后一个节点的指针指向 null。这样,当需要遍历链表时,只需从头部开始,依次沿着指针向下移动即可。
举个例子,假设我们有一个单向链表,其中包含节点 A、B、C 和 D,它们依次相连:
A -> B -> C -> D -> null
如果要查询链表中的某个节点,需要从头节点开始,沿着指针依次移动,直到找到目标节点或者到达链表末尾。
如果要删除或者插入节点,则需要调整相邻节点之间的引用关系,以保持链表的连续性。
与 ArrayList 相比,LinkedList 在查找和修改操作方面效率较低,因为需要遍历整个链表才能找到目标元素,但在增加和删除操作方面效率更高,因为不需要移动元素。
Share
循环论证是一种逻辑错误,具体表现为用来证明论题的论据本身的真实性要依靠论题来证明。换句话说,就是用论点去证明论据,再用论据来证明论点,这构成了一个无法打破的循环。比如,“真是奇怪,都说票好难抢,但是为什么动车上的人全都买到票了。”
本文由 mdnice 多平台发布