数学一直被认为是科学的基石,对于推动技术进步和解决现实世界问题具有重要意义。然而,传统的数学问题解决方式正面临着数字化转型的挑战。MLMs的出现,预示着数学学习和研究方式的一次革命。
MLMs,包括预训练语言模型(PLMs)和大语言模型(LLMs),已经成为数学问题解决领域的新星。这些模型通过在大量数学数据集上的预训练和微调,展示了在数学问题解决上的巨大潜力。
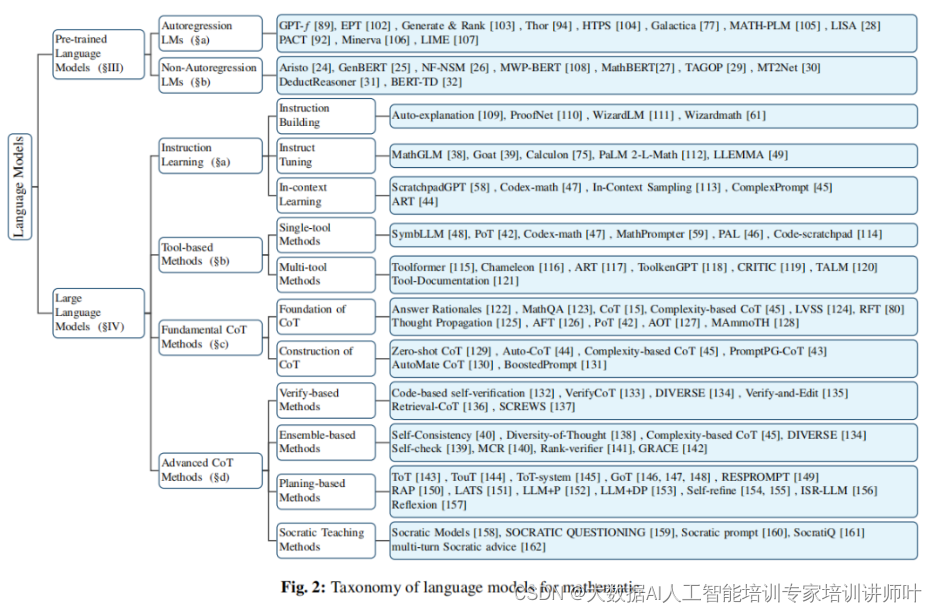
预训练语言模型是通过在大量文本数据上进行预训练来构建的,目的是让模型学习语言的基本结构和语义。这些模型通常使用无监督学习技术,如掩码语言建模(Masked Language Modeling, MLM),预测文本中随机掩盖(Masked)的部分。以下是一些著名的PLMs:
-
BERT (Bidirectional Encoder Representations from Transformers): 由Google开发,BERT通过双向注意力机制来捕捉文本中的上下文信息。
-
RoBERTa (A Robustly Optimized BERT Pretraining Approach): RoBERTa是BERT的一个改进版本,通过更有效的训练策略和更大的训练数据集来提高模型的性能。
-
BART (Facebook's BART): BART是一个基于Transformer的序列到序列模型,它在多种文本摘要任务上表现出色。
-
GPT (Generative Pre-trained Transformer): 由OpenAI开发,GPT系列模型专注于生成文本,能够生成连贯且语义上合理的文本序列。
这些模型在预训练后,通常需要通过微调(Fine-tuning)来适应特定的下游任务,如情感分析、文本分类或数学问题解答。
大语言模型是具有数十亿甚至数千亿参数的语言模型,它们能够处理和生成极其复杂的文本。这些模型的规模和复杂性使它们在多种自然语言处理任务上取得了前所未有的性能。以下是一些著名的LLMs:
-
GPT-3: 由OpenAI开发,GPT-3是一个具有1750亿参数的模型,它在多种任务上展示了强大的性能,包括文本生成、翻译和问答。
-
PaLM (Pathways Language Model): 由Google开发,PaLM是一个具有540亿参数的模型,它在多任务学习和少样本学习方面表现出色。
-
LMM (Large Multimodal Model): LMM是一个多模态模型,能够处理文本、图像和视频,为多模态任务提供了新的解决方案。
-
LLaMA (Large Language-Model Auxiliary Memory): LLaMA是一个开源的大语言模型,专注于在有限的计算资源下实现高效的性能。
LLMs的一个关键特点是它们能够在给定一些示例(即使是少量)的情况下学习执行复杂的任务,这被称为“少样本学习”或“零样本学习”。此外,它们还能够通过“链式思考”(Chain-of-Thought)机制来解决需要多步逻辑推理的问题。
在数学语言模型的背景下,PLMs和LLMs通常结合使用,以提高模型在解决数学问题上的性能。PLMs可以为模型提供对数学语言和结构的基础理解,而LLMs则可以处理更复杂的推理和计算任务。
通过这些模型,计算机不仅能够执行简单的数学计算,还能够解决复杂的数学问题,甚至生成和证明新的数学定理,这在数学教育和研究中具有巨大的潜力。
数学任务的自动化
MLMs能够处理的数学任务范围广泛,从基础的算术运算到复杂的定理证明。这些模型不仅能够理解数学问题,还能生成解题步骤和证明,极大地提高了解决问题的效率。
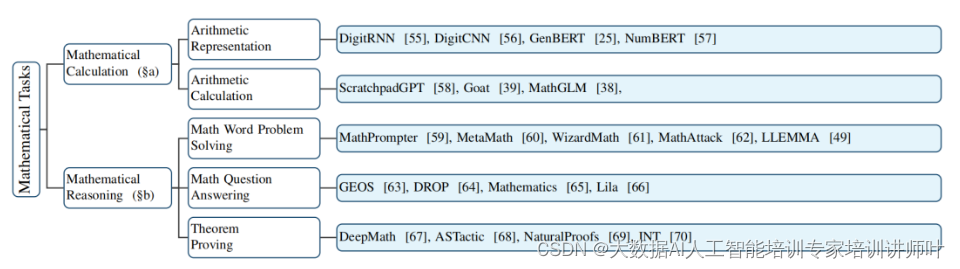
想象一下,计算机面前有一个问题:“一个教室里有3个学生,然后又进来了5个学生,现在教室里总共有多少个学生?”
-
理解问题:首先,计算机需要理解这个问题。它通过自然语言处理(NLP)技术来识别问题中的关键词和它们之间的关系。在这个例子中,关键词包括“学生”和数字“3”和“5”。
-
解析数学表达式:计算机将问题中的叙述转换为数学表达式。对于这个问题,表达式是“3 + 5”。
-
执行计算:接下来,计算机执行加法运算。这是一个直接的算术操作,计算机可以直接得出结果“8”。
-
生成答案:计算完成后,计算机生成答案并将其以文本形式输出。在这个例子中,输出是:“现在教室里总共有8个学生。”
这个过程可以扩展到更复杂的数学问题,如代数方程、微积分问题或几何证明。对于这些问题,计算机可能需要:
- 符号计算:使用符号数学库来处理未知数和抽象表达式。
- 逻辑推理:应用算法来解决逻辑谜题或证明定理。
- 机器学习:训练模型来识别问题中的模式,并预测解决方案。
此外,计算机还可以通过以下方式来提高其解决数学问题的能力:
- 链式思考(Chain-of-Thought):生成一系列逻辑步骤来解决复杂问题,模仿人类的思考过程。
- 工具辅助:集成计算器、符号求解器等工具来辅助计算。
- 自我修正:通过与外部工具的交互来验证和修正其答案。
数学任务的自动化不仅限于计算,它还包括教育应用,如自动评分学生作业、个性化学习推荐,以及在高级研究中辅助数学家发现新的理论和证明。
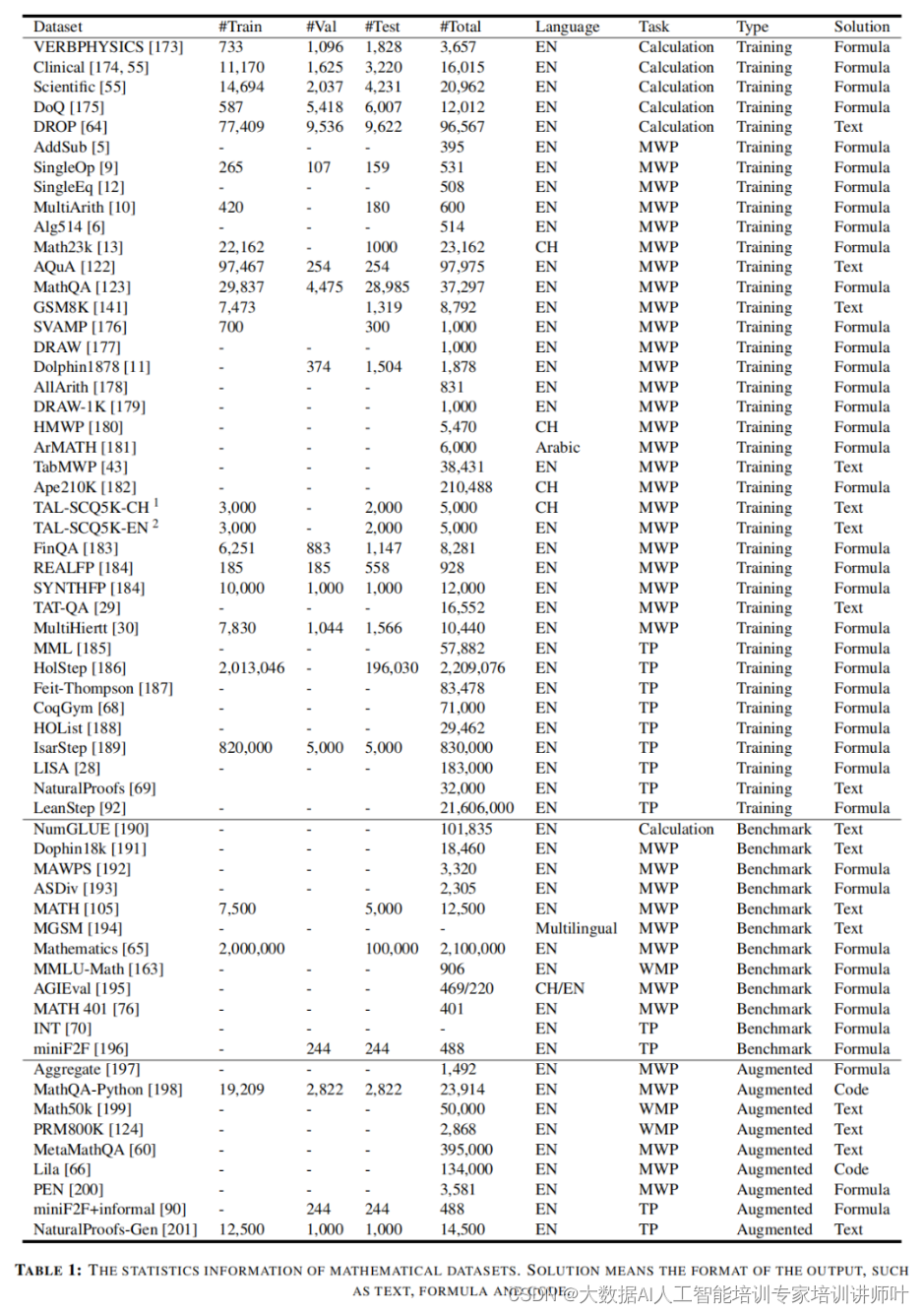
数据集的重要性
为了训练和评估MLMs的数学能力,研究者们设计了多种数学数据集。这些数据集被分为训练集、基准测试集和增强数据集,它们对于推动MLMs的研究和发展起到了关键作用。
尽管MLMs在数学问题解决上取得了显著进展,但它们仍面临着一系列挑战,包括输出的忠实度、多模态数据处理、不确定性处理、评估机制的建立、创造性定理的生成以及教育资源的稀缺性。
论文的链接:
https://arxiv.org/abs/2312.07622