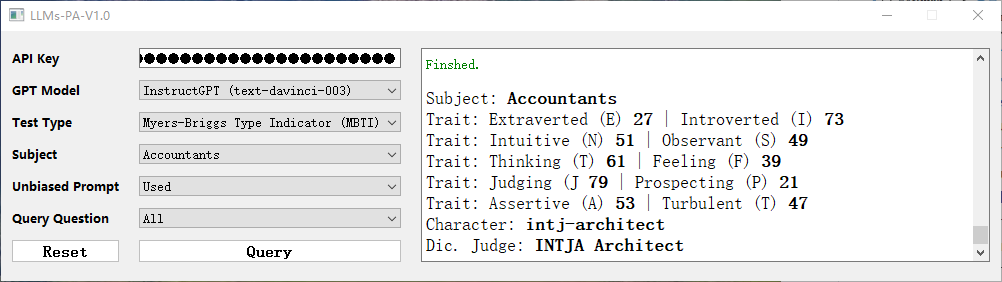
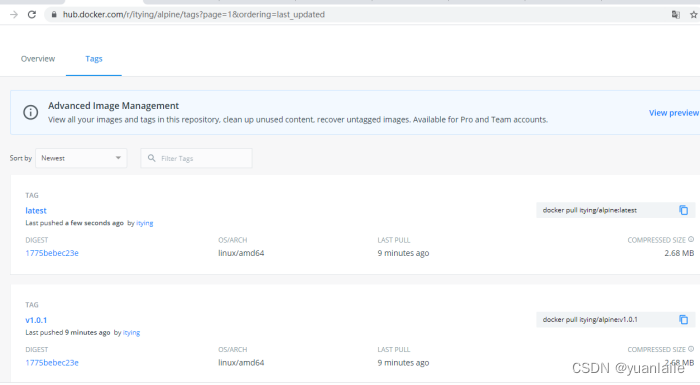
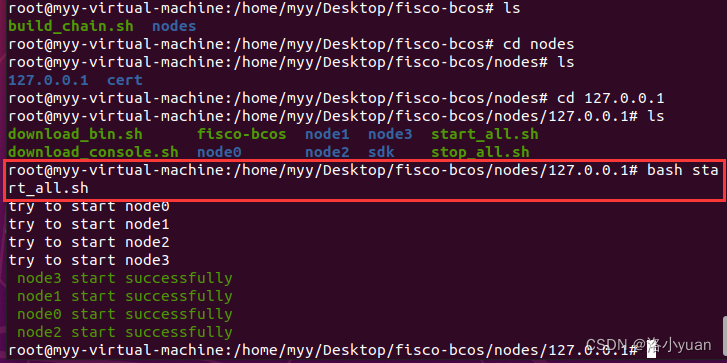
思路：

 其实就是图的拓扑排序，我们可以构建一个图形结构，比如[0,1]表示1->0，对于0来说入度为+1。

遍历结束后，从入度为0的开始遍历。引文只有入度为0的节点没有先决条件。然后依次减少1。直到所有节点入度都为0.然后记录下来count和需要学习课程数相比如果相等表示可以。不相等表示存在环。

class Solution {
   public static class Node {
        public int name;
        public int in;
        public ArrayList<Node> nexts;

        public Node(int n) {
            name = n;
            in = 0;
            nexts = new ArrayList<>();
        }
    }

    public static boolean canFinish(int numCourses, int[][] prerequisites) {
        if (prerequisites == null || prerequisites.length == 0) {
            return true;
        }
        Map<Integer, Node> nodes = new HashMap<>();
        for (int[] arr : prerequisites) {
            //目标课程编号
            int to = arr[0];
            //前驱课程编号
            int from = arr[1];
            if (!nodes.containsKey(to)) {
                nodes.put(to, new Node(to));
            }
            if (!nodes.containsKey(from)) {
                nodes.put(from, new Node(from));
            }
            //获取目标课程 节点
            Node t = nodes.get(to);
            Node f = nodes.get(from);
            //表示前驱课程指向目标课程  就是图的有向指标
            f.nexts.add(t);
            //目标课程入度++
            t.in++;
        }
        int needPrerequisiteNums = nodes.size();
        //建立一个入度为0 队列 表示这个是起始节点
        Queue<Node> zeroInQueue = new LinkedList<>();
        for (Node node : nodes.values()) {
            if (node.in == 0) {
                zeroInQueue.add(node);
            }
        }
        int count = 0;
        //拓扑排序  一次减少入度  如果count！=needPrerequisiteNums 说明有环，循环依赖 
        while (!zeroInQueue.isEmpty()) {
            Node cur = zeroInQueue.poll();
            count++;
            for (Node next : cur.nexts) {
                if (--next.in == 0) {
                    zeroInQueue.add(next);
                }
            }
        }
        return count == needPrerequisiteNums;
    }
}