活动 - AcWing
求给定区间 [X,Y] 中满足下列条件的整数个数:这个数恰好等于 K 个互不相等的 B 的整数次幂之和。
例如,设 X=15,Y=20,K=2,B=2,则有且仅有下列三个数满足题意:
17=24+20
18=24+21
20=24+22
输入格式
第一行包含两个整数 X 和 Y,接下来两行包含整数 K 和 B。
输出格式
只包含一个整数,表示满足条件的数的个数。
数据范围
1≤X≤Y≤2^31−1
1≤K≤20
2≤B≤10
输入样例:
15 20
2
2
输出样例:
3解析:
数位DP基本概念
数位:把一个数字按照个、十、百、千等等一位一位地拆开,关注它每一位上的数字。
如果拆的是 十进制数,那么每一位数字都是 0 ~ 9,其他进制可 类比 十进制。
数位 DP:用来解决一类特定问题,这种问题比较好辨认,一般具有这几个特征:
要求统计满足一定条件的数的数量(即,最终目的为计数)
这些条件经过转化后可以使用「数位」的思想去理解和判断
输入会提供一个数字区间(有时也只提供上界)来作为统计的限制
上界很大(比如 10^9),暴力枚举验证会超时
从题目中分析出 数位DP 的模型后,做法就非常的 套路化 了
题目要求 一段区间 内符合某些条件的数的个数,我们用 前缀和思想 转换为求两个 前缀区间 的问题
res[l,r]=res[1,r]−res[1,l−1]
接下来的问题就是统计答案。
统计答案可以选择 记忆化搜索,也可以选择 循环迭代递推。
为了不重不漏地统计所有不超过上限的答案,要 从高到低 枚举每一位
再考虑每一位都可以 填哪些数字,最后利用上述 前缀和思想 统计答案
记忆化搜索 中要引入的参数通常有:
1.当前枚举到的数位 pos(搜索的深度)
2.前一位数(或是前几位数)的情况 st(诸如 前一位是什么、前几位总和是多少、某个数出现了几次 等)
3.前几位的数字是否等于上界的前几位数字 op (0/1)限制本次搜索的数位范围)
4.是否有前导零 lead (0/1)
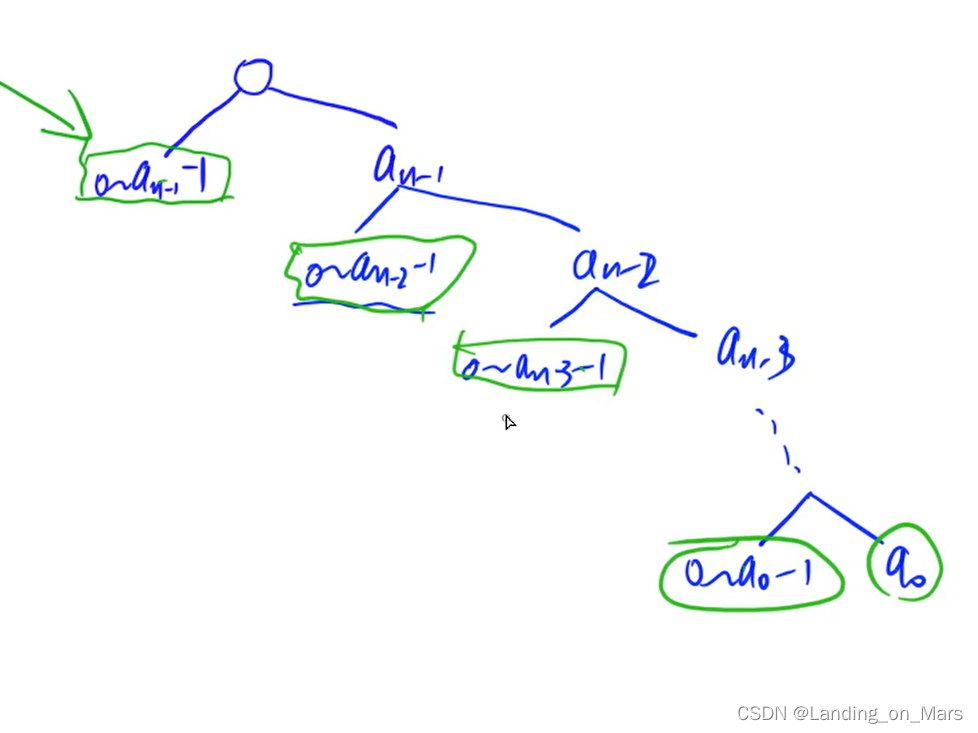
记忆化搜索的 递归搜索树 y总已经画过了,这里就不再额外绘制(本身也不复杂,就留给读者了)
循环迭代递推 的方法,大家可以看 y总 的 算法提高课 以及 lyd 的 蓝书 上的介绍
何时能用 记忆化搜索 优化掉当前搜索分支
当前 数位 能够枚举集合内所有元素的时候(没有贴着上界),即 !op
---------------------------------------------------------------------------------------------------------------------------------
作者:一只野生彩色铅笔
链接:https://www.acwing.com/solution/content/66855/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<double, double> PDD;
const int INF = 0x3f3f3f3f, mod = 1e9;
const double eps = 1e-8;
const int N = 35, M = N * 2;
int X, Y;
int K, B;
int c[N][N];
void init() {
for (int i = 0; i < N; i++) {
for (int j = 0; j <= i; j++) {
if (!j)c[i][j] = 1;
else c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
}
}
}
int dp(int n) {
if (!n)return 0;
vector<int>nums;
while (n)nums.push_back(n % B), n /= B;
int ret = 0;
int last = 0;
for (int i = nums.size() - 1; i >= 0; i--) {
int x = nums[i];
if (x) {
ret += c[i][K - last];
if (x > 1) {
if (K - last - 1 >= 0)ret += c[i][K - last - 1];
break;
}
else {
last++;
if (last > K)break;
}
}
if (!i && last == K)ret++;
}
return ret;
}
int main() {
init();
cin >> X >> Y;
cin >> K >> B;
cout << dp(Y) - dp(X - 1) << endl;
return 0;
}